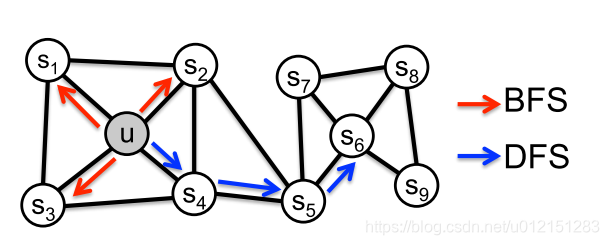
前面介绍过基于DFS邻域的DeepWalk和基于BFS邻域的LINE。

DeepWalk：算法原理，实现和应用
LINE：算法原理，实现和应用

node2vec是一种综合考虑DFS邻域和BFS邻域的graph embedding方法。简单来说，可以看作是eepwalk的一种扩展，可以看作是结合了DFS和BFS随机游走的deepwalk。

nodo2vec 算法原理

优化目标

设$f(u)$是将顶点$u$映射为embedding向量的映射函数,对于图中每个顶点$u$，定义$N_S(u)$为通过采样策略$S$采样出的顶点$u$的近邻顶点集合。

node2vec优化的目标是给定每个顶点条件下，令其近邻顶点出现的概率最大。

$ma{x}_f{\sum }_{u\in V}\log Pr(N_S(U)|f(u))$

为了将上述最优化问题可解，文章提出两个假设：

• 条件独立性假设
  假设给定源顶点下，其近邻顶点出现的概率与近邻集合中其余顶点无关。
  $Pr(N_s(u)|f(u))={\prod }_{n_i\in N_s(u)}Pr(n_i|f(u))$
• 特征空间对称性假设
  这里是说一个顶点作为源顶点和作为近邻顶点的时候共享同一套embedding向量。(对比LINE中的2阶相似度，一个顶点作为源点和近邻点的时候是拥有不同的embedding向量的)
  在这个假设下，上述条件概率公式可表示为$Pr(n_i|f(u))=\frac{\exp f(n_i)\cdot f(u)}{{\sum }_{v\in V}\exp f(v)\cdot f(u)}$

根据以上两个假设条件，最终的目标函数表示为
$ma{x}_f{\sum }_{u\in V}[-\log Z_u+{\sum }_{n_i\in N_s(u)}f(n_i)\cdot f(u)]$

由于归一化因子$Z_u={\sum }_{n_i\in N_s(u)}\exp (f(n_i)\cdot f(u))$的计算代价高，所以采用负采样技术优化。

采样策略

node2vec依然采用随机游走的方式获取顶点的近邻序列，不同的是node2vec采用的是一种有偏的随机游走。

给定当前顶点$v$，访问下一个顶点$x$的概率为
$$P(c_i=x|c_{i-1}=v)=\{\begin{array}{rlr}\frac{{\pi }_{vx}}{Z}& & \text{if }(v,x)\in E\\ 0& & \text{otherwise}\end{array}$$
${\pi }_{vx}$是顶点$v$和顶点$x$之间的未归一化转移概率，$Z$是归一化常数。

node2vec引入两个超参数$p$和$q$来控制随机游走的策略，假设当前随机游走经过边$(t,v)$到达顶点$v$
设${\pi }_{vx}={\alpha }_{pq}(t,x)\cdot w_{vx}$，$w_{vx}$是顶点$v$和$x$之间的边权，

$${\alpha }_{pq}(t,x)=\{\begin{array}{rlr}\frac{1}{p}& =& \text{if }{d}_{tx}=0\\ 1& =& \text{if }{d}_{tx}=1\\ \frac{1}{q}& =& \text{if }{d}_{tx}=2\end{array}$$
$d_{tx}$为顶点$t$和顶点$x$之间的最短路径距离。

下面讨论超参数$p$和$q$对游走策略的影响

• Return parameter,p
  参数$p$控制重复访问刚刚访问过的顶点的概率。
  注意到$p$仅作用于$d_{tx}=0$的情况，而$d_{tx}=0$表示顶点$x$就是访问当前顶点$v$之前刚刚访问过的顶点。
  那么若$p$较高，则访问刚刚访问过的顶点的概率会变低，反之变高。
• In-out papameter,q
  $q$控制着游走是向外还是向内，若q>1，随机游走倾向于访问和$t$接近的顶点(偏向BFS)。若$q<1$，倾向于访问远离$t$的顶点(偏向DFS)。

下面的图描述的是当从t访问到v时，决定下一个访问顶点时每个顶点对应的$\alpha$。

学习算法

采样完顶点序列后，剩下的步骤就和deepwalk一样了，用word2vec去学习顶点的embedding向量。
值得注意的是node2vecWalk中不再是随机抽取邻接点，而是按概率抽取，node2vec采用了Alias算法进行顶点采样。
Alias Method:时间复杂度O(1)的离散采样方法

node2vec核心代码

node2vecWalk

通过上面的伪代码可以看到，node2vec和deepwalk非常类似，主要区别在于顶点序列的采样策略不同，所以这里我们主要关注node2vecWalk的实现。

由于采样时需要考虑前面2步访问过的顶点，所以当访问序列中只有1个顶点时，直接使用当前顶点和邻居顶点之间的边权作为采样依据。
当序列多余2个顶点时，使用文章提到的有偏采样。

def node2vec_walk(self, walk_length, start_node):G = self.G    alias_nodes = self.alias_nodes    alias_edges = self.alias_edgeswalk = [start_node]while len(walk) < walk_length:        cur = walk[-1]        cur_nbrs = list(G.neighbors(cur))        if len(cur_nbrs) > 0:            if len(walk) == 1:                walk.append(cur_nbrs[alias_sample(alias_nodes[cur][0], alias_nodes[cur][1])])            else:                prev = walk[-2]                edge = (prev, cur)                next_node = cur_nbrs[alias_sample(alias_edges[edge][0],alias_edges[edge][1])]                walk.append(next_node)        else:            breakreturn walk

构造采样表

preprocess_transition_probs分别生成alias_nodes和alias_edges，alias_nodes存储着在每个顶点时决定下一次访问其邻接点时需要的alias表（不考虑当前顶点之前访问的顶点）。alias_edges存储着在前一个访问顶点为$t$，当前顶点为$v$时决定下一次访问哪个邻接点时需要的alias表。

get_alias_edge方法返回的是在上一次访问顶点$t$，当前访问顶点为$v$时到下一个顶点$x$的未归一化转移概率${\pi }_{vx}={\alpha }_{pq}(t,x)\cdot w_{vx}$

def get_alias_edge(self, t, v):G = self.G    p = self.p    q = self.qunnormalized_probs = []    for x in G.neighbors(v):        weight = G[v][x].get('weight', 1.0)# w_vx        if x == t:# d_tx == 0            unnormalized_probs.append(weight/p)        elif G.has_edge(x, t):# d_tx == 1            unnormalized_probs.append(weight)        else:# d_tx == 2            unnormalized_probs.append(weight/q)    norm_const = sum(unnormalized_probs)    normalized_probs = [float(u_prob)/norm_const for u_prob in unnormalized_probs]return create_alias_table(normalized_probs)def preprocess_transition_probs(self):G = self.Galias_nodes = {}    for node in G.nodes():        unnormalized_probs = [G[node][nbr].get('weight', 1.0) for nbr in G.neighbors(node)]        norm_const = sum(unnormalized_probs)        normalized_probs = [float(u_prob)/norm_const for u_prob in unnormalized_probs]                 alias_nodes[node] = create_alias_table(normalized_probs)alias_edges = {}for edge in G.edges():        alias_edges[edge] = self.get_alias_edge(edge[0], edge[1])self.alias_nodes = alias_nodes    self.alias_edges = alias_edgesreturn

node2vec应用

使用node2vec在wiki数据集上进行节点分类任务和可视化任务。 wiki数据集包含 2,405 个网页和17,981条网页之间的链接关系，以及每个网页的所属类别。 通过简单的超参搜索，这里使用p=0.25,q=4的设置。

本例中的训练，评测和可视化的完整代码在下面的git仓库中，

https://github.com/shenweichen/GraphEmbedding

G = nx.read_edgelist('../data/wiki/Wiki_edgelist.txt',create_using=nx.DiGraph(),nodetype=None,data=[('weight',int)])model = Node2Vec(G,walk_length=10,num_walks=80,p=0.25,q=4,workers=1)
model.train(window_size=5,iter=3)    
embeddings = model.get_embeddings()evaluate_embeddings(embeddings)
plot_embeddings(embeddings)

分类任务

micro-F1: 0.6757
macro-F1: 0.5917

这个结果相比于DeepWalk和LINE是有提升的。

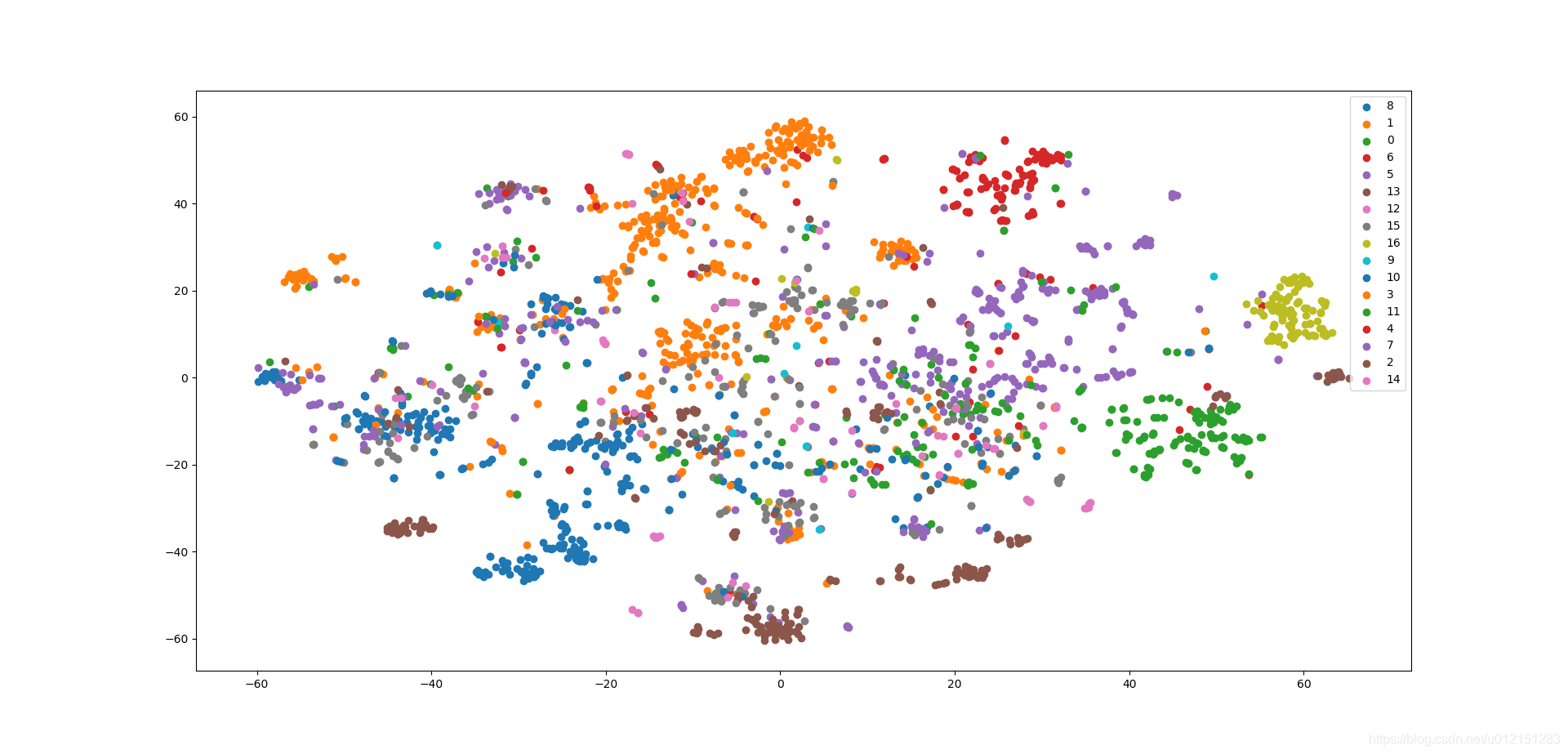
可视化

这个结果相比于DeepWalk和LINE可以看到不同类别的分布更加分散了。

参考资料

• Grover A, Leskovec J. node2vec: Scalable Feature Learning for Networks[C]// Acm Sigkdd International Conference on Knowledge Discovery & Data Mining. 2016.

图算法干货汇总

我把近年来主流的图表示学习方法的paper和对应的代码实现进行了汇总整理，扫码关注公众号【浅梦的学习笔记】，后台回复【图算法】即可打包下载。

欢迎加入星球群，一个由1300+小伙伴共建的交流平台，专注于前沿graph embedding算法技术与实践经验的分享学习。