算法 字符串匹配之朴素算法和KMP算法及JAVA代码实现
2017年06月02日 10:31:12
阅读数:941
暴力匹配算法
假设现在我们面临这样一个问题:有一个文本串S,和一个模式串P,现在要查找P在S中的位置,怎么查找呢?
如果用暴力匹配的思路,并假设现在文本串S匹配到 i 位置,模式串P匹配到 j 位置,则有:
-
如果当前字符匹配成功(即S[i] == P[j]),则i++,j++,继续匹配下一个字符;
-
如果失配(即S[i]! = P[j]),令i = i - (j - 1),j = 0。相当于每次匹配失败时,i 回溯,j 被置为0。
example:
如果给定文本串S“BBC ABCDAB ABCDABCDABDE”,和模式串P“ABCDABD”,现在要拿模式串P去跟文本串S匹配,整个过程如下所示:
- S[0]为B,P[0]为A,不匹配,模式串要往右移动一位

2. S[1]跟P[0]还是不匹配,模式串继续右移

3.直到S[4]跟P[0]匹配成功(i=4,j=0)此时比较两个字符串的下一个字符

4. 匹配成功 继续比较两个字符串的下一个字符

5. 直到S[10]为空格字符,P[6]为字符D(i=10,j=6),因为不匹配,将模式串右移一位继续比较

6. 继续按照上述方法进行比较
JAVA代码实现
/*** 暴力匹配算法** @param sStr 父串* @param dStr 子串* @return 子串在父串中下标index[int]*/public static int violentMatch(String sStr, String dStr) {int sLength = sStr.length();int dLength = dStr.length();int sIndex = 0, dIndex = 0;while (sIndex < sLength && dIndex < dLength) {//当前字符匹配if (sStr.charAt(sIndex) == dStr.charAt(dIndex)) {//父串和子串同时后移一个字符sIndex++;dIndex++;} else {//不匹配则sIndex回溯,dIndex被置为0sIndex = sIndex - (dIndex - 1);dIndex = 0;}}if (dIndex == dLength) {return sIndex - dLength;}return -1;}测试一下
/*测试数据*/String onceStr = "eeeabceee";String noneStr = "adfsdf";String mutiStr1 = "eeeeeeabceeeabc";String mutiStr2 = "eeeeeeabceeeabc";String destStr = "abc";String replaceStr = "XXX";/*输出格式*/String indexPattern = "{0} 在 {1} 首次出现的位置: {2}";String indexesPattern = "{0} 在 {1} 出现的所有位置:{2}";String replacePattern = "使用 {0} 替换 {1} 中的 {2}: {3}";/*===========测试暴力匹配算法===========*///1.测试出现一次情况index = StringMatcher.violentMatch(onceStr, destStr);System.out.println(MessageFormat.format(indexPattern, destStr, onceStr, index));//2.测试出现多次情况index = StringMatcher.violentMatch(mutiStr1, destStr);System.out.println(MessageFormat.format(indexPattern, destStr, mutiStr1, index));输出结果
abc 在 eeeabceee 首次出现的位置: 3
abc 在 eeeeeeabceeeabc 首次出现的位置: 6
- 1
- 2
- 3
KMP算法
KMP的算法流程:
假设现在文本串S匹配到 i 位置,模式串P匹配到 j 位置
-
如果j = -1,或者当前字符匹配成功(即S[i] == P[j]),都令i++,j++,继续匹配下一个字符;
-
如果j != -1,且当前字符匹配失败(即S[i] != P[j]),则令 i 不变,j = next[j]。此举意味着失配时,模式串P相对于文本串S向右移动了j - next [j] 位。
换言之,当匹配失败时,模式串向右移动的位数为:失配字符所在位置 - 失配字符对应的next 值(next 数组的求解会在下文的3.3.3节中详细阐述),即移动的实际位数为:j - next[j],且此值大于等于1。
很快,你也会意识到next 数组各值的含义:代表当前字符之前的字符串中,有多大长度的相同前缀后缀。例如如果next [j] = k,代表j 之前的字符串中有最大长度为k 的相同前缀后缀。
此也意味着在某个字符失配时,该字符对应的next 值会告诉你下一步匹配中,模式串应该跳到哪个位置(跳到next [j] 的位置)。如果next [j] 等于0或-1,则跳到模式串的开头字符,若next [j] = k 且 k > 0,代表下次匹配跳到j 之前的某个字符,而不是跳到开头,且具体跳过了k 个字符。
转换成JAVA代码就是
/*** KMP匹配算法** @param sStr 父串* @param dStr 子串* @return 子串在父串中下标index[int]*/public static int KMPMatch(String sStr, String dStr) {int sLength = sStr.length();int dLength = dStr.length();int sIndex = 0, dIndex = 0;int[] next = getNextArray(dStr);while (sIndex < sLength && dIndex < dLength) {//当前字符匹配if (dIndex==-1||sStr.charAt(sIndex) == dStr.charAt(dIndex)) {//父串和子串同时后移一个字符sIndex++;dIndex++;} else {//不匹配 sIndex不变dIndex取next[j]dIndex = next[dIndex];}}if (dIndex == dLength) {return sIndex - dLength;}return -1;}问题的关键是如何求next数组
求解next数组
- 寻找前缀后缀最长公共元素长度
如果给定的模式串为“abab”,那么它的各个子串的前缀后缀的公共元素的最大长度如下表格所示:
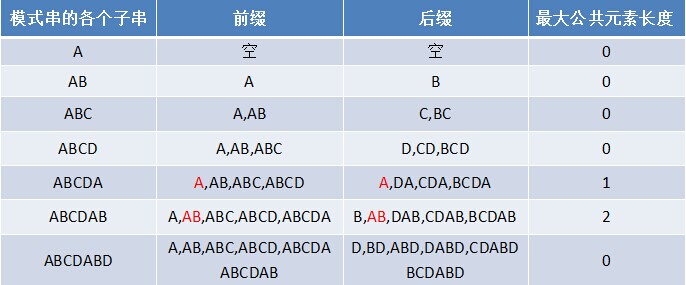
如果给定的模式串是:“ABCDABD”,从左至右遍历整个模式串,其各个子串的前缀后缀分别如下表格所示:
- 求next数组
next 数组考虑的是除当前字符外的最长相同前缀后缀,所以通过第①步骤求得各个前缀后缀的公共元素的最大长度后,只要稍作变形即可:将第①步骤中求得的值整体右移一位,然后初值赋为-1,如下表格所示:
对于给定的模式串:ABCDABD,它的最大长度表及next 数组分别如下:
JAVA代码实现
/*** 获取next数组** @param destStr 目的字符串* @return next数组*/public static int[] getNextArray(String destStr) {int[] nextArr = new int[destStr.length()];nextArr[0] = -1;int k = -1, j = 0;while (j < destStr.length() - 1) {if (k == -1 || (destStr.charAt(j) == destStr.charAt(k))) {++k;++j;nextArr[j] = k;} else {k = nextArr[k];}}return nextArr;}测试
/*===========测试KMP匹配算法===========*/
index = StringMatcher.KMPMatch(onceStr, destStr); System.out.println(MessageFormat.format(indexPattern, destStr, onceStr, index)); index = StringMatcher.violentMatch(mutiStr1, destStr); System.out.println(MessageFormat.format(indexPattern, destStr, mutiStr1, index));
测试结果
abc 在 eeeabceee 首次出现的位置: 3
abc 在 eeeeeeabceeeabc 首次出现的位置: 6