- 利用对称正定矩阵的乔累斯基分解求解对称正定方程组的方法称为平方根法
- 对称正定矩阵A的对角元为正
- 实对称矩阵A正定的充要条件是A的所有特征值为正
- 对称正定矩阵非奇异,其逆亦为对称正定矩阵
- 实对称矩阵A正定的充要条件是A的所有顺序主子式为正
- 正定矩阵的顺序主子阵是正定的
- Cholesky分解较一般的LU分解乘除法计算量小得多。它所需要的乘除次数约为(n^3)/6数量级,差不多比LU分解节省一半的工作量,但要进行n次开方运算
- (比高斯法更稳定,不需要选主元)
%% 0.平方根法解线性方程组,输出L矩阵和根
%% 1.对称正定矩阵的Cholesky分解
%对称正定矩阵A存在唯一的对角元素均为正数的下三角矩阵L,使得A=L*L(转置)
%这种分解叫做Cholesky分解
A=[3,3,5;3,5,9;5,9,17];
b=[0;-2;-4];
%判断矩阵A是否对称正定,对称+所有顺序主子式为正
L=zeros(3);
%求下三角矩阵L
L(1,1)=sqrt(A(1,1));%L11
L(2,1)=A(2,1)/L(1,1);%L21
L(3,1)=A(3,1)/L(1,1);%L31
L(2,2)=sqrt(A(2,2)-L(2,1)*L(2,1));%L22
L(3,2)=(A(3,2)-L(3,1)*L(2,1))/L(2,2);%L32
L(3,3)=sqrt(A(3,3)-L(3,1)*L(3,1)-L(3,2)*L(3,2));%L33
L%输出L矩阵
%% 2.由Ly=b得到y
y=L\b;
%% 3.由L_转置*x=y得到方程组的解x
x=L'\y%输出线性方程组的根
运行结果:

其中y矩阵:
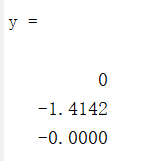
利用MATLAB内置函数chol
%% 0.平方根法解线性方程组,输出L矩阵和根
%% 1.对称正定矩阵的Cholesky分解
%对称正定矩阵A存在唯一的对角元素均为正数的下三角矩阵L,使得A=L*L'
%这种分解叫做Cholesky分解
A=[3,3,5;3,5,9;5,9,17];
b=[0;-2;-4];
%L=chol(A,'lower')基于矩阵A的对角线和下三角形生成下三角矩阵L,满足方程L*L'=A
L=chol(A,'lower')
%% 2.由Ly=b得到y
y=L\b;
%% 3.由L_转置*x=y得到方程组的解x
x=L'\y%输出线性方程组的根
如果矩阵A不是对称的,则 chol 使用上三角的(复共轭)转置作为下三角。