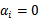目录

两个必须的知识点

字节码指令验证

结果分析

非法前向引用变量

---

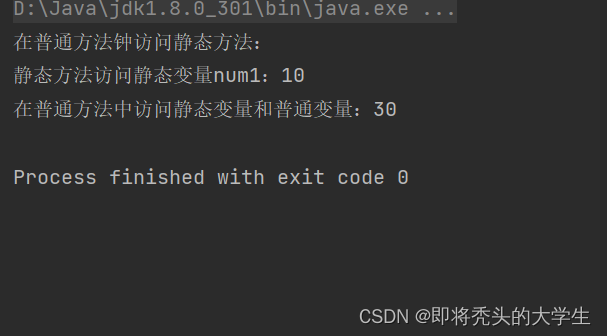
        最近在学JVM，在学到类的初始化的时候明白了以前不是很理解的类中静态变量的初始化的过程，如果你也对静态变量的初始化有所困扰或者如下图的输出结果有所疑惑，相信你看完本文，一定会有所帮助。

        

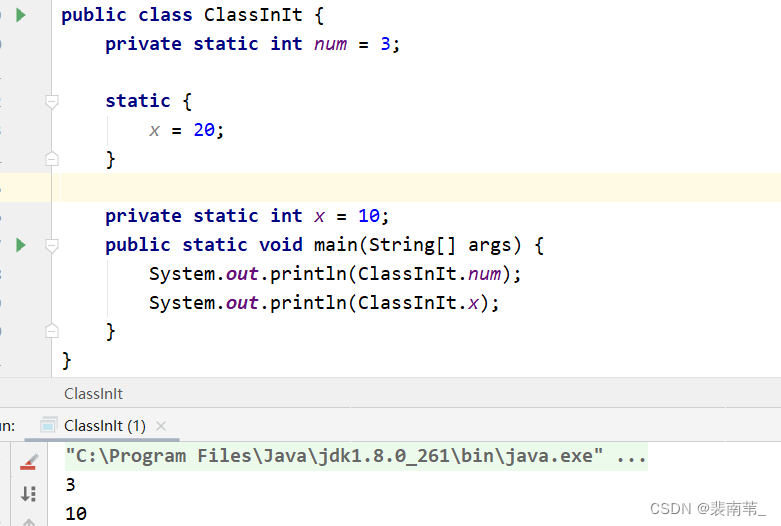
两个必须的知识点

首先在讲解上图的内容的前，我们需要明白两个知识点。

        在类加载过程中准备阶段，java虚拟机会给类变量赋予初始值，也就是0值。

所谓0值，也就是 0，null，false。int类型赋值为0，引用类型赋值为null，布尔类型赋值为false

        类的初始化阶段是类加载过程中的最后一个步骤。

        在前面的类初始化阶段中的准备(prepare)阶段中已经给类变量进行赋予初始值(0值)，所以到了初始化阶段，会根据程序员通过程序编码指定的主观计划去初始化类变量和其他资源。

        我们也可以从另外一种更直接的形式来表达：初始化阶段就是执行类构造器clinit()方法的过程。clinit()并不是程序员在Java代码中直接编写的方法，它是Javac编译器的自动生成物.

        通俗来讲，到了初始化阶段，静态变量也就被赋予我们规定的值了。、

字节码指令验证

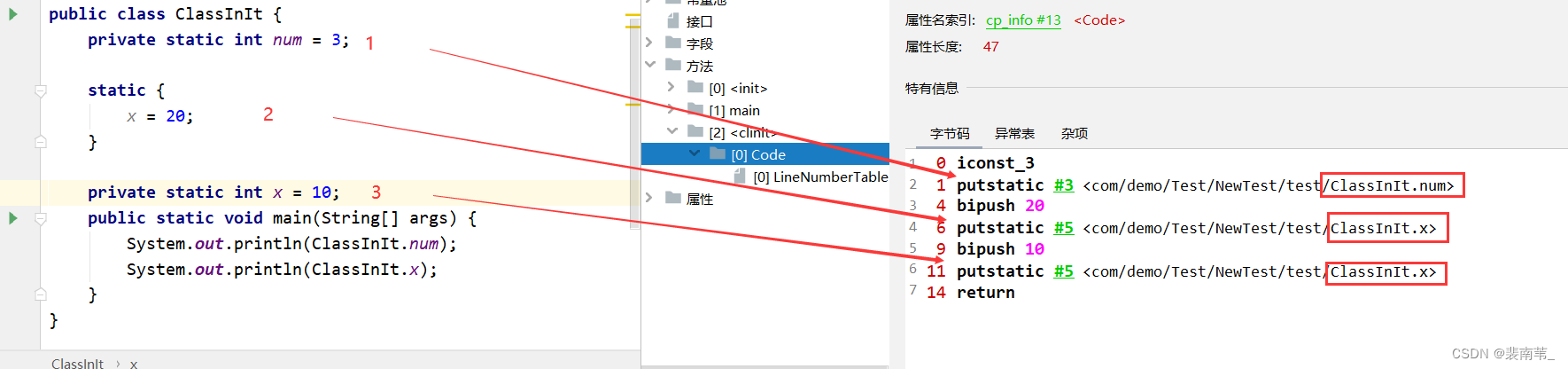
可以查看下图所示的例子，方便理解

        我们可以通过jclasslib查看字节码指令

JVM中 int 类型数值，根据 取值范围将 入栈的 字节码指令 就分为4类：

取值 -1~5 采用 iconst 指令；

取值 -128~127 采用 bipush 指令；

取值 -32768~32767 采用 sipush指令；

取值 -2147483648~2147483647 采用 ldc 指令。

不知道怎么查看字节码指令的朋友查看这里：

Idea中jclasslib的安装与使用_裴南苇_的博客-CSDN博客

结果分析

①由于在准备阶段，已经对类的静态变量赋予初始值，所以这里直接对x赋值不会报错(但是不能进行引用)，这也就引出了下一个问题：非法前向引用变量。

②在初始化阶段，编译器收集的顺序是由语句在源文件中出现的顺序决定的。我们知道这一点之后，静态块中x被赋值20是先出现的，所以对应右面的jclasslib先赋值20，然后再被10覆盖，所以打印为10.

非法前向引用变量

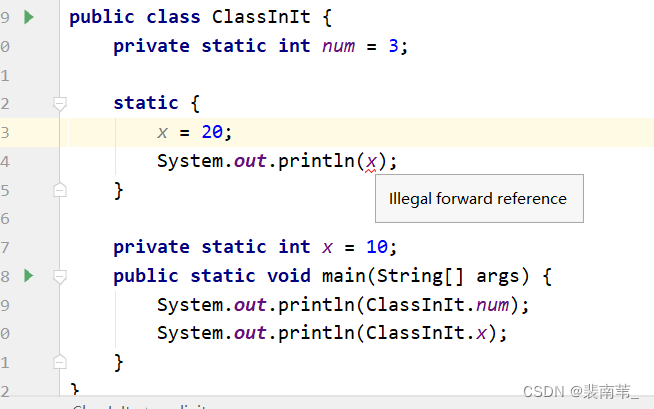
        虚拟机规定：静态语句块中只能访问到定义在静态语句块之前的变量，定义在它之后的变量，在前面的静态语句块可以赋值，但是不能访问。

        所以下图的例子会编译失败。这也就是非法前向引用变量

好了，这次的文章就到这里，喜欢的同学可以点赞收藏，遇到问题，可以评论，或者留言，我一定会第一时间给到回馈，感谢观看！！

注：本文为本人学习时心得分享，有讲错或者需要改正的地方，请指正，我会虚心接受