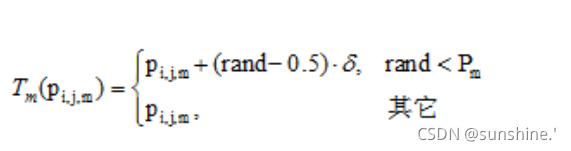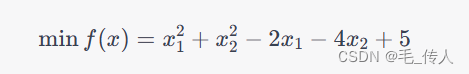免疫算法理论
生物免疫系统是-一个复杂的自适应系统。免疫系统能够识别出病原体,具有学习、记忆和模式识别能力,因此可以借鉴其信息处理机制来解决科学和工程问题。免疫算法正是基于生物免疫系统识别外部病原体并产生抗体对抗病原体的学习机制而提出的,由此诞生了基于免疫原理的智能优化方法研究这一新的研究方向。
生物免疫系统
传统免疫是指机体抗感染的防御能力,而现代免疫则指机体免疫系统识别和排除抗原性异物,从而维持机体生理平衡和稳定的功能。免疫是机体的一种生理反应,当病原体(即抗原)进入人体时,这些抗原将刺激免疫细胞(淋巴B细胞、T细胞)产生一种抵抗该病原生物的特殊蛋白质- --抗体。抗体能将该病原生物消灭,并在将病原生物消灭之后,仍存留在人体内。当同样的病原生物再次侵入人体时,该病原生物就会很快地被体内存留的抗体消灭。
免疫
免疫是指机体对自身和异体识别与响应过程中产生的生物学效应的总和,正常情况下是一种维持机体循环稳定的生理性功能。生物机体识别异体抗原,对其产生免疫响应并清除;机体对自身抗原不产生免疫响应。
抗原
抗原是一种能够刺激机体产生免疫应答并能与应答产物结合的物质。它不是免疫系统的有机组成部分,但它是启动免疫应答的始动因素。
抗体
抗体是一种能够进行特异识别和清除抗原的免疫分子,其中具有抗细菌和抗毒素免疫功能的球蛋白物质,故抗体也称免疫球蛋白分子,它是由B细胞分化成的浆细胞所产生的。
T细胞和B细胞
T细胞和B细胞是淋巴细胞的主要组成部分。B细胞受到抗原刺激后,可增殖分化为大量浆细胞,而浆细胞具有合成和分泌抗体的功能。但是,B细胞不能识别大多数抗原,必须借助能识别抗原的辅助性T细胞来辅助B细胞活化,产生抗体。
生物免疫系统原理
生物免疫系统是由免疫分子、免疫组织和免疫细胞组成的复杂系统。这些组成免疫系统的组织和器官分布在人体各处,用来完成各种免疫防卫功能,它们就是人们熟知的淋巴器官和淋巴组织。
免疫算法基本概念
免疫算法是受生物免疫系统的启发而推出的一种新型的智能搜索算法。它是一种确定性和随机性选择相结合并具有“勘探”与“开采”能力的启发式随机搜索算法。免疫算法将优化问题中待优化的问题对应免疫应答中的抗原,可行解对应抗体(B细胞),可行解质量对应免疫细胞与抗原的亲和度。如此则可以将优化问题的寻优过程与生物免疫系统识别抗原并实现抗体进化的过程对应起来,将生物免疫应答中的进化过程抽象为数学上的进化寻优过程,形成一种智能优化算法。
免疫算法是对生物免疫系统机理抽象而得的,算法中的许多概念和算子与免疫系统中的概念和免疫机理存在着对应关系。免疫算法与生物免疫系统概念的对应关系如表4.1所示。由于抗体是由B细胞产生的,在免疫算法中对抗体和B细胞不做区分,都对应为优化问题的可行解。

免疫算法的特点
免疫算法是受免疫学启发,模拟生物免疫系统功能和原理来解决复杂问题的自适应智能系统,它保留了生物免疫系统所具有的若干特,包括:
(1)全局搜索能力。模仿免疫应答过程提出的免疫算法是一 种具有全局搜索能力的优化算法,免疫算法在对优质抗体邻域进行局部搜索的同时利用变异算子和种群刷新算子不断产生新个体,探索可行解区间的新区域,保证算法在完整的可行解区间进行搜索,具有全局收敛性能。
(2)多样性保持机制。免疫算法借鉴了生物免疫系统的多样性保持机制,对抗体进行浓度计算,并将浓度计算的结果作为评价抗体个体优劣的-一个重要标准;它使浓度高的抗体被抑制,保证抗体种群具有很好的多样性,这也是保证算法全局收敛性能的一个重要方面。
(3)鲁棒性强。基于生物免疫机理的免疫算法不针对特定问题,而且不强调算法参数设置和初始解的质量,利用其启发式的智能搜索机制,即使起步于劣质解种群,最终也可以搜索到问题的全局最优解,对问题和初始解的依赖性不强,具有很强的适应性和鲁棒性。
(4)并行分布式搜索机制。免疫算法不需要集中控制,可以实现并行处理。而且,免疫算法的优化进程是一种多进程的并行优化,在探求问题最优解的同时可以得到问题的多个次优解,即除找到问题的最佳解决方案外,还会得到若干较好的备选方案,尤其适合于多模态的优化问题。
免疫算法算子
与遗传算法等其他智能优化算法类似,免疫算法的进化寻优过程也是通过算子来实现的。免疫算法的算子包括:亲和度评价算子、抗体浓度评价算子、激励度计算算子、免疫选择算子、克隆算子、变异算子、克隆抑制算子和种群刷新算子等。由于算法的编码方式可能为实数编码、离散编码等,不同编码方式下的算法算子会有所不同
亲和度评价算子
亲和度表征免疫细胞与抗原的结合强度,与遗传算法中的适应度类似。亲和度评价算子通常是一个函数aff(x): S∈R,其中S为问题的可行解区间,R为实数域。函数的输入为一个抗体个体(可行解),输出即为亲和度评价结果。亲和度的评价与问题具体相关,针对不同的优化问题,应该在理解问题实质的前提下,根据问题的特点定义亲和度评价函数。通常函数优化问题可以用函数值或对函数值的简单处理(如取倒数、相反数等)作为亲和度评价,而对于组合优化问题或应用中更为复杂的优化问题,则需要具体问题具体分析。
抗体浓度评价算子
抗体浓度表征抗体种群的多样性好坏。抗体浓度过高意味着种群中非常类似的个体大量存在,则寻优搜索会集中于可行解区间的一一个区域,不利于全局优化。因此优化算法中应对浓度过高的个体进行抑制,保证个体的多样性。
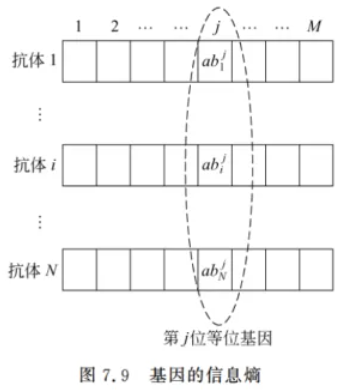
抗体浓度通常定义为:浓度越低值越大

进行抗体浓度评价的–个前提是抗体间亲和度的定义。免疫中经常提到的亲和度为抗体对抗原的亲和度,实际上抗体和抗体之间也存在着亲和度的概念,它代表了两个抗体个体之间的相似程度。抗体间亲和度的计算方法主要包括基于抗体和抗原亲和度的计算方法、基于欧氏距离的计算方法、基于海明距离的计算方法、基于信息熵的计算方法等。
对于实数编码的算法,抗体间亲和度通常可以通过抗体向量之间的欧氏距离来计算:

对于基于离散编码的算法,衡量抗体_抗体亲和度最直接的方法就是利用抗体串的海明距离:

激励度计算算子
抗体激励度是对抗体质量的最终评价结果,需要综合考虑抗体亲和度和抗体浓度,通常亲和度大(目标函数值好)、浓度低的抗体会得到较大的激励度(即优秀)。抗体激励度的计算通
常可以利用抗体亲和度和抗体浓度的评价结果进行简单的数学运算得到,如:

免疫选择算子
免疫选择算子根据抗体的激励度确定选择哪些抗体进入克隆选择操作。在抗体群中激励度高的抗体个体具有更好的质量,更有可能被选中进行克隆选择操作,在搜索空间中更有搜索价值。
克隆算子
克隆算子将免疫选择算子选中的抗体个体进行复制。,
变异算子
变异算子对克隆算子得到的抗体克隆结果进行变异操作,以产生亲和度突变,实现局部搜索。变异算子是免疫算法中产生有潜力的新抗体、实现区域搜索的重要算子,它对算法的性能有很大影响。变异算子也和算法的编码方式相关,实数编码的算法和离散编码的算法采用不同的变异算子。


克隆抑制算子
克隆抑制算子用于对经过变异后的克隆体进行再选择,抑制亲和度低的抗体,保留亲和度高的抗体进入新的抗体种群。在克隆抑制的过程中,克隆算子操作的源抗体与克隆体经变异算子作用后得到的临时抗体群共同组成-一个合,克隆抑制操作将保留此集合中亲和度最高的抗体,抑制其他抗体。由于克隆变异算子操作的源抗体是种群中的优质抗体,而克隆抑制算子操作的临时抗体集合中又包含了父代的源抗体,因此在免疫算法的算子操作中隐含了最优个体保留机制。
种群刷新算子
种群刷新算子用于对种群中激励度较低的抗体进行刷新,从抗体种群中删除这些抗体并以随机生成的新抗体替代,有利于保持抗体的多样性,实现全局搜索,探索新的可行解空间区域。
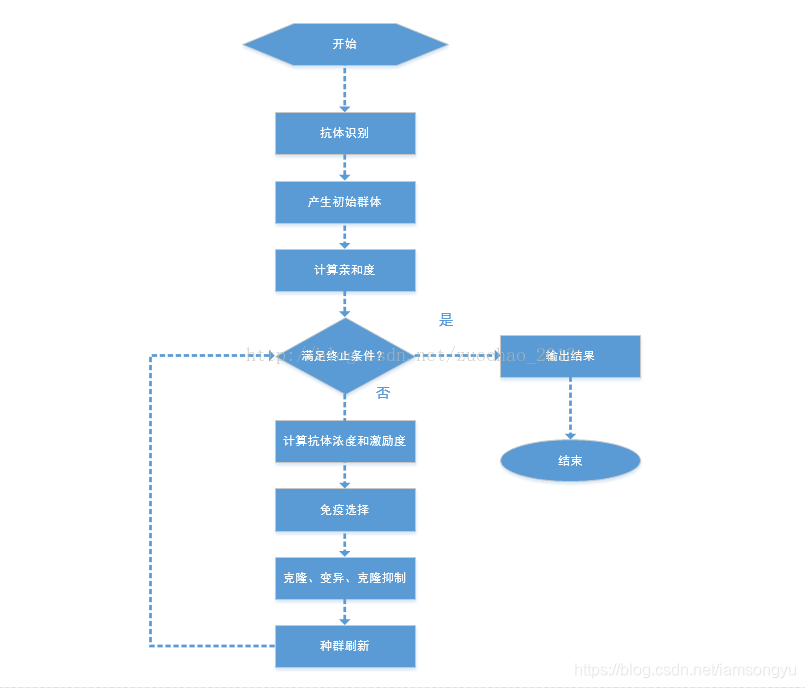
免疫算法流程

免疫算法算例
算例1
求函数f(x,y)= 5sin(x)+x2+y的最小值,其中x的取值范围为[-4, 4],y的取值范围为[-_4,4]。这是一个有多个局部极值的函数。
matlab求解
%%%%%%%%%%%%%%%%%免疫算法求函数极值%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%%%%%%%%
clear all; %清除所有变量
close all; %清图
clc; %清屏
D=2; %免疫个体维数
NP=50; %免疫个体数目
Xs=4; %取值上限
Xx=-4; %取值下限
G=200; %最大免疫代数
pm=0.7; %变异概率
alfa=2; %激励度系数
belta=1; %激励度系数
detas=0.2; %相似度阈值
gen=0; %免疫代数
Ncl=5; %克隆个数
deta0=0.5*Xs; %邻域范围初值
%%%%%%%%%%%%%%%%%%%%%%%初始种群%%%%%%%%%%%%%%%%%%%%%%%%
f=rand(D,NP)*(Xs-Xx)+Xx;
for np=1:NPMSLL(np)=func2(f(:,np));
end
%%%%%%%%%%%%%%%%%计算个体浓度和激励度%%%%%%%%%%%%%%%%%%%
for np=1:NPfor j=1:NP nd(j)=sum(sqrt((f(:,np)-f(:,j)).^2));if nd(j)<detasnd(j)=1;elsend(j)=0;endendND(np)=sum(nd)/NP;
end
MSLL = alfa*MSLL- belta*ND;
%%%%%%%%%%%%%%%%%%%激励度按升序排列%%%%%%%%%%%%%%%%%%%%%%
[SortMSLL,Index]=sort(MSLL);
Sortf=f(:,Index);
%%%%%%%%%%%%%%%%%%%%%%%%免疫循环%%%%%%%%%%%%%%%%%%%%%%%%
while gen<Gfor i=1:NP/2%%%%%%%%选激励度前NP/2个体进行免疫操作%%%%%%%%%%%a=Sortf(:,i);Na=repmat(a,1,Ncl);deta=deta0/gen;for j=1:Nclfor ii=1:D%%%%%%%%%%%%%%%%%变异%%%%%%%%%%%%%%%%%%%if rand<pmNa(ii,j)=Na(ii,j)+(rand-0.5)*deta;end%%%%%%%%%%%%%%边界条件处理%%%%%%%%%%%%%%%if (Na(ii,j)>Xs) | (Na(ii,j)<Xx)Na(ii,j)=rand * (Xs-Xx)+Xx;endendendNa(:,1)=Sortf(:,i); %保留克隆源个体%%%%%%%%%%克隆抑制,保留亲和度最高的个体%%%%%%%%%%for j=1:NclNaMSLL(j)=func2(Na(:,j));end[NaSortMSLL,Index]=sort(NaMSLL);aMSLL(i)=NaSortMSLL(1);NaSortf=Na(:,Index);af(:,i)=NaSortf(:,1);end %%%%%%%%%%%%%%%%%%%%免疫种群激励度%%%%%%%%%%%%%%%%%%%for np=1:NP/2for j=1:NP/2nda(j)=sum(sqrt((af(:,np)-af(:,j)).^2)); if nda(j)<detasnda(j)=1;elsenda(j)=0;endendaND(np)=sum(nda)/NP/2;endaMSLL = alfa*aMSLL- belta*aND;%%%%%%%%%%%%%%%%%%%%%%%种群刷新%%%%%%%%%%%%%%%%%%%%%%%bf=rand(D,NP/2)*(Xs-Xx)+Xx;for np=1:NP/2bMSLL(np)=func2(bf(:,np));end%%%%%%%%%%%%%%%%%%%新生成种群激励度%%%%%%%%%%%%%%%%%%%%for np=1:NP/2for j=1:NP/2ndc(j)=sum(sqrt((bf(:,np)-bf(:,j)).^2));if ndc(j)<detasndc(j)=1;elsendc(j)=0;endendbND(np)=sum(ndc)/NP/2;endbMSLL = alfa*bMSLL- belta*bND;%%%%%%%%%%%%%%免疫种群与新生种群合并%%%%%%%%%%%%%%%%%%%f1=[af,bf];MSLL1=[aMSLL,bMSLL];[SortMSLL,Index]=sort(MSLL1);Sortf=f1(:,Index);gen=gen+1;trace(gen)=func2(Sortf(:,1));
end
%%%%%%%%%%%%%%%%%%%%%%%输出优化结果%%%%%%%%%%%%%%%%%%%%%%%%
Bestf=Sortf(:,1); %最优变量
trace(end); %最优值
figure,plot(trace)
xlabel('迭代次数')
ylabel('目标函数值')
title('亲和度进化曲线')%%%%%%%%%%%%%%%%%%%%%%%%%亲和度函数%%%%%%%%%%%%%%%%%%%%%%
function value=func2(x)
value=5*sin(x(1)*x(2))+x(1)*x(1)+x(2)*x(2);
endpython求解
import numpy as np
import pandas as pd
from tqdm import tqdm#进度条设置
import matplotlib.pyplot as plt
from pylab import *
import matplotlib; matplotlib.use('TkAgg')
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False####################初始化参数###################
D=2 #免疫个体维数
NP=50 #免疫个体数目
Xs=4 #取值上限
Xx=-4 #取值下限
G=200 #最大免疫代数
pm=0.7 #变异概率
alfa=2 #激励度系数
belta=1 #激励度系数
detas=0.2 #相似度阈值
gen=0 #免疫代数
Ncl=5 #克隆个数
deta0=0.5*Xs #邻域范围初值###目标函数
def calc_f(X):value = 5*np.sin(X[0]*X[1]) +(X[0] * X[0] + X[1] * X[1])return value##############计算个体浓度和激励度##########
def motivation(x,num):ND = np.zeros((num,1)) #临时数组nd = np.zeros((num,1)) #浓度for i in range(num):for j in range(num):tmp = np.sqrt(np.sum((x[i, :] - x[j, :]) ** 2))if (tmp > detas):ND[i,0] = 0else:ND[i,0] = 1nd[i,0] = np.sum(ND) / num## 激励度MSLL = np.zeros((num,1))for i in range(num):tmp = calc_f(x[i])MSLL[i,0] = tmpmtv = alfa * MSLL - belta * ndreturn mtv#################免疫算法####################种群初始化
f=np.random.random((NP,D))*(Xs-Xx)+Xx #shape(50, 2)MSLL=np.zeros((NP,1)) #存储当代种群激励度值#统一术语:亲和度值最高=激励度值最低
##计算初始种群亲和度值(激励度值)
for i in range(NP):MSLL[i]=calc_f(f[i])###激励度按升序排序
Index=np.argsort(MSLL,axis=0)
Index=Index[:,0]
Sortf=f[Index] #shape(50, 2)af=np.zeros((np.int(NP/2),D))#存储变异后的个体trace=[] #记录迭代激励度最优值
#########免疫循环############
for gen in tqdm(range(G)):#遍历每一次迭代for i in range(np.int(NP/2)):#遍历前一半样本#选激励度前NP/2个体进行免疫操作a = Sortf[i]#当前个体 .shape(2,)a=a.reshape(-1,2)Na = np.tile(a,(Ncl,1)) #对当前个体进行克隆 Na.shape=(5, 2)deta = deta0 / (gen+1) #刚开始迭代时,deta较大,随着迭代次数变多,deta减少for j in range(Ncl):#遍历每一个克隆样本for ii in range(D):#遍历每一个维度################变异####if np.random.random()<pm:#以一定概率进行变异Na[j,ii]=Na[j,ii]+(np.random.random()-0.5)*deta #元素=元素+加一个很小的随机数#边界条件处理if Na[j,ii]>Xs or Na[j,ii]<Xx:#如果在上下限范围外Na[j, ii]=np.random.uniform(Xx,Xs,1)#保留克隆源个体Na[0,:]=Sortf[i]#####克隆抑制,保留亲和度最高的个体NaMSLL = np.zeros((Ncl, 1)) # 存储变异种群激励度值for j in range(Ncl): # 遍历每一个克隆样本NaMSLL[j]=calc_f(Na[j])Index = np.argsort(NaMSLL, axis=0)#激励度按升序排序Index = Index[:, 0]NaSortf=Na[Index] #排序后的种群af[i]=NaSortf[0] #取最优#print(af.shape)#(25, 2)####免疫种群(克隆变异部分的)激励度aMSLL=motivation(af,af.shape[0])#print(aMSLL.shape)#(25, 1)###种群刷新,产生一半新生群体bf = np.random.random((np.int(NP/2),D))*(Xs-Xx)+Xx #bf.shape=(25, 2)bMSLL=motivation(bf,bf.shape[0])#新生种群的激励度 bMsLL.shape=(25, 1)#########免疫种群与新生种群合并#############f1 = np.concatenate((af,bf),axis=0) # 合并的种群 f1.shape=(50, 2)MSLL1=np.concatenate((aMSLL,bMSLL),axis=0) # 合并种群激励度值 MSLL1.shape=(50, 1)Index = np.argsort(MSLL1, axis=0)Index = Index[:, 0]Sortf = f1[Index] # shape(50, 2)trace.append(calc_f(f1[0]))#记录最优个体的激励度值############输出优化结果
Bestf=Sortf[0,:] #最优变量
print('最优变量',Bestf)
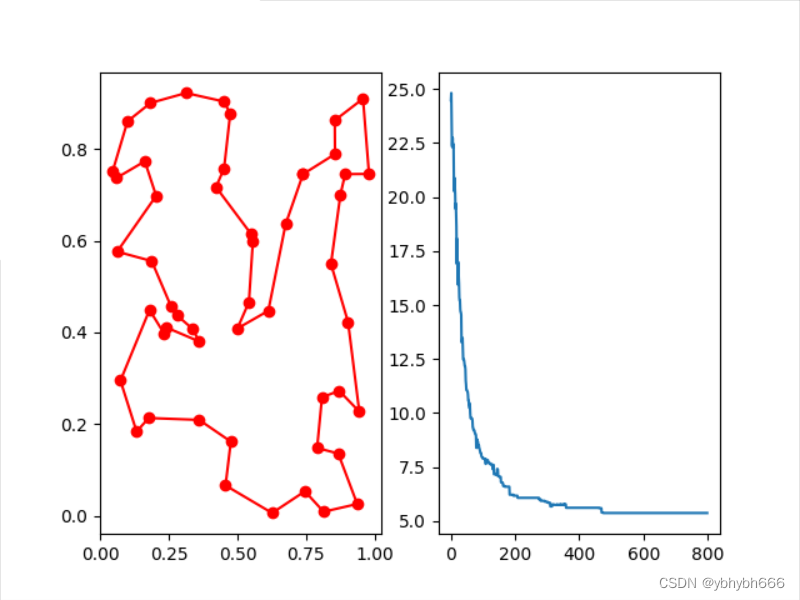
print('最优值',trace[-1] ) #最优值plt.plot(trace)
plt.title('迭代曲线')
plt.show()


免疫算法求解复杂约束问题
求解方法
- 一开始设计编码规则时,让解编码就只可能在可行区域内。典型的例子是算法做实数函数的优化,会给出 upper bound和lower bound,然后无论怎样的个体,解码后都在这两个bound之间 。
- 设计合理的变异算子,使得满足这些算子本身的特性的前提下,还让算子运算后的个体也在可行域内。此方法 例子见TSP求解。
- 罚函数法。万能方法。但罚函数太多或太严格,会导致效果很差。惩罚系数较大,族群会更加集中在可行域中,而不鼓励向不可行域探索。当惩罚系数过大,容易使算法收敛于局部最优;惩罚系数较小,族群会更积极在不可行域中进行大量探索,一定程度上能帮助寻找全局最优,但也有浪费算力的风险。当惩罚系数过小,算法可能会收敛于不可行解。
- 在变异/交叉之后加入一个判断语句,判断是否满足约束条件,如果不满足,有两个策略:超出边界的放到边界上。或者超出边界的,重新初始化。
注意事项
在优化算法中,每一步迭代都会更新个体和群体,虽然可以将有约束问题转换为无约束问题进行迭代求解,但是问题的解xi依然存在不满足约束条件的情况,因此需要编制一些规则来比较两个粒子的优劣,规则如下:
- 如果两个粒子xi和xj都可行,则比较其适应度函数f(xi)和f(xj),值小的粒子为优。
- 当两个粒子xi和xj都不可行,则比较惩罚项P(xi)和P(xj),违背约束程度小的粒子更优。
- 当粒子xi可行而粒子xj不可行,选可行解。
问题

流程图
此流程图是我自己的求解思路

python 版求解
import numpy as np
import pandas as pd
from tqdm import tqdm#进度条设置
import matplotlib.pyplot as plt
from pylab import *
import matplotlib; matplotlib.use('TkAgg')
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False####################初始化参数###################
D=2 #免疫个体维数
NP=50 #免疫个体数目
G=50 #最大免疫代数
pm=0.7 #变异概率
alfa=2 #激励度系数
belta=1 #激励度系数
detas=0.2 #相似度阈值
gen=0 #免疫代数
Ncl=5 #克隆个数
deta0=0.5*2 #邻域范围初值########################这里定义一些参数,分别是计算激励度函数和计算约束惩罚项函数############def calc_f(X):"""计算个体的目标函数值,X 的维度是 size * 2 """a = 10pi = np.pix = X[0]y = X[1]return 2 * a + x ** 2 - a * np.cos(2 * pi * x) + y ** 2 - a * np.cos(2 * 3.14 * y)def calc_e(X):"""计算个体的目惩罚项,X 的维度是 size * 2 """ee = 0"""计算第一个约束的惩罚项"""e1 = X[0] + X[1] - 6ee += max(0, e1)"""计算第二个约束的惩罚项"""e2 = 3 * X[0] - 2 * X[1] - 5ee += max(0, e2)return ee########################这里定义一些免疫算法相关的函数#############统一术语:激励度最低=亲和度最高#计算个体浓度和激励度##
def motivation(x,num):"""param x:群体param num:群体个数return : alfa*(目标函数值+惩罚项)-belta*浓度 .其中的目标函数值为最小化问题"""ND = np.zeros((num,1)) #临时数组nd = np.zeros((num,1)) #浓度for i in range(num):for j in range(num):tmp = np.sqrt(np.sum((x[i, :] - x[j, :]) ** 2))if (tmp > detas):ND[i,0] = 0else:ND[i,0] = 1nd[i,0] = np.sum(ND) / num #浓度## 激励度MSLL = np.zeros((num,1)) #MSLL存储 群体激励度。激励度=目标函数值+惩罚项for i in range(num):tmp = calc_f(x[i])#目标函数值ee=calc_e(x[i]) #惩罚项MSLL[i,0] = tmp+ee #激励度=目标函数值+惩罚项mtv = alfa * MSLL - belta * ndreturn mtv#alfa*(目标函数值+惩罚项)-belta*浓度#免疫操作函数:克隆、变异、变异抑制
def variation(Sortf):"""param Sortf:按亲和度大小排序后的群体return :af 经过克隆、变异、变异抑制后的群体"""af = np.zeros((np.int(NP / 2), D)) # 存储变异后的个体for i in range(np.int(NP / 2)): # 遍历前一半个体# 选激励度前NP/2个体进行免疫操作a = Sortf[i] # 当前个体 .shape(D,)a = a.reshape(-1, D) #(-1,维度D)Na = np.tile(a, (Ncl, 1)) # 对当前个体进行克隆 Na.shape=(Ncl, D)deta = deta0 / (gen + 1) # 刚开始迭代时,deta较大,随着迭代次数变多,deta减少for j in range(Ncl):#遍历每一个克隆样本for ii in range(D):#遍历每一个维度################变异####if np.random.random()<pm:#以一定概率进行变异Na[j,ii]=Na[j,ii]+(np.random.random()-0.5)*deta #元素=元素+加一个很小的随机数# x边界条件处理if Na[j, 0] > 2 or Na[j, 0] < 1: # 如果在上下限范围外Na[j, 0] = np.random.uniform(1, 2, 1)#y边界条件处理if Na[j, 1] > 0 or Na[j, 1] < -1: # 如果在上下限范围外Na[j, 1] = np.random.uniform(-1, 0, 1)# 保留克隆源个体Na[0, :] = Sortf[i]#####克隆抑制,保留亲和度最高(激励度最低)的个体NaMSLL = np.zeros((Ncl, 1)) # 存储变异种群激励度值for j in range(Ncl): # 遍历每一个克隆样本NaMSLL[j]=calc_f(Na[j])+calc_e(Na[j]) #目标函数值+惩罚项Index = np.argsort(NaMSLL, axis=0) # 激励度按升序排序Index = Index[:, 0]NaSortf = Na[Index] # 排序后的种群af[i] = NaSortf[0] # 取最优return af
#免疫操作:创建新生种群
def refresh():"""创建一般新生种群并返回"""bf = np.random.random((np.int(NP / 2), D))##边界条件处理for j in range(bf.shape[0]):#遍历每一个个体#x边界条件处理if bf[j, 0] > 2 or bf[j, 0] < 1: # 如果在上下限范围外bf[j, 0] = np.random.uniform(1, 2, 1)#y边界条件处理if bf[j, 1] > 0 or bf[j, 1] < -1: # 如果在上下限范围外bf[j, 1] = np.random.uniform(-1, 0, 1)return bf#############这里定义惩罚项带来的子代与父代的选择函数
#子代和父辈之间的选择操作
def update_best(parent,parent_fitness,parent_e,child,child_fitness,child_e):"""判:param parent: 父辈个体:param parent_fitness:父辈适应度值:param parent_e :父辈惩罚项:param child: 子代个体:param child_fitness 子代适应度值:param child_e :子代惩罚项:return: 父辈 和子代中较优者、适应度、惩罚项"""# 规则1,如果 parent 和 child 都没有违反约束,则取适应度小的if parent_e <= 0.0000001 and child_e <= 0.0000001:if parent_fitness <= child_fitness:return parent,parent_fitness,parent_eelse:return child,child_fitness,child_e# 规则2,如果child违反约束而parent没有违反约束,则取parentif parent_e < 0.0000001 and child_e >= 0.0000001:return parent,parent_fitness,parent_e# 规则3,如果parent违反约束而child没有违反约束,则取childif parent_e >= 0.0000001 and child_e < 0.0000001:return child,child_fitness,child_e# 规则4,如果两个都违反约束,则取适应度值小的if parent_fitness <= child_fitness:return parent,parent_fitness,parent_eelse:return child,child_fitness,child_e########################免疫算法流程开始数###############1.种群初始化
f=np.random.random((NP,D)) #shape(50, 2)
MSLL=np.zeros((NP,1)) #存储当代种群亲和值##2.计算初始种群激励度值(亲和度值)
for i in range(NP):MSLL[i]=calc_f(f[i])+calc_e(f[i])###3.激励度按升序排序
Index=np.argsort(MSLL,axis=0)
Index=Index[:,0]
Sortf=f[Index] #shape(50, 2) #排序后的初始群体###4.免疫循环
trace=[] #记录迭代激励度最优值
for gen in tqdm(range(G)):#遍历每一次迭代af=variation(Sortf)# 选择一半个体 进行克隆、变异、变异抑制aMSLL = motivation(af, af.shape[0]) #计算上一步得到的群体(亲和度) 激励度=alfa*(目标函数值+惩罚项)-belta*浓度 shape=(25,1)bf=refresh()#创建一半新生种群#bf.shape=(25, 2)bMSLL = motivation(bf, bf.shape[0]) # 新生种群的激励度 bMsLL.shape=(25, 1)# ##########种群刷新:免疫种群与新生种群合并##f1 = np.concatenate((af, bf), axis=0) # 合并的种群 f1.shape=(50, 2) f1为子代MSLL1 = np.concatenate((aMSLL, bMSLL), axis=0) # 合并种群激励度值 MSLL1.shape=(50, 1)# 更新群体#Sortf为父代群体parentfitness= motivation(Sortf, Sortf.shape[0]) #父代亲和度#子代和父代的选择,首先选对的for j in range(NP):#遍历每一个个体parent=Sortf[j]#父亲parent_fitness=parentfitness[j]#父亲亲和度parent_ee=calc_e(parent) #父亲惩罚项child=f1[j]#儿子child_fitness=MSLL1[j]#儿子亲和度child_ee=calc_e(child)#儿子惩罚项f1[j],child_fitness1,child_ee1=update_best(parent, parent_fitness, parent_ee,child, child_fitness,child_ee)#得到子代与父代选择更新后的群体f1MSLL2=motivation(f1, f1.shape[0])#种群激励度值 MSLL2.shape=(50, 1)Index = np.argsort(MSLL2, axis=0)Index = Index[:, 0]Sortf = f1[Index] # shape(50, 2)trace.append(calc_f(f1[0])) # 记录最优个体的激励度值############输出优化结果
Bestf=Sortf[0,:] #最优变量
print('最优变量',Bestf)
print('最优值',trace[-1] ) #最优值
print('惩罚项',calc_e(Bestf))plt.plot(trace)
plt.title('迭代曲线')
plt.show()

这题我以前用粒子群、遗传、差分 求过(见以前博客)。算法来的值为1.5.免疫算法算出来的为1。 可以看出在实数编码中,免疫算法比哪几种算法强。
离散编码免疫算法见:
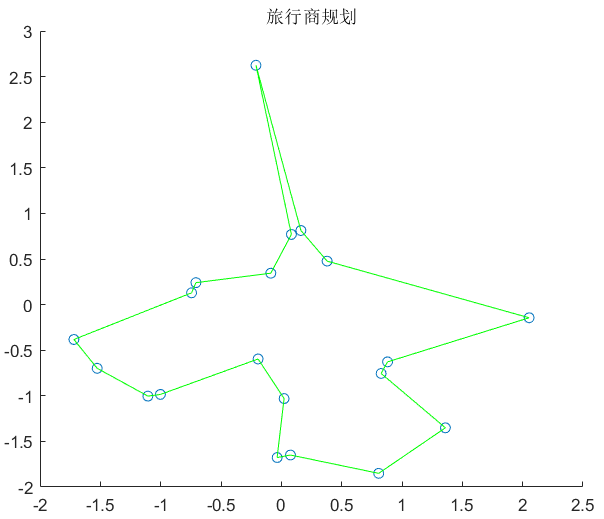
离散免疫算法求解旅行商问题(源码实现)
二进制编码免疫算法见:
免疫算法(二进制)算例(源码实现)

作者:电气-余登武