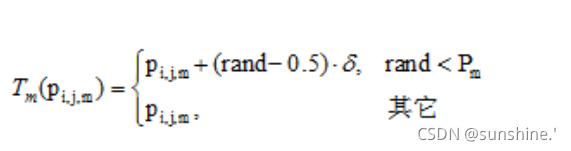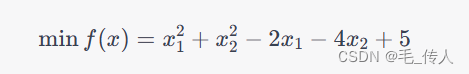人工免疫算法(Artificial Immune Algorithm,AIA)是一种基于生物免疫系统(BIS)的启发式优化算法,是对生物免疫算法的拓展和改进。AIA 借鉴了生物免疫系统中抗体和免疫记忆细胞等概念,采用人工免疫反应的方式进行全局优化。
与生物免疫算法不同的是,人工免疫算法采用了一些人工设计的策略,如变异、选择、克隆等策略,以提高算法的收敛速度和精度。因此,人工免疫算法具有很好的适应性和可扩展性,可以应用于多种优化问题。
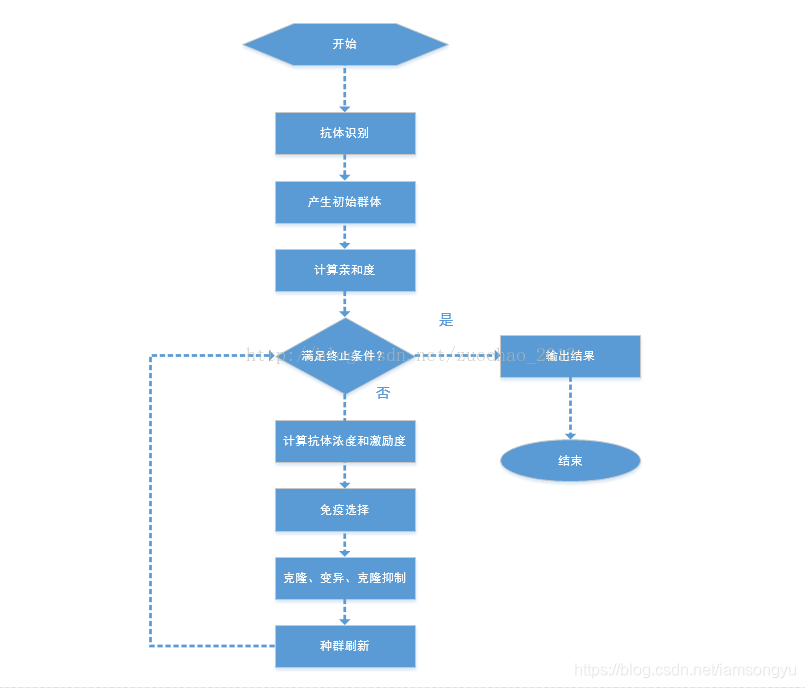
人工免疫算法的基本过程如下:
-
初始化种群:生成一组随机的抗体作为初始种群。
-
计算适应度:根据目标函数计算每个抗体的适应度。
-
免疫选择:根据抗体的适应度选择一部分抗体作为候选抗体。
-
克隆:对候选抗体进行克隆操作,生成一组克隆抗体。
-
变异:对克隆抗体进行变异操作,生成新的抗体。
-
免疫竞争:将新的抗体与原有抗体进行竞争,保留适应度更高的抗体。
-
记忆细胞更新:将适应度更高的抗体加入到记忆细胞中。
-
结束判断:如果满足停止条件,则输出最优解;否则,返回第 2 步。
人工免疫算法与生物免疫算法相比,具有以下优点:
-
算法更加灵活:人工免疫算法采用了一些人工设计的策略,如克隆、变异等策略,使算法更加灵活。
-
算法更加稳定:人工免疫算法可以避免生物免疫算法中的过拟合问题,从而使算法更加稳定。
-
算法更易于实现:人工免疫算法不需要考虑生物免疫系统中的复杂生理机制,因此更易于实现。
人工免疫算法已经在图像处理、数据挖掘、模式识别等领域得到了广泛的应用。
为了举例说明如何使用人工免疫算法求解函数的极值,我们以一个简单的一元函数为例:

在人工免疫算法中,抗体是一种可以识别和结合抗原的分子。在算法中,我们将优化问题中的可行解看作抗原,将算法中的搜索空间看作抗体空间。因此,我们需要将优化问题中的可行解映射到抗体空间中,以便用人工免疫算法来寻找最优解。
在一元函数的优化问题中,我们可以将可行解看作实数x
,即函数 f(x)的自变量。因此,我们可以将实数 x映射到抗体空间中,将其视为一种抗体,用人工免疫算法来优化函数f(x)
。
当然,在实际问题中,我们也可以将可行解看作多维向量或矩阵等形式,用人工免疫算法来进行优化。不过,无论是一元函数还是多维优化问题,我们都需要将可行解映射到抗体空间中,以便进行人工免疫算法的优化过程。