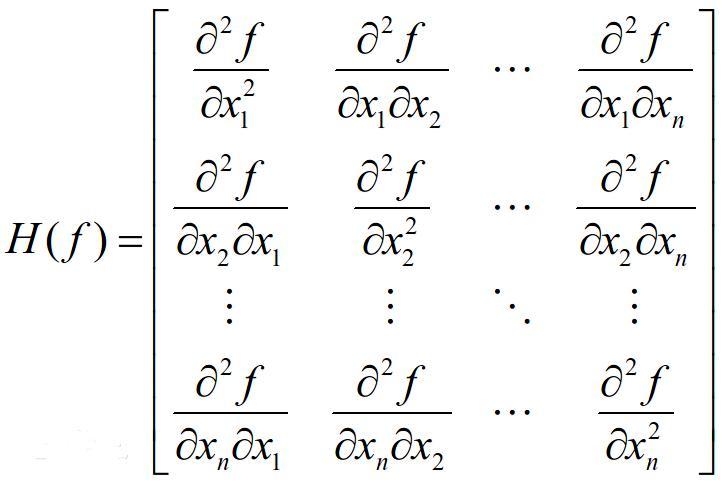上面的表达式成立的条件是 当且仅当  Δx 无线趋近于0。此时上式等价与：

求解：

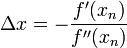
得出迭代公式：

一般认为牛顿法可以利用到曲线本身的信息，比梯度下降法更容易收敛（迭代更少次数），如下图是一个最小化一个目标方程的例子，红色曲线是利用牛顿法迭代求解，绿色曲线是利用梯度下降法求解。

在上面讨论的是2维情况，高维情况的牛顿迭代公式是：

其中H是hessian矩阵，定义为如上文描述。

高维情况依然可以用牛顿迭代求解，但是问题是Hessian矩阵引入的复杂性，使得牛顿迭代求解的难度大大增加，但是已经有了解决这个问题的办法就是Quasi-Newton methond，不再直接计算hessian矩阵，而是每一步的时候使用梯度向量更新hessian矩阵的近似。

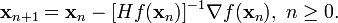
拟牛顿法

拟牛顿法(Quasi-Newton Methods)是求解非线性优化问题最有效的方法之一，于20世纪50年代由美国Argonne国家实验室的物理学家W. C. Davidon所提出来。Davidon设计的这种算法在当时看来是非线性优化领域最具创造性的发明之一。不久R. Fletcher和M. J. D. Powell证实了这种新的算法远比其他方法快速和可靠，使得非线性优化这门学科在一夜之间突飞猛进。在之后的20年里，拟牛顿方法得到了蓬勃发展，出现了大量的变形公式以及数以百计的相关论文。

拟牛顿法和最速下降法(Steepest Descent Methods)一样只要求每一步迭代时知道目标函数的梯度。通过测量梯度的变化，构造一个目标函数的模型使之足以产生超线性收敛性。这类方法大大优于最速下降法，尤其对于困难的问题。另外，因为拟牛顿法不需要二阶导数的信息，所以有时比牛顿法(Newton's Method)更为有效。如今，优化软件中包含了大量的拟牛顿算法用来解决无约束，约束，和大规模的优化问题。

Hessian Matrix（黑塞矩阵、海森矩阵、海瑟矩阵、海塞矩阵 etc.）,它是一个多元函数的二阶偏导数构成的方阵，用以描述函数的局部曲率。黑塞矩阵最早于19世纪由德国数学家Ludwig Otto Hesse提出，并以其名字命名。黑塞矩阵常用于牛顿法解决优化问题。

对于一个实值多元函数  ，如果函数的二阶偏导数都存在，则定义的黑塞矩阵为：

其中表示对第 i 个变量的微分算子，。那么，f 的黑塞矩阵即:

性质：

1. 对称性：

如果函数 f 在D区域内二阶连续可导，那么 f 黑塞函数H(f)在D内为对称方阵。

2. 多元函数极值的判定：

如果实值多元函数 f(x1,x2,...)二阶连续可导，并且在临界点M(xi)（i=1,2,...,n, 且xi已知）处梯度（一阶导数）等于零，即，，M为驻点。仅仅通过一阶导数无法判断在临界点M处是极大值还是极小值。

记

• 如果H(M)是正定矩阵，则临界点M处是一个局部的极小值。
• 如果H(M)是负定矩阵，则临界点M处是一个局部的极大值。
• 如果H(M)是不定矩阵，则临界点M处不是极值。

提到hessian矩阵奇异，就需要首先介绍一下牛顿法，拟牛顿法，最速下降法。

牛顿法

1、求解方程。

并不是所有的方程都有求根公式，或者求根公式很复杂，导致求解困难。利用牛顿法，可以迭代求解。

原理是利用泰勒公式，在x0处展开，且展开到一阶，即f(x) = f(x0)+(x－x0)f'(x0)

求解方程f(x)=0，即f(x0)+(x-x0)*f'(x0)=0，求解x = x1=x0－f(x0)/f'(x0)，因为这是利用泰勒公式的一阶展开，f(x) = f(x0)+(x－x0)f'(x0)处并不是完全相等，而是近似相等，这里求得的x1并不能让f（x）=0，只能说f(x1)的值比f(x0)更接近f（x）=0，于是乎，迭代求解的想法就很自然了，可以进而推出x(n+1)=x(n)－f(x(n))/f'(x(n))，通过迭代，这个式子必然在f（x*）=0的时候收敛。整个过程如下图：

在最优化的问题中，线性最优化至少可以使用单纯行法求解，但对于非线性优化问题，牛顿法提供了一种求解的办法。假设任务是优化一个目标函数f，求函数f的极大极小问题，可以转化为求解函数f的导数f'=0的问题，这样求可以把优化问题看成方程求解问题（f'=0）。剩下的问题就和第一部分提到的牛顿法求解很相似了。

这次为了求解f'=0的根，把f（x）的泰勒展开，展开到2阶形式：

上面的表达式成立的条件是 当且仅当  Δx 无线趋近于0。此时上式等价与：

求解：

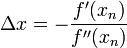
得出迭代公式：

一般认为牛顿法可以利用到曲线本身的信息，比梯度下降法更容易收敛（迭代更少次数），如下图是一个最小化一个目标方程的例子，红色曲线是利用牛顿法迭代求解，绿色曲线是利用梯度下降法求解。

在上面讨论的是2维情况，高维情况的牛顿迭代公式是：

其中H是hessian矩阵，定义为如上文描述。

高维情况依然可以用牛顿迭代求解，但是问题是Hessian矩阵引入的复杂性，使得牛顿迭代求解的难度大大增加，但是已经有了解决这个问题的办法就是Quasi-Newton methond，不再直接计算hessian矩阵，而是每一步的时候使用梯度向量更新hessian矩阵的近似。

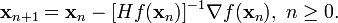
拟牛顿法

拟牛顿法(Quasi-Newton Methods)是求解非线性优化问题最有效的方法之一，于20世纪50年代由美国Argonne国家实验室的物理学家W. C. Davidon所提出来。Davidon设计的这种算法在当时看来是非线性优化领域最具创造性的发明之一。不久R. Fletcher和M. J. D. Powell证实了这种新的算法远比其他方法快速和可靠，使得非线性优化这门学科在一夜之间突飞猛进。在之后的20年里，拟牛顿方法得到了蓬勃发展，出现了大量的变形公式以及数以百计的相关论文。

拟牛顿法和最速下降法(Steepest Descent Methods)一样只要求每一步迭代时知道目标函数的梯度。通过测量梯度的变化，构造一个目标函数的模型使之足以产生超线性收敛性。这类方法大大优于最速下降法，尤其对于困难的问题。另外，因为拟牛顿法不需要二阶导数的信息，所以有时比牛顿法(Newton's Method)更为有效。如今，优化软件中包含了大量的拟牛顿算法用来解决无约束，约束，和大规模的优化问题。

在讲解拟牛顿法之前，先介绍几个概念：

无约束优化问题：

线搜索方法：

这里的dk代表搜索方向，ak代表搜索步长。（精确搜索：f(x+ad)达到最小；Wolfe搜索）

精确搜索：

Wolfe非精确搜索：

搜索方向：

最速下降法：

共轭梯度法：

牛顿法：

牛顿法是下列问题的解：

拟牛顿法：，对称，正定。

牛顿法的条件：

       拟牛顿法的条件： ， ，

拟牛顿法的基本思想如下。首先构造目标函数在当前迭代

的二次模型：

这里

是一个对称正定矩阵，于是我们取这个二次模型的 最优解 作为搜索方向，并且得到新的迭代点

，其中我们要求步长

满足Wolfe条件。这样的迭代与牛顿法类似，区别就在于用近似的Hesse矩阵

代替真实的Hesse矩阵。所以拟牛顿法最关键的地方就是每一步迭代中矩阵

的更新。现在假设得到一个新的迭代

，并得到一个新的二次模型：

                                                                                              

我们尽可能地利用上一步的信息来选取 。具体地，我们要求

，从而得到割线方程：

拟牛顿法的基本思想如下。首先构造目标函数在当前迭代

我们尽可能地利用上一步的信息来选取 。具体地，我们要求

，从而得到割线方程：

常见的几种方法用来求解B，DFP方法，BFGS方法，SR1方法，Broyden族方法。

DFP方法编辑

记

，

，

，DFP公式为

该公式最初由Davidon于1959年提出，随后被Fletcher和Powell研究和推广。DFP方法是秩-2更新的一种，由它产生的矩阵

是正定的，而且满足这样的极小性：

3BFGS方法编辑

DFP更新 公式非常有效，但很快就被BFGS公式取代。BFGS与DFP十分类似，是另一种秩-2更新，以其发明者Broyden, Fletcher, Goldfarb和Shanno的姓氏首字母命名。BFGS 公式为

由他产生的矩阵

同样保持正定性，而且也满足一个极小性：

BFGS和DFP 公式在形式上是对称的：

与

对称，

与

对称。但是BFGS比DFP更加有效。

4SR1方法编辑

5Broyden族编辑