摘自矩阵（数学术语）_百度百科
定义
由 m × n 个数aij排成的m行n列的数表称为m行n列的矩阵，简称m × n矩阵。记作：
这m×n 个数称为矩阵A的元素，简称为元，数aij位于矩阵A的第i行第j列，称为矩阵A的(i,j)元，以数 aij为(i,j)元的矩阵可记为(aij)或(aij)m × n，m×n矩阵A也记作Amn。
元素是实数的矩阵称为实矩阵，元素是复数的矩阵称为复矩阵。而行数与列数都等于n的矩阵称为n阶矩阵或n阶方阵
。
基本运算
矩阵运算在科学计算中非常重要 [8]
，而矩阵的基本运算包括矩阵的加法，减法，数乘，转置，共轭和共轭转置 [1]
[9]
。
加法
矩阵的加法满足下列运算律(A，B，C都是同型矩阵)：
减法
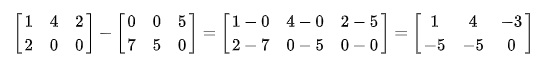
数乘
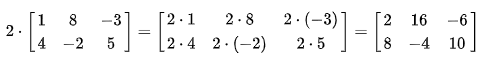
矩阵的数乘满足以下运算律：
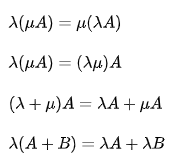
矩阵的加减法和矩阵的数乘合称矩阵的线性运算 。
转置
把矩阵A的行和列互相交换所产生的矩阵称为A的转置矩阵（
),这一过程称为矩阵的转置
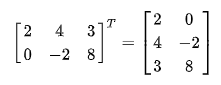
矩阵的转置满足以下运算律：
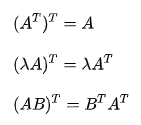
共轭
矩阵的共轭定义为:
一个2×2复数矩阵的共轭（实部不变，虚部取负）如下所示 ：
则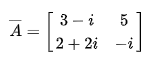
共轭转置
矩阵的共轭转置定义为：
,也可以写为：
,或者写为
。一个2×2复数矩阵的共轭转置如下所示：
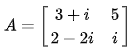则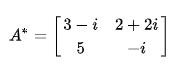 
乘法
主条目：矩阵乘法
两个矩阵的乘法仅当第一个矩阵A的列数和另一个矩阵B的行数相等时才能定义。如A是m×n矩阵和B是n×p矩阵，它们的乘积C是一个m×p矩阵
，它的一个元素：
并将此乘积记为:
。
例如：
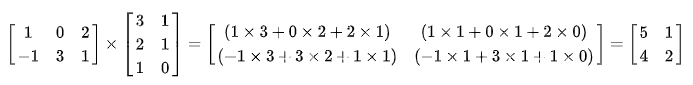
矩阵的乘法满足以下运算律：
结合律：(AB)C=A(BC)
左分配律：(A+B)C = AC+BC
右分配律：C(A+B)=CA+CB
矩阵乘法不满足交换律。
行列式
主条目：行列式
一个n×n的正方矩阵A的行列式记为
或者
,一个2×2矩阵的行列式可表示如下
：
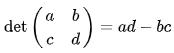
一个n×n矩阵的行列式等于其任意行（或列）的元素与对应的代数余子式乘积之和，即：
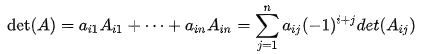
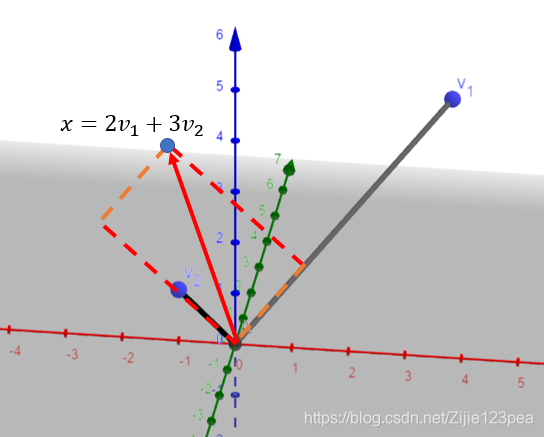
特征值与特征向量
主条目：特征值，特征向量
n×n的方块矩阵A的一个特征值和对应特征向量是满足
的标量以及非零向量 。其中v为特征向量，
为特征值。
A的所有特征值的全体，叫做A的谱 [13]
，记为
。矩阵的特征值和特征向量可以揭示线性变换的深层特性 。
矩阵的迹
主条目：矩阵的迹
n×n矩阵A的对角元素之和称为矩阵A的迹(trace),记作tr(A) , 即
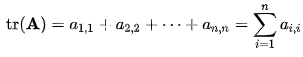
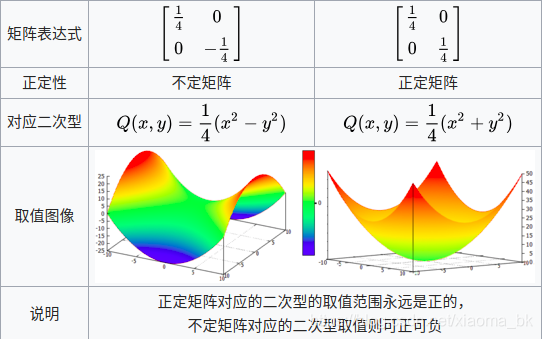
正定性
n×n的实对称矩阵A如果满足对所有非零向量
，对应的二次型
若Q>0，就称A为正定矩阵。若Q<0则A是一个负定矩阵，若Q≥0，则A为半正定矩阵，若A既非半正定，也非半负定，则A为不定矩阵
。对称矩阵的正定性与其特征值密切相关。矩阵是正定的当且仅当其特征值都是正数 。
矩阵的分解
主条目：矩阵分解
矩阵分解是将一个矩阵分解为比较简单的或具有某种特性的若干矩阵的和或乘积 [13]
，矩阵的分解法一般有三角分解、谱分解、奇异值分解、满秩分解等。
三角分解
设
,则A可以唯一地分解为
,其中U1是酉矩阵，R是正线上三角复矩阵，或A可以唯一地分解为其中L是正线上三角复矩阵，是酉矩阵
。
谱分解
谱分解（Spectral decomposition）是将矩阵分解为由其特征值和特征向量表示的矩阵之积的方法。需要注意只有对可对角化矩阵才可以施以特征分解
。
奇异值分解
假设M是一个m×n阶矩阵，其中的元素全部属于域K，也就是实数域或复数域。如此则存在一个分解使得
其中U是m×m阶酉矩阵；Σ是m×n阶实数对角矩阵；而V*，即V的共轭转置，是n×n阶酉矩阵。这样的分解就称作M的奇异值分解 [17]
。Σ对角线上的元素Σi,i即为M的奇异值。常见的做法是将奇异值由大而小排列。如此Σ便能由M唯一确定了。
满秩分解
设
，若存在矩阵
及
，使得A=FG，则称其为的A一个满秩分解
。
LUP分解
LUP分解的思想就是找出三个n×n矩阵L,U,P，满足PA=LU其中L是一个单位下三角矩阵，U是一个单位上三角矩阵，P是一个置换矩阵。 而满足分解条件的矩阵L,U,P称为矩阵A的一个LUP分解
。
