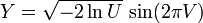正态分布
我们来对某一个年级做一项调查,看一看这个年级到底有多巨。于是,他们统计了每个同学一周刷题的时间。得到的结果如下:
可以看出,大多数人每周都有7-8个小时做题,有少部分蒟蒻(比如我)每周只有1-3个小时做题,而一些神犇(比如这位)每周有13-15个小时刷题。
整个图表大致上是轴对称的。中间最多,两边最少。这种分布图称为正态分布。
正态分布又称为高斯分布,他是由高斯发现的。正态分布也是最常见的概率分布。对于上面那个例子,我们统计足够多的人、将时间区间分的足够小之后,就可以画出他的概率密度曲线:
概率密度曲线一定满足 ∫ − ∞ + ∞ f ( x ) = 1 \int_{-\infty}^{+\infty}f(x)=1 ∫−∞+∞f(x)=1正态分布也不例外。
其实上面的例子并不是真正的正态分布,因为不存在负时间。但是,真正的正态分布的概率密度曲线可以向负无穷和正无穷无限延伸。图像以 x x x轴为渐近线,也就是:
lim x → ∞ f ( x ) = 0 \lim\limits_{x\rightarrow\infty}f(x)=0 x→∞limf(x)=0
我们的高斯给出了正态分布的数学表达式:
f ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 f(x)=\dfrac1{\sqrt{2\pi}\sigma}e^{-\dfrac{(x-\mu)^2}{2\sigma^2}} f(x)=2πσ1e−2σ2(x−μ)2
通常我们用 N ( μ , σ 2 ) N(\mu,\sigma^2) N(μ,σ2)来表示正态分布。
其中 μ \mu μ是数学期望,就是图像上的对称轴。在之前的例子中就是平均每个人每周能有多长时间做题。换句话说,图像关于 μ \mu μ对称, f ( μ + c ) = f ( μ − c ) f(\mu+c)=f(\mu-c) f(μ+c)=f(μ−c)
σ \sigma σ是标准差,也就是图像上的"峰"陡峭程度。标准差越大,数据越分散,标准差越小,数据越集中。
正态分布满足期望、中位数和众数相同,都是对称轴。图像的最高点 f ( μ ) = 1 2 π σ f(\mu)=\dfrac1{\sqrt{2\pi}\sigma} f(μ)=2πσ1
回忆一下初中地理的内容。年降水量其实就是服从了正态分布。
(随便找了个图贴上)
人的身高也近似是正态分布。
可以说,大多数概率分布都是正态分布。甚至连宇宙信号噪声这样看似随机的变量,如果你对每个时刻的每个值进行统计,它也是正态分布的。这样的噪声也沾上了高斯分布的荣光,故名高斯噪声。
在正态分布中,有这样一种特殊的正态分布。它不高不矮,不胖不瘦,不偏不倚。它,叫做,标准正态分布。
标准正态分布之所以标准,并不是因为大多数正态分布都是标准正态分布,而是他的概率密度函数图像就很标准。
标准正态分布的概率密度函数是 φ ( x ) = 1 2 π e − x 2 2 \varphi(x)=\dfrac1{\sqrt{2\pi}}e^{-\dfrac{x^2}2} φ(x)=2π1e−2x2
也就是 N ( 0 , 1 ) N(0,1) N(0,1)。
标准正态分布图像关于 x = 0 x=0 x=0对称。任何正态分布 N ( μ , σ 2 ) N(\mu,\sigma^2) N(μ,σ2)都可以通过线性变换变成标准正态分布。变换方法如下:
若 x ∼ N ( μ , σ 2 ) x\sim N(\mu,\sigma^2) x∼N(μ,σ2),则 y = x − μ σ ∼ N ( 0 , 1 ) y=\dfrac{x-\mu}\sigma \sim N(0,1) y=σx−μ∼N(0,1)
我们用 φ \varphi φ表示标准正态分布的概率密度曲线, Φ \Phi Φ表示概率分布曲线。
根据概率分布曲线的定义,若 x ∼ N ( 0 , 1 ) x\sim N(0,1) x∼N(0,1),则
P ( a < x < b ) = Φ ( b ) − Φ ( a ) P(a<x<b)=\Phi(b)-\Phi(a) P(a<x<b)=Φ(b)−Φ(a)
所以,若 x ∼ N ( μ , σ 2 ) x\sim N(\mu,\sigma^2) x∼N(μ,σ2)
P ( a < x < b ) = Φ ( b − μ σ ) − Φ ( a − μ σ ) P(a<x<b)=\Phi(\dfrac{b-\mu}\sigma)-\Phi(\dfrac{a-\mu}\sigma) P(a<x<b)=Φ(σb−μ)−Φ(σa−μ)
在最后,我说一下" 3 σ 3\sigma 3σ标准"
我们通过查表可以知道:
P ( ∣ x − μ ∣ < σ ) ≈ 0.6826 P(|x-\mu|<\sigma)\approx0.6826 P(∣x−μ∣<σ)≈0.6826
P ( ∣ x − μ ∣ < 2 σ ) ≈ 0.9544 P(|x-\mu|<2\sigma)\approx0.9544 P(∣x−μ∣<2σ)≈0.9544
P ( ∣ x − μ ∣ < 3 σ ) ≈ 0.9974 P(|x-\mu|<3\sigma)\approx0.9974 P(∣x−μ∣<3σ)≈0.9974
所以, x x x的取值几乎全集中在 ( μ − 3 σ , μ + 3 σ ) (\mu-3\sigma,\mu+3\sigma) (μ−3σ,μ+3σ)区间中,在这个区间外面的概率不到 0.3 % 0.3\% 0.3%





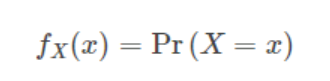






![[R语言]正态分布](https://img-blog.csdnimg.cn/img_convert/0763ef1d012bcf456bd17fea7af87ad0.png)