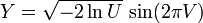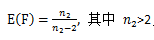概率分布、总体分布、抽样分布,一开始很容易搞混,还以为是同一个理论,不同的概念,毕竟都是分布,又都是统计学里面的概率。今天就来理解理解这个东西吧。
概率分布是指随机变量的各取值与该取值对应的概率之间呈现的规律。这里,随机变量具体指什么是根据我们提供的数据的变化而变化的。当我们需要得到数据总体的取值分布时,随机变量表征的就是数据总体,此时,概率分布就是总体分布。在抽样时,我们对数据总体做n次抽样,每次抽m个数据作为样本,每次抽样后,计算样本的均值或者方差等,n次抽样得到的n各均值的函数表征就是当下的随机变量,根据这个随机变量得到的概率分布就是抽样分布。因此,概率分布是一个更为广泛的概念,而总体分布、抽样分布是概率分布的特殊应用。
概率分布挺神奇的,也很复杂。各种不同的分布,中心极限定理,各种分布之间的转换,...,感觉都是大学问。今天呢,先罗列目前收集到的常见的分布。后续再一个个啃。
1.伯努利分布
伯努利分布也就是二项式分布,个人总结为“抛硬币”分布。
在伯努利试验中,只有两个事件:A和B,我们可以把抛硬币抛出“花”定为A,它的概率为p;抛出“币值”定为B,它的概率为q,事件A和B是互斥的,且p+q=1。随机变量X表示在n次试验中,事件A发生了x次,这样一来,X的取值范围为[0,n]之间的整数。该分布的函数
伯努利分布概率函数
2.正态分布
“钟形”曲线,是概率分布中特别重要的分布,也是应用最广泛的概率分布,由高斯最先在天文学研究中应用,后来成为中心极限定理中其他分布的渐进目标。它的重要统计量,均值u和标准差sigma。它的概率密度函数为
正态分布概率密度函数
分布的累积概率函数为
正态分布概率累积函数
当期望为0,标准差为1时,就是标准正态分布了。
3.泊松分布、指数分布和韦伯分布
3.1. 泊松分布
泊松分布是与世间和速度相关的分布,其随机变量X表示的在一段时间内,事件发生的次数,例如,每个月,某个航班晚点的次数。泊松分布中的随机变量不是毫无证据乱估计的,它带了一个先验参数lambda,这个参数表示以往的先验数据中该事件在单位时间内的平均发生率,如,根据前2年的数据统计出,某航班每月平均晚点次数为8次,lambda=8,那么我们可以通过泊松分布计算当月晚点x次的概率。
泊松分布的概率函数:
泊松分布概率函数
3.2 指数分布
和泊松分布一样与世间相关的分布还有指数分布和韦伯分布。泊松分布所使用的速率参数lambda是直接为事件频数,而指数分布更多表征那些不常发生的事件,如故障,交通事故,发生频数很低,用指数分布就更合适。指数分布如下
指数分布概率函数
3.3 韦伯分布
泊松分布和指数分布都不考虑时间在周期内发生变化,这种用于处理事件比较固定或者改变更长很长的事件是没有问题的。但是,有些事件会随着时间变化而改变,韦伯分布引入形状参数beta允许事件发生率变化和比例参数eta表示事件的生命周期特征。概率函数为
weibull分布概率函数
4.多项分布
伯努利分布是二项分布,事件只有两个,但是,实际上很多问题都不会只有两个事件。类比于伯努利分布,最简单的例子如掷骰子,可能掷出的点数有1,2,3,4,5,6,就有6个事件。我们可以设定1-6个随机变量,每个随机变量表示n次投掷后,某个点数被投掷出来的次数。例如,1点被投中的次数为X1, 2点被投中的次数为X2,3点被投中的次数为X3,......6个随机变量的概率和为1。这6个随机变量的概率分布就是一个多项分布。
多项分布的概率函数为
在投掷单个骰子中,k=6。
5.均匀分布
均匀分布是一定范围内,随机变量各取值的概率相等。个人理解,就是一个袋子里面有n颗球,每个球的大小、材料、制作工艺都是完全一样的,不同的是印了不同编号,这些球被随机打乱。然后有个人伸一只手进去摸一个,摸中每个球的机会可以看做是均等的,这n颗球的编号就是随机变量,随机变量的概率是均等的,也就是均匀分布。
均分分布的概率密度函数
均匀分布的概率函数
6.柯西分布
这个分布完全没研究过,暂时也不知道到底可以干啥,或者是从哪里来的,先列在这儿,后续再啃。
柯西分布概率密度函数
其中,a是超参数,当a为1的时候是个特例,估计就和标准正态分布一样吧。
7.贝塔分布及其涉及到的函数以及相关分布
7.1 伽玛函数和贝塔函数
贝塔分布涉及到两个函数——伽马函数和贝塔函数,其中伽玛函数是接下来的好几个分布都会用到的。
伽玛函数是欧拉在解决哥德巴赫提出的一个问题时导出来的,它长这样子
伽玛函数
这个积分并不复杂,从公式上很容易看出它所具有的特性
经过证明(证明过程暂时没搞懂)可以等到
这个公式是贝塔函数用伽玛函数表示的重要基石。首先,贝塔函数
贝塔函数
贝塔函数可以由伽玛函数很优雅的表示出来。
7.2 伽玛分布
伽玛分布是一种连续分布,他包含两个参数,alpha和beta,其随机变量x表示等到第alpha件事发生需要等到多长时间。和泊松分布系列是不是有点异曲同工?其中,alpha是形状参数,感觉和韦伯分布中的形状参数有点关联,beta是尺度参数,和韦伯参数中的eta比例参数关联。
伽玛分布概率密度函数
样子长得和泊松分布有点像,但是泊松分布随机变量的取值是正整数,而伽玛分布的取值是正实数,一个离散一个连续。
到这里,想提一下分布间不算特点的特点,二项分布、泊松系列分布、以及这里的伽玛分布和贝塔分布的随机变量都只有一个,也就是一维的;而多项分布以及后面会提到的狄利克雷分布,随机变量都是多个的,是多维的;正态分布、均匀分布可以是一维,也可以是多维的。
7.3 贝塔分布
贝塔分布可看做是某个事件发生的概率的概率分布,它的随机变量x是事件发生的概率,因此必须满足所有概率变量都必须满足的条件
并且贝塔分布和二项分布是共轭的。这里共轭是什么样的呢?就是根据先验beta分布经过二项分布数据加入后,得到的后验分布依然是beta分布。回顾抛硬币事件和伯努利分布,我们把伯努利分布的随机变量定为n次投掷中投出“花”的次数x’,也就是说伯努利是次数的概率。同样,我们用抛硬币事件来解释贝塔分布。beta分布的随机变量就是n次中投出“花”的次数为x’的各种概率x,其概率密度为
7.4 狄利克雷分布
贝塔分布和伯努利分布共轭,狄利克雷分布和多项分布共轭。狄利克雷是贝塔的多维度随机变量延伸。
其中,B是多维贝塔函数,表示为
这一块挺重要的,后续需要深入理解。
8.卡方分布、学生t分布和F分布
8.1 卡方分布
这三个分布在统计学中很常见也挺重要的。在早期文本特征抽取中,卡方检验经常被使用。卡方分布的随机变量是一系列服从标准正态分布的随机变量的平方和,即
累积概率函数为
卡方分布的累积概率函数
其中,v是随机变量的自由度。哈哈,伽玛函数又出现了。
8.2 学生t分布
t分布有个有趣的又来,最初是由吉尼斯啤酒公司的员工发现的,和啤酒居然能产生联系。t分布也是钟形曲线。只是正态分布是由数据总体的均值和标准差决定的,而在早年没有计算机的时代,数据量稍微大一点,计算就很费劲,总体的标准差计算起来就更费劲。因此,抽样后,用样本标准差作为总体标准差的估计量,所以,t分布也是钟形曲线。
t分布的概率密度函数
其中t是分布的随机变量,这个随机变量可以由标准正态分布的随机变量经过t变换得来。当然,实际应用中应该是由t变换成标准正态分布中的随机变量吧。变换过程
其中卡方是标准正态分布中自由度为v的随机变量的卡方值。
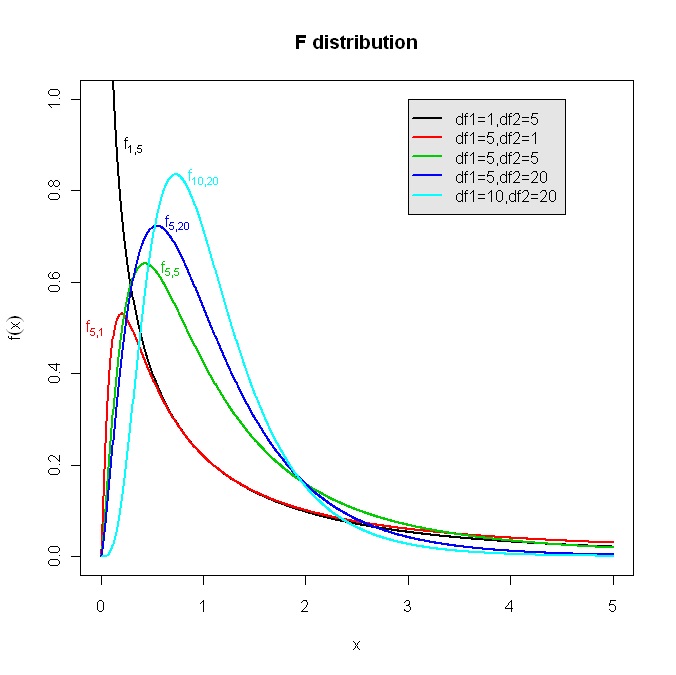
8.3 F分布
两个随机变量X, Y,X服从自由度为m的卡方分布,Y服从自由度为n的卡方分布,且这两个卡方分布彼此独立,那么变量
服从F分布。F分布的概率密度函数
总的来说,这三个分布都跟标准正态分布密切相关,同时有都跟卡方计算相关。
总的来说,这些个分布尽管从不同的试验中来,或者表征不同的统计问题,但他们之间总能彼此关联上,例如,伯努利分布通过中心极限定理可以逼近正态分布;泊松分布系列又和贝塔系列分布扯得上关系,同时,泊松系列分布也可逼近正态分布;卡方系列分布与标准正态分布密切相关,以及伽玛函数出现在很多分布中。种种关系很复杂,却也很有趣,后续继续加油吧。