F分布是1924年英国统计学家R.A.Fisher提出,并以其姓氏的第一个字母命名的。它是一种非对称分布,有两个自由度,且位置不可互换。设X服从自由度为n1的卡方分布, Y服从自由度为n2的卡方分布,且X,Y独立,则称随机变量F=(X⁄n1 )/(Y⁄n2 )服从自由度为(n1,n2)的F分布,记为F~F(n1,n2)。其中n1称为第一自由度,n2称为第二自由度。
由F分布的公式可知,1/F~ F(n2,n1)。
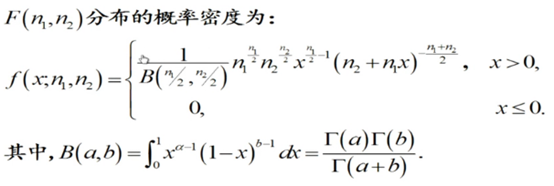
F(n1,n2)的概率密度函数的图形为:(对于不同的自由度,图形也有差别,此处仅举2个例子)。

一、F分布的特征:
F分布有两个参数,对应的是两个自由度。F分布的均值和方差应该怎样来看呢?
1、均值:
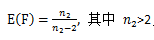
2、方差:
F分布及其应用
article/2025/8/30 2:54:16
相关文章
TeamTalk各个服务的IP配置方案
本人微信公众号:CPP进阶之旅 如果觉得这篇文章对您有帮助,欢迎关注 “CPP进阶之旅” 学习更多技术干货 TeamTalk各个服务的IP配置方案 1.纯公司内网2.公网ip3.公网ip,路由器映射相关文章重要说明 TeamTalk源码中的IM_SERVER下共有8种服务器&a…
TeamTalk部署详细教程(最全最新TeamTalk部署教程助你一次部署成功)
本人微信公众号:CPP进阶之旅 如果觉得这篇文章对您有帮助,欢迎关注 “CPP进阶之旅” 学习更多技术干货 TeamTalk部署详细教程 背景1、更新操作系统2、删除已经安装的软件3、安装必要的依赖软件4、安装mysql4.1 下载4.2 解压编译4.3 添加mysql用户4.4 修改…
新版TeamTalk部署教程
原文转自蓝狐(bluefox)的博客:https://blog.csdn.net/simongyley/article/details/45535429。对文中部分问题做了修改。 0、简介 新版TeamTalk已经在2015年03月28日发布了,目前版本定为1.0.0版本,后续版本号会按照如下…
(TeamTalk服务端源码分析一)TeamTalk服务端部署
TeamTalk服务端部署 在分析TeamTalk的各个服务器代码之前,我们先搭建一套服务端环境,结合之前的客户端,看一下一个IM聊天工具的基本功能。
一、部署环境 系统:centos7 X64位
二,部署步骤 1, 安装git gcc …
windows 10 Docker Desktop TeamTalk 安装笔记
目录
1、运行docker centos:7 版本系统 1.1进入 docker系统
1.2更新系统
1.3安装依赖软件
2、安装MySQL
2.1下载解压mysql
2.2解压mysql
2.3 编译安装mysql
2.3创建mysql用户
2.4创建my.cnf配置 2.5初始化
2.6其他配置
2.7启动mysql
2.8修改密码
2.9完成mysq…
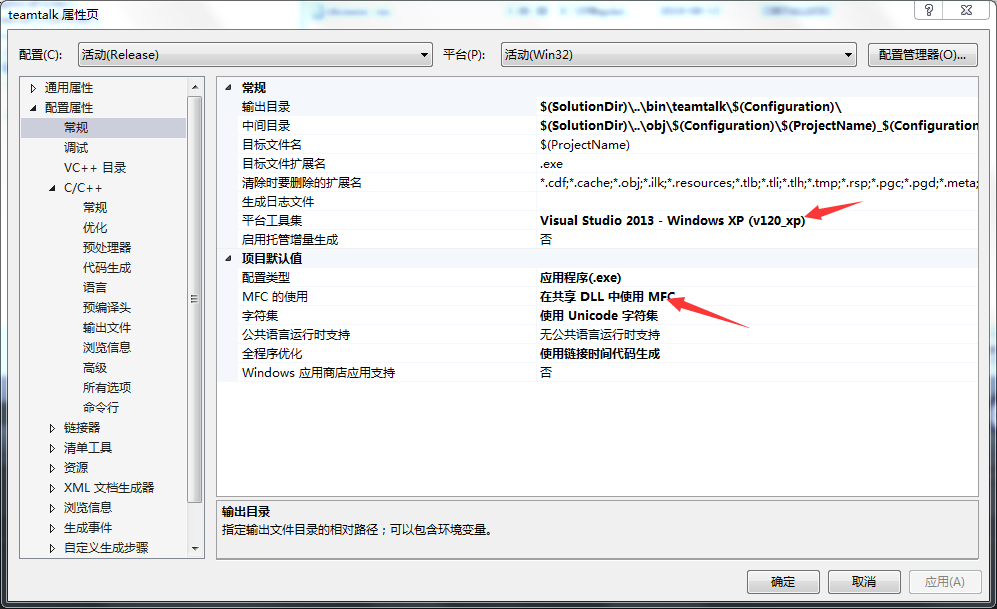
VS2013打包teamtalk
1 2. 如果是第一次打包的话,需要下载Installshield,按需下载,第二次打开就是我这样了 3. 4.修改图中箭头的地方,其他看你需求修改
5.因为teamtalk要用到.net4.5 6.重点!!!
首先点击addfolde…
teamtalk mysql.h_TeamTalk安装测试
TeamTalk介绍 项目框架 TeamTalk是蘑菇街的开源项目,github维护的最后时间是2015但是仍然是一款值得学习的好项目,麻雀虽小五脏俱全,本项目涉及到多个平台、多种语言,简单关系如下图 服务端: CppServer:TTC…
TeamTalk消息协议
数据通讯格式封装协议 Protocol Buffer
常用序列化方案比较 参考
https://www.cnblogs.com/johnny666888/p/12841735.html
Protocol Buffer
Protocol Buffer还有一个非常重要的优点就是可以保证同一消息报文新旧版本之间的兼容性
protobuf协议核心思想 基于128bits的数…
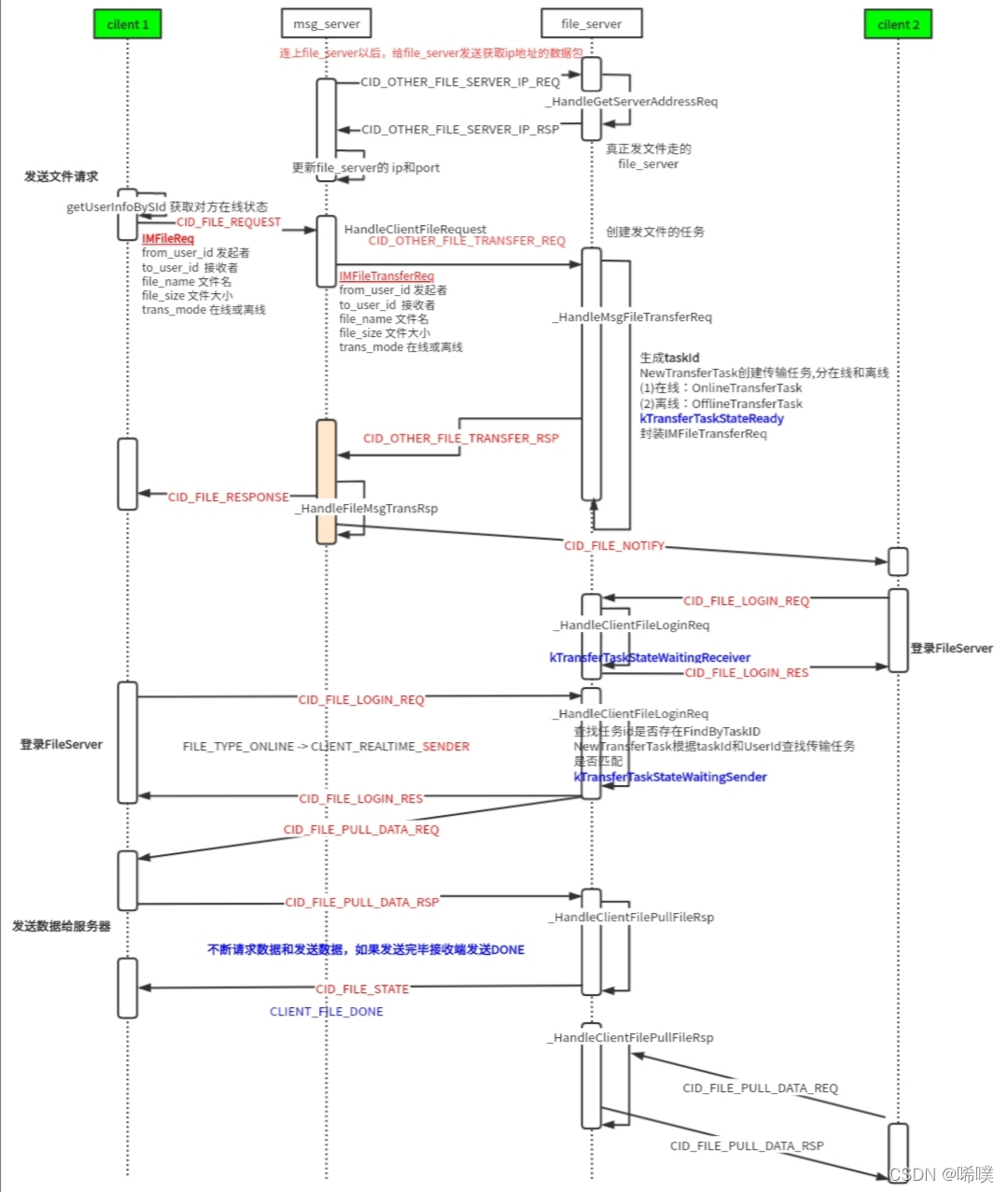
TeamTalk源码分析(1)
一、TeamTalk服务器端以下部署程序:
db_proxy_server、file_server、http_msg_server、login_server、msfs、msg_server、push_server、router_server 各个服务程序的作用描述如下:
LoginServer (C): 负载均衡服务器,分配一个负载小的MsgSe…
把TeamTalk(即时通讯项目)中的线程池连接池拆出来单独测试。
研究过Teamtalk的伙伴会发现它的线程池和连接池与很多文件有关联, 这篇文章主要写,把它的线程池连接池拆出来需要用到哪些文件。 其实我本来只想测试它的连接池的,但发现连接池里套的有线程池,于是就一起拆出来了。
整个工程的树…
teamtalk原理
再贴一遍架构图 从图中可以看出,对外使用的是http连接,内部使用的是tcp长连接。 类的命名规则:xxxServConn是模块连别的模块,xxxConn是别的模块连它。
协议设计
teamtalk采用protobuf进行序列化
typedef struct {uint32_t le…
TeamTalk源码分析(一)—— TeamTalk介绍
TeamTalk是蘑菇街开源的一款企业内部用的即时通讯软件(Enterprise IM),类似腾讯的RTX。网上也有很多的介绍,我这里也有写几遍关于这款产品的“流水账”,一方面对自己这段时间的阅读其代码做个总结,尽量做个…
teamtalk实现即时通讯
即时通讯技术应用非常广泛,涉及教育、电商、金融、泛娱乐、生活服务、医疗健康、政企服务、游戏聊天、在线客服等等行业,不是大家认为仅仅是qq、微信那样。
即时通讯架构
先给张图 客户端与服务器端进行网络通信、收发消息连接层为客户端收发消息提供…
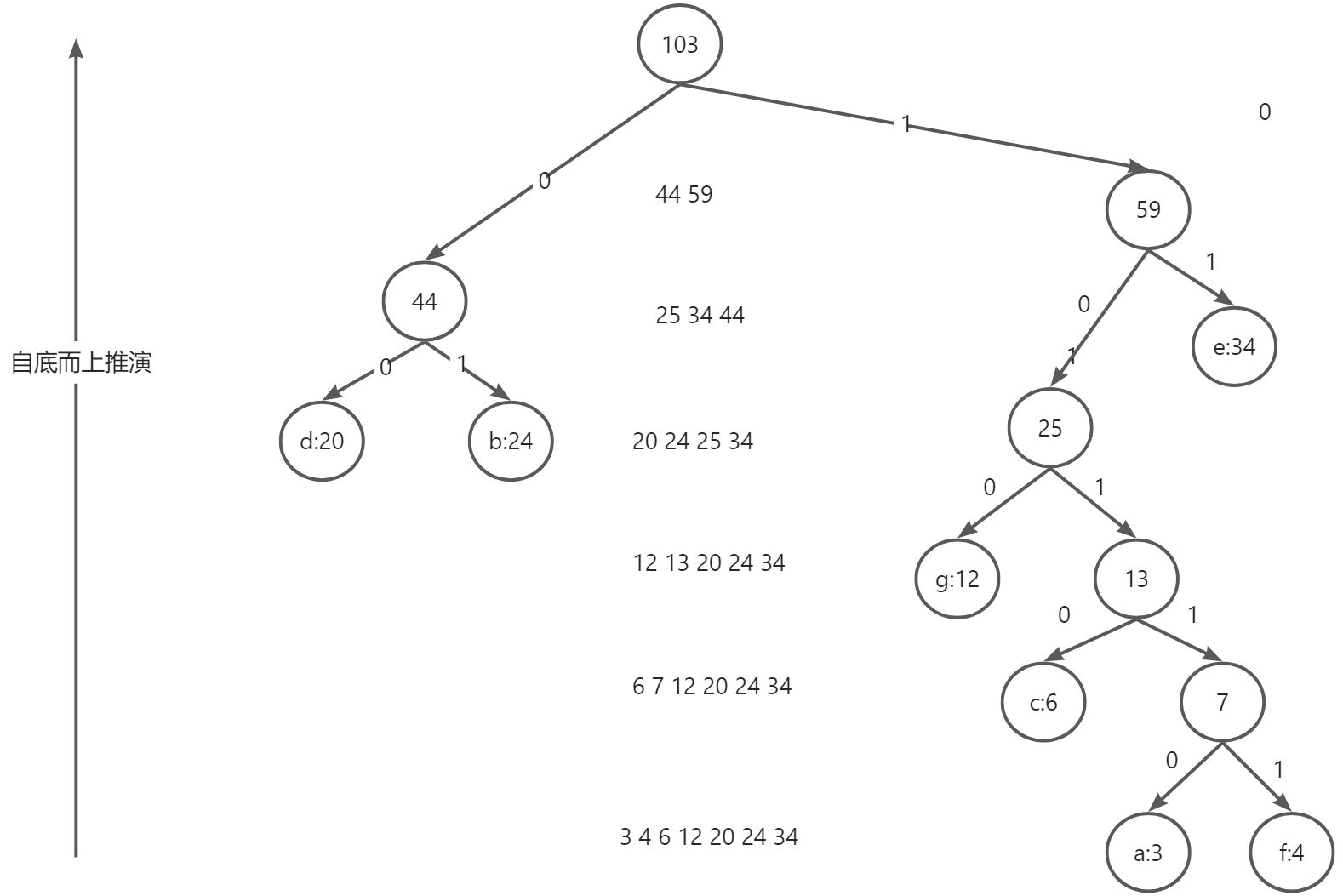
通识哈夫曼树及其应用,一起来构造属于自己的哈夫曼树
1.哈夫曼树的背景 哈夫曼(霍夫曼、赫夫曼)David Albert Huffman(August9,1925-October7,1999)。计算机科学的先驱,以他的哈夫曼编码闻名,在他的一生中,对于有限状态自动机,开关电路,异步过程和信…
哈佛结构冯·诺依曼结构
哈佛结构是一种将程序指令存储和
数据存储分开的存储器结构。哈佛结构是 一种并行体系结构,它的主要特点是将程序和数据存储在不同的存储空间中,即程序存储器和数据存储器是两个独立的存储器,每个存储器独立编址、独立访问。 冯诺依曼结构也…
微型计算机之哈佛架构是什么?
“哈佛体系结构”指的是什么?
微型计算机处理命令和数据,但是在很久以前的微型计算机中,用命令和数据共享了一条总线。在这种情况下,CPU在读取指令时使用总线,因此无法访问数据,并且在读取指令结束后访问数…
冯诺依曼结构、哈佛结构、改进型哈佛结构
冯诺依曼结构
冯诺依曼结构,又称为普林斯顿体系结构,是一种将程序指令存储器和数据存储器合并在一起的存储器结构。取指令和取操作数都在同一总线上,通过分时复用的方式进行;缺点是在高速运行时,不能达到同时取指令和…
高级数据结构之赫夫曼树
思考两个问题
电报发送:二战的时候大家都知道那时候普遍会应用电报,如果让你来设计一个电报的发送编码你该如何设计呢? 电报加密后越短越好,发送快。破解难解码容易换加密树也要快可逆的 压缩算法:给你10000个字符&am…
ARM到底是冯诺依曼结构还是哈佛结构?
问题 嵌入式的学习中ARM处理器是主题,这些年产业界除了PC和服务器市场外,以手机、pad、家电控制等为代表的嵌入式领域都被ARM几乎垄断了。所以学习嵌入式处理器,其实等同于学习ARM。(当然了,近两年RISC-V架构横空出世在…
冯诺依曼结构和哈佛结构的区别
冯诺依曼结构和哈佛结构的区别
1. 冯诺依曼结构:
说明:
一种将程序指令存储器和数据存储器合并在一起的存储器结构。程序指令存储地址和数据存储地址指向同一个存储器的不同物理位置,因此程序指令和数据的宽度相同。 冯诺依曼的计算机必须…