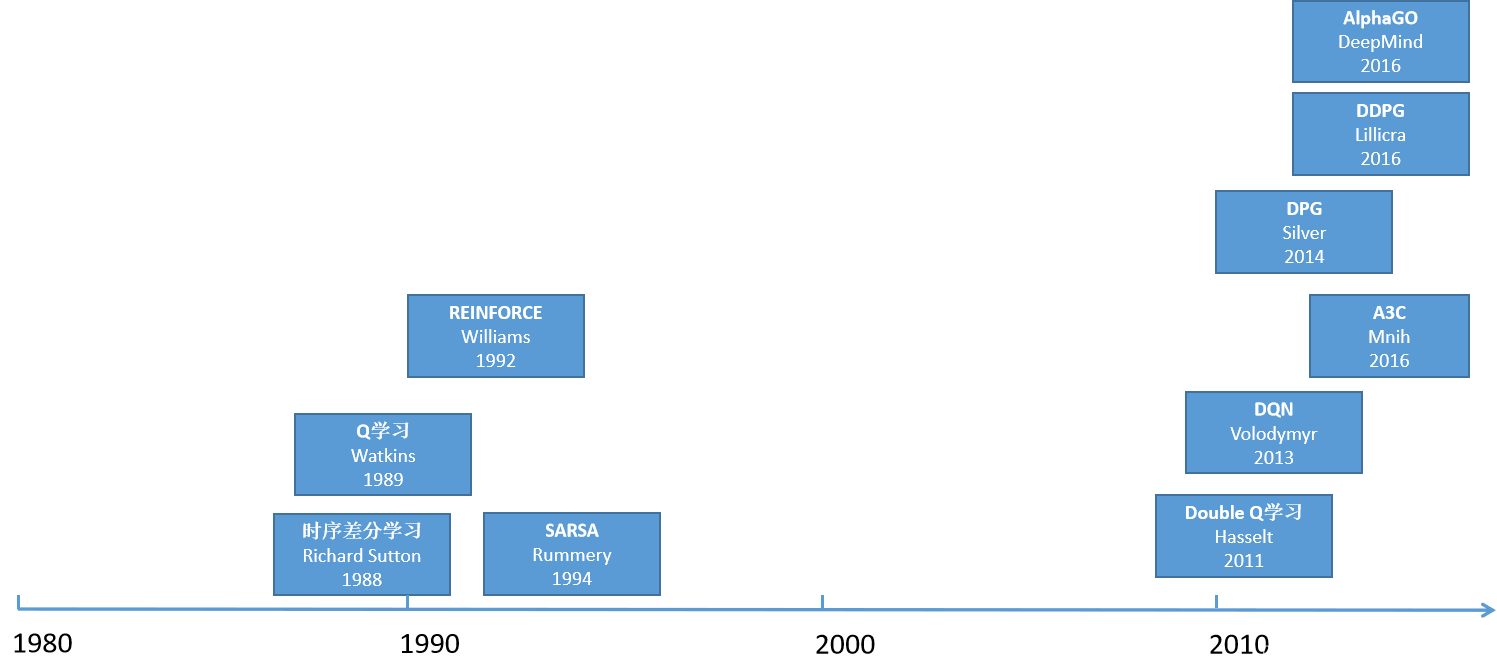
PCA:主成分分析(无监督)
PCA(Principal Component Analysis)是一种常用的数据降维技术,用于将多维数据集投影到低维空间中,同时保留数据的重要信息。PCA 的目标是在保持最大方差的同时,找到最佳的线性组合来表示数据。
以下是 PCA 的详细步骤:
1.数据标准化
在应用 PCA 之前,需要将数据标准化,使得每个特征的平均值为 0,方差为 1。这是因为 PCA 是基于方差计算的,如果某个特征的方差值过大,将会对结果产生较大的影响。
2.计算协方差矩阵
协方差矩阵反映了不同特征之间的相关性。通过计算协方差矩阵,可以找到数据中的主要方向。
3.计算特征值和特征向量(除了基于特征值分解,还可以SVD分解)
协方差矩阵的特征向量代表了数据的主要方向,特征值代表了数据在该方向上的重要性。通过计算协方差矩阵的特征值和特征向量,可以得到数据的主成分。
4.选择主成分
选择主成分的方法通常是基于特征值的大小。将特征值从大到小排序,选择前 k 个主成分,使得它们可以解释数据中的大部分方差。
5.计算投影矩阵
投影矩阵是将数据从高维空间投影到低维空间的矩阵。它的列向量是选择的主成分。
6.将数据投影到低维空间
通过将数据乘以投影矩阵,可以将数据投影到低维空间。在新的低维空间中,数据的每个样本可以表示为一个 k 维向量,其中 k 是选择的主成分的数量。
PCA 是一种非常有用的数据降维技术,可以帮助我们在保留数据重要信息的同时,减少数据的维度。在机器学习和数据分析中,PCA 经常被用作数据预处理步骤,以减少计算量并提高模型的效率。
SVD奇异值分解
SVD(Singular Value Decomposition)分解是一种常用的矩阵分解方法,可以将一个 m×n 的矩阵 A 分解为三个矩阵的乘积:U、S 和 V^T。其中,U 和 V^T 是正交矩阵,S 是对角矩阵。SVD 分解可以用于数据降维、矩阵压缩和矩阵近似等方面。
以下是 SVD 分解的详细步骤:
1.给定一个 m×n 的矩阵 A
2.计算 A^T × A 的特征值和特征向量
由于 A^T × A 是一个对称矩阵,因此可以计算它的特征值和特征向量。特征值按照从大到小的顺序排列,特征向量也相应地排列。
3.计算 V 矩阵
将 A^T × A 的特征向量作为 V 矩阵的列向量。由于特征向量是正交的,因此 V 是一个正交矩阵。
4.计算 A × A^T 的特征值和特征向量
同样地,可以计算 A × A^T 的特征值和特征向量。特征值按照从大到小的顺序排列,特征向量也相应地排列。
5.计算 U 矩阵
将 A × A^T 的特征向量作为 U 矩阵的列向量。由于特征向量是正交的,因此 U 是一个正交矩阵。
6.计算对角矩阵 S
对角矩阵 S 的对角线元素是 A × A^T 或 A^T × A 的特征值的平方根。由于特征值已按从大到小的顺序排列,因此对角线上的元素也应按相同的顺序排列。
7.重构原始矩阵
可以使用 U、S 和 V^T 重构原始矩阵。原始矩阵可以表示为 A = U × S × V^T。
SVD 分解的应用非常广泛,特别是在机器学习、数据挖掘和图像处理等领域。例如,在图像处理中,可以使用 SVD 分解将图像压缩为更小的矩阵,以便更轻松地存储和传输。在机器学习中,SVD 分解可以用于数据降维
SVM支持向量机
【机器学习】支持向量机 SVM(非常详细) - 知乎 (zhihu.com)
SVM 为什么要从原始问题变为对偶问题来求解
1.首先是我们有不等式约束方程,这就需要我们写成min max的形式来得到最优解。而这种写成这种形式对x不能求导,这种形式只能对a求导,所以我们需要转换成max min的形式,这时候,x就在里面了,这样就能对x求导了。而为了满足这种对偶变换成立,就需要满足KKT条件(KKT条件是原问题与对偶问题等价的必要条件,当原问题是凸优化问题时,变为充要条件)。
2.对偶问题将原始问题中的约束转为了对偶问题中的等式约束
3.方便核函数的引入
3. 改变了问题的复杂度。由求特征向量w转化为求比例系数a,在原始问题下,求解的复杂度与样本的维度有关,即w的维度。在对偶问题下,只与样本数量有关。

KNN
KNN分类算法:对于一个需要预测的输入向量x,我们只需要在训练数据集中寻找k个与向量x最近的向量的集合,然后把x的类别预测为这k个样本中类别数最多的那一类。
与分类预测类似,KNN算法用于回归预测时,同样是寻找新来的预测实例的k近邻,然后对这k个样本的目标值去均值即可作为新样本的预测值
梯度消失
梯度消失是指在神经网络的反向传播过程中,由于梯度在每一层中都要进行乘法运算,当梯度小于1时,经过多层传播后,梯度会不断缩小,最终变得非常小,导致前面的层无法更新,影响网络的训练效果。梯度消失的问题主要出现在深度神经网络中,特别是在使用sigmoid等激活函数时更加明显。
改善方法:
(1)使用不同的激活函数,如ReLU、LeakyReLU等,可以有效地减少梯度消失的问题。
(2)使用Batch Normalization,对每一层的输入进行标准化,可以使得输入分布更加稳定,有利于网络的训练。
(3)使用残差连接,可以使得网络更加深层,同时减少梯度消失的问题。
梯度爆炸
梯度爆炸是指在神经网络的反向传播过程中,由于梯度在每一层中都要进行乘法运算,当梯度大于1时,经过多层传播后,梯度会不断增大,最终变得非常大,导致参数更新过大,网络无法收敛。
改善方法:
(1)使用梯度裁剪,限制梯度的大小,可以有效地避免梯度爆炸的问题。
(2)使用更加合理的初始化方法,如Xavier、He等,可以使得参数初始化更加合理,有利于网络的训练。
(3)使用Batch Normalization,对每一层的输入进行标准化,可以使得输入分布更加稳定,有利于网络的训练。

决策树:






集成学习:
通常来说,生成一个完整的集成学习算法的步骤可以大致分为以下两步:
· 构建基学习器:生成一系列基学习器,这个过程可以是并行的(Parallel)也可以是顺序的(Sequential)(在顺序型的生成过程中,前期生成的基学习器会对后续生成的学习器有影响)
· 组合基学习器:这些基学习器被组合起来使用,最常见的组合方法比如用于分类的多数投票(majority voting),以及用于回归的权重平均(weighted averaging)。
·
· 平行方法:
· 构建多个独立的学习器,取他们的预测结果的平均
· 个体学习器之间不存在强依赖关系,一系列个体学习器可以并行生成
· 通常是同质的弱学习器
· 代表算法是Bagging和随机森林(Random Forest)系列算法。
·
· 顺序化方法:
· 多个学习器是依次构建的
· 个体学习器之间存在强依赖关系,因为一系列个体学习器需要串行生成
· 通常是异质的学习器
· 代表算法是Boosting系列算法,比如AdaBoost,梯度提升树等
Adaboost:

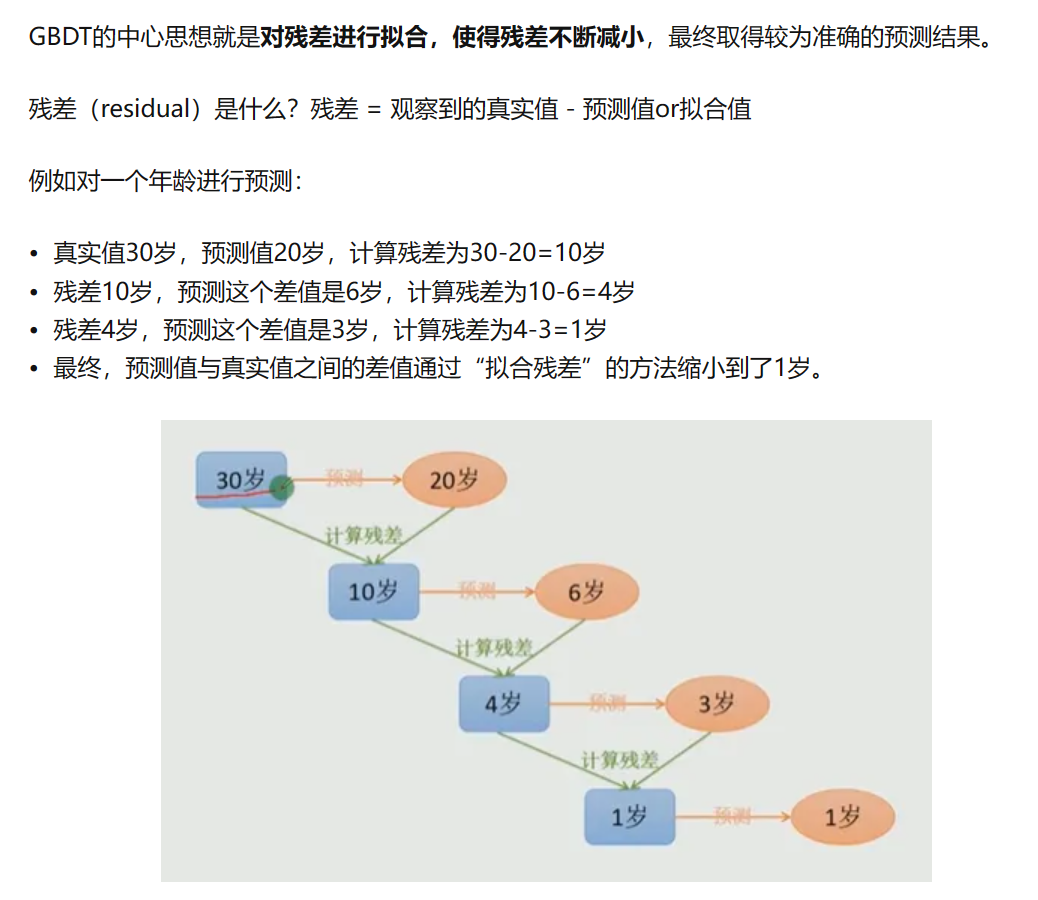
GBDT(梯度提升树),弱学习器限定了只能使用CART回归树模型



Xgboost:(极限梯度提升)