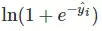机器学习：多分类

1，多分类形式化

1.1，分类问题

给定训练样本集合 $S=\left \{ (x_1,y_1),...,(x_m,y_m) \right \}$ ，其中 $\left \{ x_i \right \}^m_{i=1}\subseteq X ^m$ 独立同分布， $y_i=f(x_i)\in Y(\forall i=1,...,m)$ 。多分类问题的目标是基于数据 $S$ ，从假说集合 $H$ 中选择一个假说 $h$ ，以使得期望误差：

$E_{x\sim D}[sgn(h(x))\neq f(x)]$

最小。

对于二分类问题，可以以零为界限进行分类，大于零则划分为正样本，小于零则划分为负样本。对于多分类问题，二分类分类方法则无法进行判断，因此我们定义评分函数进行判断。

在多类设置中，根据评分函数 $h$ 定义假设： $h:X*Y\rightarrow R$ 。与点 $x$ 关联的标签是导致最大分数 $h(x,y)$ 的标签，该分数定义了以下映射： $x$ 到 $y$ ：

$x \mapsto arg\, \, \, \underset{y\in Y}{max}(h(x,y))$

其中 $Y = \left \{ y_1,y_2,y_3,..,y_n \right \}$ ，其中每个 $y_i$ 都是一种类别，通过遍历所有的 $y_i$ 与待预测值 $x$ 通过评分函数 $h(x,y)$ 进行计算得分，得分最高的 $y_i$ 即为 $x$ 的多分类结果。

1.2，多分类SVMs

机器学习：支持向量机（SVM）_燕双嘤-CSDN博客1，算法描述支持向量机（SVM）是用来解决分类问题的。作为数据挖掘领域中一项非常重要的任务，分类目前在商业上应用最多（比如分析型CRM里面的客户分类模型、客户流失模型、客户盈利等，其本质上都属于分类问题）。而分类的目的则是构造一个分类函数或分类模型，该模型能吧数据库中的数据项映射到给定类别中的某一个，从而可以用来预测未知类别。先考虑最简单的情况，比如豌豆和米粒，用筛子很快可以分离它们，小颗粒漏下去，大颗粒保留。用函数来表示就是当直径d大于某个值D，就判定其为豌豆，小于D就是米粒。在数轴上就是D左边https://shao12138.blog.csdn.net/article/details/121164645定义多分类SVM算法（SVMs）的优化问题是：

$\underset{W,\xi }{min}\left [ \frac{1}{2}\sum_{l=1}^{k}||w_l||^2+C\sum_{i=1}^{m} \xi_i\right ]$

$s.t.\, \, \, \, \forall i\in [1,m],\forall l\in Y-\left \{ y_i \right \},w_{y_i}*\Phi (x_i)\geqslant w_l*\Phi(x_i)+1-\xi_i$

$\xi_i \geqslant 0\, \, \, \, i=1,2,...,m$

其中 $\Phi (x_i)$ 为 $x_i$ 到 $H$ 的映射函数， $w_{y_i}$ 为当前 $x_i$ 分类正确的系数矩阵，

$w_l$ 为除 $w_{y_i}$ 之外的任意一个 $w$ ， $\xi_i$ 为偏差，

$m$ 为样本数， $k$ 为分类数。

$w_{y_i}*\Phi (x_i)\geqslant w_l*\Phi(x_i)+1-\xi_i$

证明：

$h(x_i,y_i)-h(x_i,y)\geqslant \tau$

令， $h(x_i,y_i)=w^T_{y_i}*x_i$ ，评分函数有无数种。

$w^T_{y_i}*x_i-w^T_y*x_i\geqslant \tau$

$\frac{w^T_{y_i}}{\tau}*x_i-\frac{w^T_{y}}{\tau}*x_i\geqslant 1$

令 $m^T_{y_i}=\frac{w^T_{y_i}}{\tau}$ ，即：

$m^T_{y_i}*x_i-m^T_y*x_i\geqslant1$

1.3，对偶问题

机器学习：支持向量机（SVM）_燕双嘤-CSDN博客1，算法描述支持向量机（SVM）是用来解决分类问题的。作为数据挖掘领域中一项非常重要的任务，分类目前在商业上应用最多（比如分析型CRM里面的客户分类模型、客户流失模型、客户盈利等，其本质上都属于分类问题）。而分类的目的则是构造一个分类函数或分类模型，该模型能吧数据库中的数据项映射到给定类别中的某一个，从而可以用来预测未知类别。先考虑最简单的情况，比如豌豆和米粒，用筛子很快可以分离它们，小颗粒漏下去，大颗粒保留。用函数来表示就是当直径d大于某个值D，就判定其为豌豆，小于D就是米粒。在数轴上就是D左边https://shao12138.blog.csdn.net/article/details/121164645

$\underset{W,\xi }{min}\left [ \frac{1}{2}\sum_{l=1}^{k}||w_l||^2+C\sum_{i=1}^{m} \xi_i\right ]$

$s.t.\, \, \, \, \forall i\in [1,m],\forall l\in Y-\left \{ y_i \right \},w_{y_i}*\Phi (x_i)\geqslant w_l*\Phi(x_i)+1-\xi_i$

$\xi_i \geqslant 0\, \, \, \, i=1,2,...,m$

定义拉格朗日函数

$L(w,\alpha ,\xi ,\beta )=\frac{1}{2}\sum_{l=y_1,l\neq y_i}^{y_k}||w_l||^2+C\sum_{i=1}^{m} \xi_i+\sum_{i=1}^{m}\sum_{l=y_1,l\neq y_i}^{y_k}\alpha_{il}[1-\xi _i- w^T_{y_i}\Phi(x_i) +w^T_l\Phi(x_i)]-\sum_{i=1}^{m}\beta_i\xi _i$

令 $L(w,\alpha ,\xi ,\beta )$ 对 $w,\xi$ 求偏导为0可得：

$\frac{\partial L}{\partial w_l}=0\rightarrow \sum_{l=y_1,l\neq y_i}^{y_k}w_l +\sum_{i=1}^{m}\sum_{l=y_1,l\neq y_i}^{y_k}\alpha_{il}\Phi(x_i)=0$

$\frac{\partial L}{\partial \xi_i }=0\rightarrow \sum_{i=1}^{m}C+\sum_{i=1}^{m}[\sum_{l=y_1,l\neq y_i}^{y_k}\alpha_{il}-\beta_i]=0$

带入拉格朗日函数，可以消除 $w$ ，再消去 $\beta_i$ 得到对偶问题：

$=\frac{1}{2}\sum_{l=y_1,l\neq y_i}^{y_k}||w_l||^2+\sum_{i=1}^{m}\sum_{l=y_1,l\neq y_i}^{y_k}\alpha_{il}[1- w^T_{y_i}\Phi(x_i) +w^T_l\Phi(x_i)]+C\sum_{i=1}^{m} \xi_i-\sum_{i=1}^{m}\sum_{l=y_1,l\neq y_i}^{y_k}\alpha_{il}\xi _i-\sum_{i=1}^{m}\beta_i\xi _i$

$=\frac{1}{2}\sum_{l=y_1,l\neq y_i}^{y_k}||w_l||^2+\sum_{i=1}^{m}\sum_{l=y_1,l\neq y_i}^{y_k}\alpha_{il}[1- w^T_{y_i}\Phi(x_i) +w^T_l\Phi(x_i)]$

$=\frac{1}{2}\sum_{l=y_1,l\neq y_i}^{y_k}w^T_lw_l+\sum_{i=1}^{m}\sum_{l=y_1,l\neq y_i}^{y_k}\alpha_{il}[1- w^T_{y_i}\Phi(x_i) +w^T_l\Phi(x_i)]$

$=\frac{1}{2}\sum_{l=y_1,l\neq y_i}^{y_k}w^T_lw_l-\sum_{i=1}^{m}\sum_{l=y_1,l\neq y_i}^{y_k}\alpha_{il}[w^T_{y_i}\Phi(x_i) -w^T_l\Phi(x_i)]+\sum_{i=1}^{m}\sum_{l=y_1,l\neq y_i}^{y_k}\alpha_{il}$

$=\frac{1}{2}\sum_{l=y_1,l\neq y_i}^{y_k}w^T_lw_l-\sum_{i=1}^{m}\sum_{l=y_1,l\neq y_i}^{y_k}\alpha_{il}w^T_{y_i}\Phi(x_i) +\sum_{i=1}^{m}\sum_{l=y_1,l\neq y_i}^{y_k}\alpha_{il}w^T_l\Phi(x_i)+\sum_{i=1}^{m}\sum_{l=y_1,l\neq y_i}^{y_k}\alpha_{il}$

$=-\frac{1}{2}\sum_{i=1}^{m}\sum_{l=y_1,l\neq y_i}^{y_k}\alpha_{il}\Phi(x_i)w^T_l-\sum_{i=1}^{m}\sum_{l=y_1,l\neq y_i}^{y_k}\alpha_{il}w^T_{y_i}\Phi(x_i) +\sum_{i=1}^{m}\sum_{l=y_1,l\neq y_i}^{y_k}\alpha_{il}w^T_l\Phi(x_i)+\sum_{i=1}^{m}\sum_{l=y_1,l\neq y_i}^{y_k}\alpha_{il}$

$=\frac{1}{2}\sum_{i=1}^{m}\sum_{l=y_1,l\neq y_i}^{y_k}\alpha_{il}\Phi(x_i)w^T_l-\sum_{i=1}^{m}\sum_{l=y_1,l\neq y_i}^{y_k}\alpha_{il}w^T_{y_i}\Phi(x_i) +\sum_{i=1}^{m}\sum_{l=y_1,l\neq y_i}^{y_k}\alpha_{il}$

$=\sum_{i=1}^{m}\sum_{l=y_1,l\neq y_i}^{y_k}\alpha_{il}\Phi(x_i)[\frac{1}{2}w^T_l-w^T_{y_i}]+\sum_{i=1}^{m}\sum_{l=y_1,l\neq y_i}^{y_k}\alpha_{il}$

即： $\underset{\alpha }{max}[\sum_{i=1}^{m}\sum_{l=y_1,l\neq y_i}^{y_k}\alpha_{il}\Phi(x_i)[\frac{1}{2}w^T_l-w^T_{y_i}]+\sum_{i=1}^{m}\sum_{l=y_1,l\neq y_i}^{y_k}\alpha_{il}]$

假设 $\alpha ^{*}$ 是上面凸二次规划问题的最优解，则 $\alpha ^{*}\neq 0$ ，求导后得到 $\alpha ^{*}$ 。

2，二分类解决多分类

2.1，两种多分类策略

One-versus-All：每次将一个类别作为正类，其余类别作为负类。此时共有（N个分类器）。在测试的时候若仅有一个分类器预测为正类，则对应的类别标记为最终的分类结果。

【例】当有4个类别的时候，每次把其中一个类别作为正类别，其余作为负类别，共有4种组合，对于这4中组合进行分类器的训练，我们可以得到4个分类器。对于测试样本，放进4个分类器进行预测，仅有一个分类器预测为正类，于是取这个分类器的结果作为预测结果，分类器2预测的结果是类别2，于是这个样本便属于类别2。

One-versus-One：假如某个分类中有N个类别，我们将这N个类别进行两两配对（两两配对后转化为二分类问题）。那么我们可以得到 $C^2_N$ ，即 $\frac{N(N-1)}{2}$ 。

【例】当有4个类别的时候，首先把类别两两组合（6种组合）。组合完之后，其中一个类别作为正类，另一个作为负类（这个正负只是相对而言，目的是转化为二分类）。然后对每个二分类器进行训练。可以得到6个二分类器。然后把测试样本在6个二分类器上面进行预测。

容易看出，OvA只需训练N个分类器，而OvO需训练N(N - 1)/2个分类器，因此，OvO的存储开销和测试时间开销通常比OvA更大。但在训练时，OvA的每个分类器均使用全部训练样例，而OvO的每个分类器仅用到两个类的样例，因此，在类别很多时，OvO的训练时间开销通常比OvA更小。至于预测性能，则取决于具体的数据分布，在多数情形下OvA准确度比OvO要低，比如10000样本集，分给OvA的100个分类器，每个得到100个样本，对于1:99的分类器，正样本仅有100，负样本有9900，样本极不平衡，训练误差较大。

综上：

OvO的优点是，在类别很多时，训练时间要比OvA少，误差小。缺点是，分类器个数多。
OvA的优点是，分类器个数少，存储开销和测试时间比OvO短。缺点是，类别很多时，训练时间长，误差大。

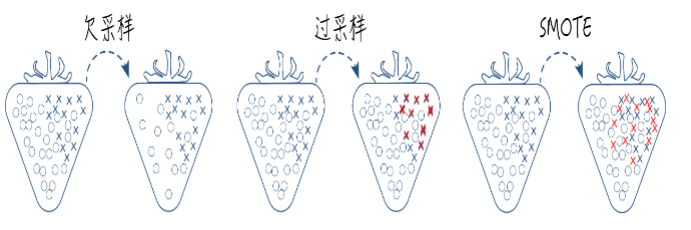
2.2，不平衡数据处理

数据不平衡是指数据集中各类样本数量不均衡的情况。常用不平衡处理方法有采样和代价敏感学习。

采样：欠采样、过采样和综合采样的方法。

代价敏感学习：代价敏感学习是指为不同类别的样本提供不同的权重，从而让机器学习模型进行学习的一种方法。

比如风控或者入侵检测，这两类任务都具有严重的数据不平衡问题，可以在算法学习的时候，为少类样本设置更高的学习权重，从而让算法更加专注于少类样本的分类情况，提高对少类样本分类的查全率，但是也会将很多多类样本分类为少类样本，降低少类样本分类的查准率。

2.3，多分类器

其中第一列为多分类的类别 $K$ ，第一行为多个分类器，可以是SVM，PAL等。

每一行不能线性相关，即不能相互表示；每一列不能全是0或1。

OvO和OvA是多分类器的一种特例。

我们根据每个二分类器的分类结果，对比 $M$ 矩阵中的形式的分类，进行确认。

通常采用：汉明距离（不同+1，相同+0）。

2.4，如何学习 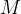$M$

学习 $M$ 的算法类似于刚才在多类支持向量机中讨论的思想，其公式如下：

$\underset{M,\xi }{min}||M||^2_F+C\sum_{i=1}^{m}\xi_i$

$s.t.\, \, \, \, \forall i\in [1:m]\forall l\in Y-\left \{ y_i \right \}$

$K(M_{yi},F(x_i))-K(M_l,F(x_i))\geqslant 1-\xi_i,\xi_i\geqslant 0$

其中， $F(x_i)$ 表示在多个二分器中得到的01序列，

$K(M_{yi},F(x_i))$ 表示在矩阵 $M$ 中的汉明距离。

求解方法：结构化预测

上述问题可以写成：

$\left \{ (x_i,y_i) \right \}^m_i=1\overset{M}{\rightarrow }\left \{ (F(x_i),y_i) \right \}^m_i$

进而

$\xi_{iy}\geqslant 1-K(M_{yi},F(x_i))-K(M_l,F(x_i))$

$\geqslant 1-[w^T\Phi (x_i,y_i)-w^T\Phi(x_i,y)]$

$\xi_{iy}=max\left \{ 0,1-[w^T\Phi (x_i,y_i)-w^T\Phi(x_i,y)] \right \}$

故开始问题等价于：

$\underset{W,\xi }{min}\left [ \frac{1}{2}||w_l||^2+C\sum_{i=1}^{m}\underset{y\neq y_i}{max}[max\left \{ 0,1-[w^T\Phi (x_i,y_i)-w^T\Phi(x_i,y)] \right \}\right ]$

由于max max不好求，我们可以转换为指数形式再求对数：

$\underset{W,\xi }{min}\left [ \frac{1}{2}||w_l||^2+C\sum_{i=1}^{m}log\sum_{y\in Y}^{}[exp\left \{ L(y_i,y)-[w^T\Phi (x_i,y_i)-w^T\Phi(x_i,y)] \right \}\right ]$

其中， $L(y_i,y)$ 为损失函数，取0-1损失函数(zero-one loss)。