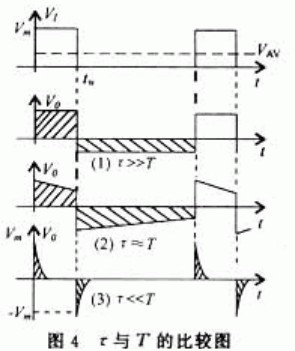
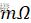一、高通电路

 1.1传输特性

  $A_u$ = $\frac{R}{R+\frac{1}{j\omega C}}$
  （补充知识：j是复数域中的一个旋转因子）

  详细求解思路：
  求解$A_u$就是要求输入与输出的关系。

  所以$A_u$ = $\frac{{\dot{U}}_o}{{\dot{U}}_i}$ = $\frac{\dot{I}R}{\dot{I}(-j{X}_{{}_C}+R)}$ = $\frac{R}{-j{X}_{{}_C}+R}$ = $\frac{R}{-j\frac{1}{\omega C}+R}$ =   $\frac{R}{R+\frac{1}{j\omega C}}$

  (因为电容的电压滞后电阻的电压90°，所以是-j；$\dot{I}$是流过电容和电阻的电流)

  (电容容抗的公式为 $X_C$ = $\frac{1}{2\pi fC}$ = $\frac{1}{\omega C}$， 其中$\omega$ = $2\pi f$)
 

 1.2 幅频响应（放大倍数和频率之间的关系）

  |$A_u$| = $F(f)$，$A_u$ = $\frac{1}{1+\frac{1}{j\omega RC}}$
 

 1.3下限截止频率：$f_{{}_L}$（补充知识：下限截止频率：衰减到最大值的$\frac{1}{\sqrt{2}}$）

  ${\omega }_{{}_L}RC$ = 1 $\Rightarrow$ ${\omega }_{{}_L}$ = $\frac{1}{RC}$ $\Rightarrow$ $2\pi f_{{}_L}$ = $\frac{1}{RC}$ $\Rightarrow$ $f_{{}_L}$ = $\frac{1}{2\pi RC}$
 

  所以得到标准形式：
  $A_u$ = $\frac{1}{1+\frac{1}{j\omega RC}}$ = $\frac{j\frac{f}{f_{{}_L}}}{1+j\frac{f}{f_{{}_L}}}$

 

二、低通电路

 2.1传输特性

  $A_{{}_u}$ = $\frac{1}{1+j\omega RC}$
 

 2.2 上限截止频率：$f_{{}_H}$

  $A_u$ = $\frac{1}{1+\frac{f}{f_{{}_H}}}$
  (推导公式，如上面高通电路一样推导)
 

 2.3电压随时间变化曲线

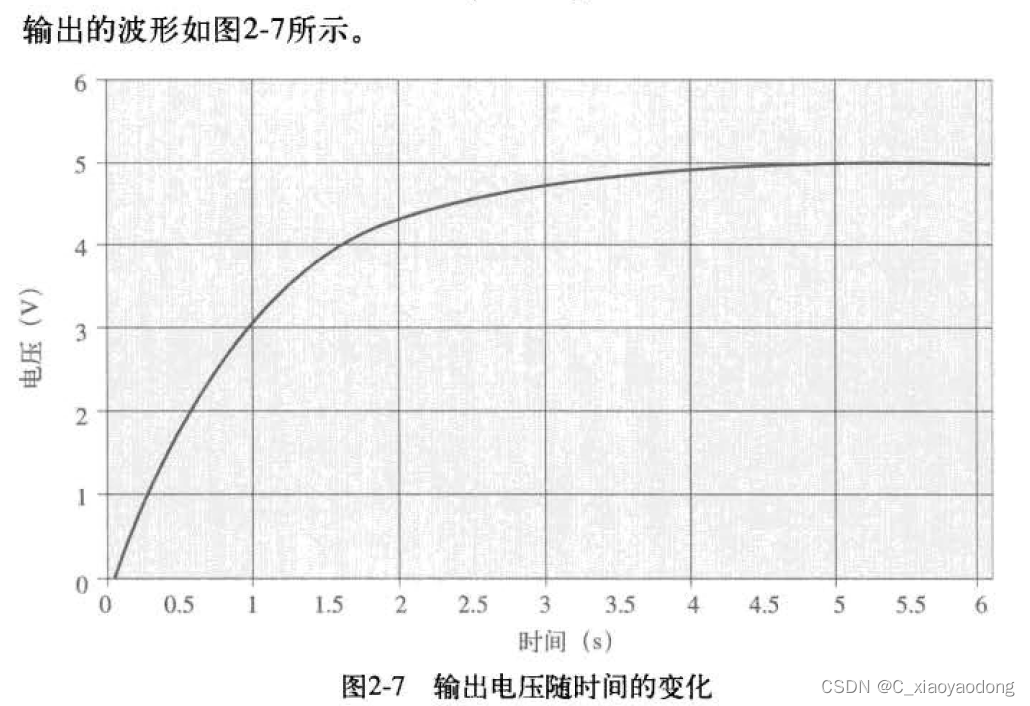
（用分压的思想，绘制上面图，不要用定义式，要用欧姆定律的实质）
 
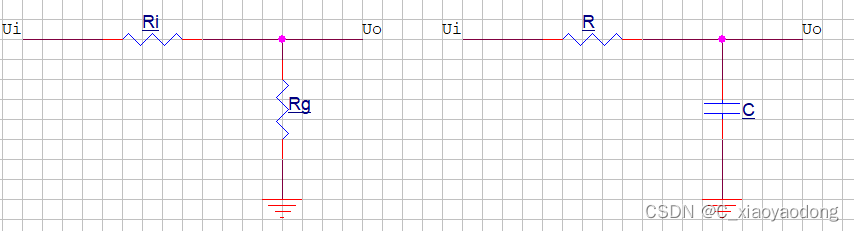
将Rg替换成电容C，就变成了右边的电路，其实质也是两个电阻的分压，
只是方式不同，因为电容C会随频率而改变其阻抗。

绘制电压变化曲线思路：（前提频率(f)是由高到低，需要参考两电阻分压的思路，来对比RC电路）
$f$ : 高 $\to$ 低 $\Rightarrow$ $X_c$ $\uparrow$(上升) $\Rightarrow$ $U_o$ $\uparrow$(上升)
 

三、总结

 耦合电容引起的电路是高通电路
 级间电容引起的电路是低通电路
 

参考资料

[1] 文章图片来自上海交通大学的郑益慧主讲的模电视频 https://www.bilibili.com/video/BV1Gt411b7Zq?p=23&vd_source=ed724b4f3ba41f99fa4b9e7a0a62dada
[2] 电压随时间变化曲线来自，电子电气工程师必知必会第2版. [美]Darren Ashby著, 尹华杰译