电路中一阶线性微分方程
在高等数学中,一阶微分方程求解过程需要先算出齐次的通解,然后再根据初始条件算出特解,计算与推理过程很是复杂。在我们学习电路的时候再遇到这个东西时,会因为之前复杂的求解方式严重打击自信心,加之老师说数学在电路中应用是非常广泛的,对于RC电路中存在这个一阶线性微分方程,已经成为拦路虎。
本文将从另一个角度讲解一阶微分方程在电路中的应用,让你感觉到数学在此次的RC电路中,充其量就是个计算方法的引荐或者是一个工具,电路中有一套自己的方法对待这个,而且解法固定,没有套路(态度真诚),只需知道一阶微分方程的基本概念是什么,比如一阶指的是啥,线性指的是啥,导数是啥。
解法介绍
分为两个步骤:求齐次的通解,然后请求非齐次的特解。
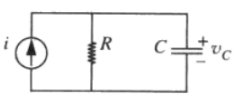
如上电路图,根据KCL,我们可以得出 i = C d v c d t + v c R i = C \frac{dv_c}{dt} + \frac{v_c}{R} i=Cdtdvc+Rvc 。
对上式子进行化简一下得出: i C = d v c d t + v c R C \frac{i}{C} = \frac{dv_c}{dt} + \frac{v_c}{RC} Ci=dtdvc+RCvc
通过上式可以知道, 1 R C \frac{1}{RC} RC1 是一个常数,该式是关于 v c v_c vc的一阶线性微分方程。所以需要求解出该方程的解,在RC电路中,一阶微分方程求解出来的解是一个函数,而不是一个值。
顺便提一下在Java开发中,语法中lambda表达式,这个表达就是把一个函数当成一个变量传递过去。在微分方程中,也可以顺着思路想一下,微分方程是导数的方程,那么原来的函数就是之前的解了,而不是常数值解。
先求齐次的通解
C d v c d t + v c R = i C \frac{dv_c}{dt} + \frac{v_c}{R} = i Cdtdvc+Rvc=i 式的齐次方程为: d v c d t + v c R C = 0 \frac{dv_c}{dt} + \frac{v_c}{RC} = 0 dtdvc+RCvc=0 。
这里电路没有套路做法体现出来了,齐次方程的通解为: v c = A e λ t v_c = Ae^{ \lambda t} vc=Aeλt 你没看错,通解就是这种固定的写法,压根都不用复杂推导。 然后求出该式中的 λ \lambda λ 值,对该式子求导,带入到齐次方程中去;
得出 λ A e λ t + 1 R C A e λ t = 0 \lambda Ae^{ \lambda t} + \frac{1}{RC} Ae^{ \lambda t} = 0 λAeλt+RC1Aeλt=0 。
化简可以得到 λ + 1 R C = 0 \lambda + \frac{1}{RC} = 0 λ+RC1=0 也就是 λ = − 1 R C \lambda = - \frac{1}{RC} λ=−RC1 。
齐次方程的通解为 v c = A e − t ⋅ 1 R C v_c = Ae^{ - t \cdot \frac{1}{RC}} vc=Ae−t⋅RC1 。
注:我们来看一下这个齐次方程,没有了 i i i,也就是没有图中的电流源,也就是没有了外界输入,变成下面这样的图。
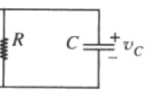
然后求非齐次特解(特解就是特定的解,一个指定的解)
本次例子中的式子是这种的 C d v c d t + v c R = i C \frac{dv_c}{dt} + \frac{v_c}{R} = i Cdtdvc+Rvc=i , i i i是一个常数;那么跟齐次方程的通解一样,可以立马得到 v c = A v_c = A vc=A,这里的A是一个常数变量。然后带入到非齐次方程中,得到 A = i R A = iR A=iR ,也就是特解是 v c = i R v_c = iR vc=iR。
最终的解为 齐次方程的通解 加上 非齐次方程的特解,所以 v c = − i R e − t ⋅ 1 R C + i R v_c = -iRe^{ - t \cdot \frac{1}{RC}} + iR vc=−iRe−t⋅RC1+iR 。
非齐次方程特解的一般推导
如果非齐次方程为 : d x ( t ) d t + x ( t ) R C = t \frac{dx(t)}{dt} + \frac{x(t)}{RC} = t dtdx(t)+RCx(t)=t,那么特解是 x ( t ) = B t + D x(t) = Bt + D x(t)=Bt+D,把 x ( t ) = B t + D x(t) = Bt + D x(t)=Bt+D 式子 带到 非齐次方程 里面去求出 B 和 D。
带入求解的方式如下:
-
根据 x ( t ) = B t + D x(t) = Bt + D x(t)=Bt+D 对其求导可得 d x ( t ) d t = B \frac{dx(t)}{dt} = B dtdx(t)=B ,带入非齐次方程中可得 B + B t + D R C = t B + \frac{Bt + D}{RC} = t B+RCBt+D=t ,得到式子 R C ⋅ B + B t + D = R C ⋅ t RC \cdot B + Bt + D =RC \cdot t RC⋅B+Bt+D=RC⋅t 整理可得 B = R C B = RC B=RC,可得 D = − ( R C ) 2 D = - (RC)^2 D=−(RC)2;
-
最终的非齐次方程的通解为 : A e − t ⋅ 1 R C + R C ⋅ t − ( R C ) 2 Ae^{ - t \cdot \frac{1}{RC}} + RC \cdot t - (RC)^2 Ae−t⋅RC1+RC⋅t−(RC)2 。
-
我们从最终的通解仍然没有得到A的未知数,解得A需要根据电路0时刻的条件,比如x(0)等于多少。
如果非齐次方程为 : d x ( t ) d t + x ( t ) R C = t 2 \frac{dx(t)}{dt} + \frac{x(t)}{RC} = t^2 dtdx(t)+RCx(t)=t2 那么特解是 x ( t ) = E t 2 + B t + D x(t) = Et^2 + Bt + D x(t)=Et2+Bt+D,解法跟上面一样,把 x ( t ) = E t 2 + B t + D x(t) = Et^2 + Bt + D x(t)=Et2+Bt+D式子 带到 非齐次方程 里面去求出E、B 和 D。
然后再加上齐次方程的通解。
图形表示
最终求解公式 v c = − i R e − t ⋅ 1 R C + i R v_c = -iRe^{ - t \cdot \frac{1}{RC}} + iR vc=−iRe−t⋅RC1+iR 做成图形;iR赋值成4、RC分为4 8 12、x是时间t。如下图我们可以看到RC越大,图形变道4的时间越长,所以RC的值是影响RC电路趋于稳定 i R iR iR值的唯一指标。
这个特性就是在RC时间范围内,电路在趋于稳态(稳定的状态,已经充完电了,电容相当于一个断路了)。

上图中的公式显示在下面,可以直接拷贝进去就可以显示了
4(1−𝑒^(−𝑥/4) )4(1−𝑒^(−𝑥/8) )4(1−𝑒^(−𝑥/12) )