Apriori算法
首先,Apriori算法是关联规则挖掘中很基础也很经典的一个算法。 转载来自:链接:https://www.jianshu.com/p/26d61b83492e
所以做如下补充:
关联规则:形如X→Y的蕴涵式,其中, X和Y分别称为关联规则的先导(antecedent或left-hand-side, LHS)和后继(consequent或right-hand-side, RHS) 。其中,关联规则XY,存在支持度和信任度。
置信度:在所有的购买了左边商品的交易中,同时又购买了右边商品的交易机率,包含规则两边商品的交易次数/包括规则左边商品的交易次数。
提升度:(有这个规则和没有这个规则是否概率会提升,规则是否有价值):无任何约束的情况下买后项的交易次数/置信度。注意:提升度必须大于1才有意义。
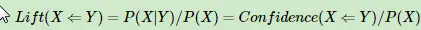
进入正题啦~
Apriori的算法思想
在Apriori算法z中,我们通常使用支持度来作为我们判断频繁项集的标准。
Apriori算法的目标是找到最大的K项频繁集。
补充:{频繁项集产生:其目标是发现满足最小支持度阈值的所有项集,这些项集称作频繁项集(frequent itemset)}
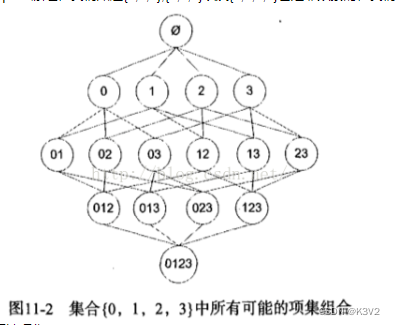
Apriori定律1:如果一个集合是频繁项集,则它的所有子集都是频繁项集。
举个栗子:假设一个集合{A,B}是频繁项集,即A、B同时出现在一条记录的次数大于等于最小支持度min_support,则它的子集{A},{B}出现次数必定大于等于min_support,即它的子集都是频繁项集。
Apriori定律2:如果一个集合不是频繁项集,则它的所有超集都不是频繁项集。
举个栗子:假设集合{A}不是频繁项集,即A出现的次数小于 min_support,则它的任何超集如{A,B}出现的次数必定小于min_support,因此其超集必定也不是频繁项集。
Apriori的算法步骤
输入:数据集合D,支持度阈值α
输出:最大的频繁k项集
1)扫描整个数据集,得到所有出现过的数据,作为候选频繁1项集。k=1,频繁0项集为空集。
2)挖掘频繁k项集
a) 扫描数据计算候选频繁k项集的支持度
b) 去除候选频繁k项集中支持度低于阈值的数据集,得到频繁k项集。如果得到的频繁k项集为空,则直接返回频繁k-1项集的集合作为算法结果,算法结束。如果得到的频繁k项集只有一项,则直接返回频繁k项集的集合作为算法结果,算法结束。
c) 基于频繁k项集,连接生成候选频繁k+1项集。
3) 令k=k+1,转入步骤2。
敲脑壳 重点来啦~
Apriori的算法的应用
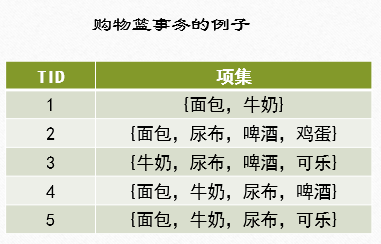
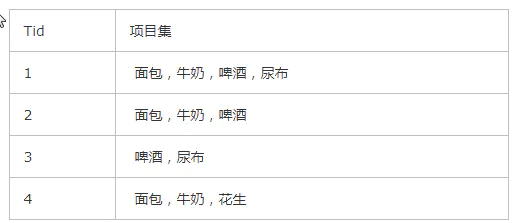
下面这个表格是代表一个事务数据库D,
其中最小支持度为50%,最小置信度为70%,求事务数据库中的频繁关联规则。
apriori算法的步骤如下所示:
(1)生成候选频繁1-项目集C1={{面包},{牛奶},{啤酒},{花生},{尿布}}。
(2)扫描事务数据库D,计算C1中每个项目集在D中的支持度。从事务数据库D中可以得出每个项目集的支持数分别为3,3,3,1,2,事务数据库D的项目集总数为4,因此可得出C1中每个项目集的支持度分别为75%,75%,75%,25%,50%。根据最小支持度为50%,可以得出频繁1-项目集L1={{面包},{牛奶},{啤酒},{尿布}}。
(3)根据L1生成候选频繁2-项目集C2={{面包,牛奶},{面包,啤酒},{面包,尿布},{牛奶,啤酒},{牛奶,尿布},{啤酒,尿布}}。
(4)扫描事务数据库D,计算C2中每个项目集在D中的支持度。从事务数据库D中可以得出每个项目集的支持数分别为3,2,1,2,1,2,事务数据库D的项目集总数为4,因此可得出C2中每个项目集的支持度分别为75%,50%,25%,50%,25%,50%。根据最小支持度为50%,可以得出频繁2-项目集L2={{面包,牛奶},{面包,啤酒},{牛奶,啤酒},{啤酒,尿布}}。
(5)根据L2生成候选频繁3-项目集C3={{面包,牛奶,啤酒},{面包,牛奶,尿布},{面包,啤酒,尿布},{牛奶,啤酒,尿布}},由于C3中项目集{面包,牛奶,尿布}中的一个子集{牛奶,尿布}是L2中不存在的,因此可以去除。同理项目集{面包,啤酒,尿布}、{牛奶,啤酒,尿布}也可去除。因此C3={面包,牛奶,啤酒}。
补充:到这边 这边已经是频繁最大项了 所以在这里面就可以计算他们的置信度
(6)扫描事务数据库D,计算C3中每个项目集在D中的支持度。从事务数据库D中可以得出每个项目集的支持数分别为2,事务数据库D的项目集总数为4,因此可得出C2中每个项目集的支持度分别为50%。根据最小支持度为50%,可以得出频繁3-项目集L3={{面包,牛奶,啤酒}}。
(7)L=L1UL2UL3={{面包},{牛奶},{啤酒},{尿布},{面包,牛奶},{面包,啤酒},{牛奶,啤酒},{啤酒,尿布},{面包,牛奶,啤酒}}。
(8)我们只考虑项目集长度大于1的项目集,例如{面包,牛奶,啤酒},它的所有非真子集{面包},{牛奶},{啤酒},{面包,牛奶},{面包,啤酒},{牛奶,啤酒},分别计算关联规则{面包}—>{牛奶,啤酒},{牛奶}—>{面包,啤酒},{啤酒}—>{面包,牛奶},{面包,牛奶}—>{啤酒},{面包,啤酒}—>{牛奶},{牛奶,啤酒}—>{面包}的置信度,其值分别为67%,67%,67%,67%,100%,100%。由于最小置信度为70%,可得},{面包,啤酒}—>{牛奶},{牛奶,啤酒}—>{面包}为频繁关联规则。也就是说买面包和啤酒的同时肯定会买牛奶,买牛奶和啤酒的同时也是会买面包。
由这个例子可以看出apriori主要是根据 最小支持度来判断的 逐步递进
but~这其中也有一些缺点: 从算法的步骤可以看出,Aprior算法每轮迭代都要扫描数据集,因此在数据集很大,数据种类很多的时候,算法效率很低。
以及图示栗子
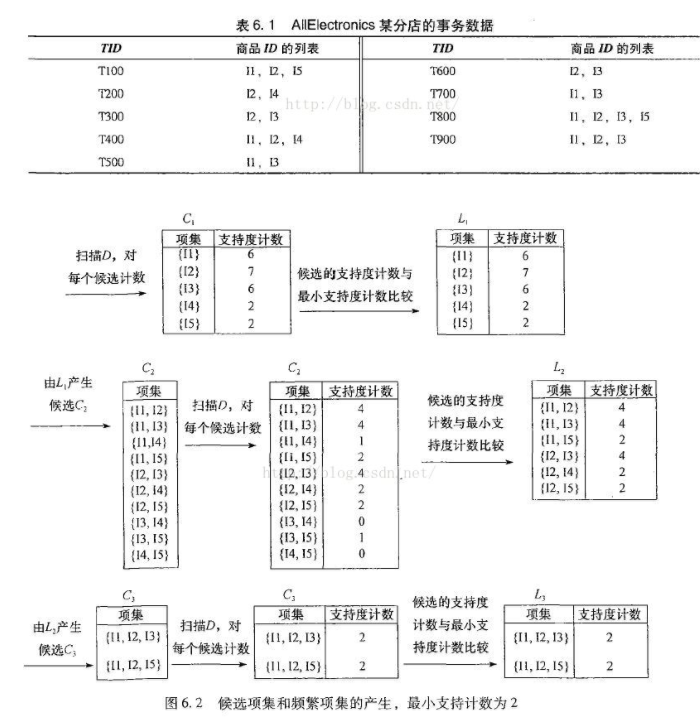
附相关解释图:

转载来自:链接:https://www.jianshu.com/p/26d61b83492e
呃呃呃背了两节课单词 突然课堂交作业。。。不到10分钟学完Apriori算法 别说了我和我朋友真牛逼需要补充的就是
计算置信度的话。。。。比如 啤酒牛奶->面包 分子是面包出现的次数 /(啤酒牛奶同时出现)的次数 这边没有搞清楚。。
补充
以及基于散列的方法优化


第一图是通过hash函数(10x+y) % 7 得到的~~~ 所以对于每一个TID 知道里面的项,可以两两配对之后算
我刚开始不是很明白 后来模拟了一下 比如TID = 1里面有I1,I2,I5 那么可以设x = 1,y = 2 或者x = 1 ,y = 5 或者 x = 2,y = 5 通过散列函数计算得到之后就扔进桶里面 OVER
我是这么理解的啦
原文出处:https://www.cnblogs.com/Galesaur-wcy/p/10541615.html