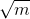功能

最快、最合适地判断一个数为素数

说明

分为打表法和单个判断法两类方法

打表法 是开始时将所有素数标记出来，适合多次调用判断，前两种属于打表法

单个判断法 则是只一个数一个数判断，适合少量判断来节省时间，后俩种属于单个判断法

四种方法：

方法一：素数筛（埃氏筛）（n<10^7）

方法二：欧拉筛（n<10^7）

方法三：遍历法（n<10^9）

方法四：Miller-Rabin算法（n<10^18)

方法一：素数筛（埃氏筛）（n<10^7）

N只需等于MAX的一半（因为j从i*i开始），这个算最常用的

#define MAX 10000005
#define N 4000
int vis[MAX]={1,1};
void Prime(){for(int i=2;i<= N;i++){if(!vis[i]){for(int j=i*i;j<=MAX;j+=i)vis[j]=1;      //0为素数}}
}

方法二：欧拉筛（n<10^7）

据说时间上接近O（n），实际上没有试过，空间复杂度基本一样

但欧拉筛的过程可以得到其最小的素数因子，有的题要使用改进后的欧拉筛

const long long MAX=10000005;
int prime[MAX];
int vis[MAX]={1,1};
void Prime(){for (int i = 2;i <= MAX; i++) {if (!vis[i])prime[++prime[0]] = i;for (int j = 1; j <=prime[0] && i*prime[j] <=MAX; j++) {vis[i*prime[j]] = 1;       //1为素数if (i % prime[j] == 0)break;}}
}

方法三：遍历法（n<10^9）

最经典的方法，优化后，只需判断从2到 $\sqrt{n}$ 即可

虽然复杂度较大，但对于单个判断还是很适用的。范围判断也可以判断1-1e6的所有次数，一般是用的最多的

bool fin(int x)
{if(x==1) return false;for(int i=2;i*i<=x;i++)if(x%i==0) return false;return true;     //1为素数
}

方法四：Miller-Rabin算法（n<10^18)

大概率地判断是否为素数详情见博客：Miller-Rabin算法

#include<algorithm>
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
#define ll long long
int prime[10]={2,3,5,7,11,13,17,19,23,29};
ll mul(ll a,ll b,ll c)     //快速积
{ll ans=0,res=a;while(b){if(b&1)ans=(ans+res)%c;res=(res+res)%c;b>>=1;}return (ll)ans;
}
ll qpow(ll a,ll b,ll c)     //快速幂
{ll ans=1,res=a;while(b){if(b&1)ans=mul(ans,res,c);res=mul(res,res,c);b>>=1;}return ans;
}
ll pri(ll x)     //判断素数，1为素数
{ll i,j,k;ll s=0,t=x-1;if(x==2)  return 1;if(x<2||!(x&1))  return 0;while(!(t&1)){s++;t>>=1;}for(i=0;i<10&&prime[i]<x;++i){ll a=prime[i];ll b=qpow(a,t,x);for(j=1;j<=s;++j){k=mul(b,b,x);if(k==1&&b!=1&&b!=x-1)return 0;b=k;}if(b!=1)  return 0;}return 1;
}