【数电】74161的同步与异步级联

article/2025/10/8 12:53:39

首先先提一下上一篇 7474触发器异步三进制加法计数器，在最后我写到一个小经验：如果用的是时钟的上升沿触发，异步连接时都是上级的Q反接下一级的时钟

后面我在复习数电考试的时候才发现原来老师之前就给做过笔记，如下：
在这里插入图片描述

正文：

异步与同步

置数与清除的同步与异步

这里的同步与异步主要是指计数器本身在置数与清除时会不会存在暂态
异步是存在暂态；同步是不存在暂态。
存在暂态的意思是最后一个状态是暂时的，一瞬间的，不会出现在循环中。

74160计数器是模10、8421BCD码、加法、同步置数、异步清除计数器；
74161计数器是模16、二进制、加法、同步置数、异步清除计数器；
74163计数器是模16、二进制、加法、同步置数、同步清除计数器；
故三种计数器在使用清除法时，74163计数器不需要考虑暂态，其它两种需要考虑。
而使用置数法时，三种计数器都不需考虑暂态。
（这里考不考虑暂态的意思就是…呃…后面根据具体例子说）

级联的同步与异步

这里的同步与异步就是指两个（也可以多个）计数器连起来时有两种连接方法：同步级联 与 异步级联。
这其实和之前的7474触发器同步与异步是一样的。
规律：同步级联用的是清零法；异步级联用的是置数法。
栗子：74161 计数器设计模36计数器。
同步级联：
在这里插入图片描述
注：这里的四输入与非门其实用二输入就行，因为我之前验证了其它模值的所以用到四个输入
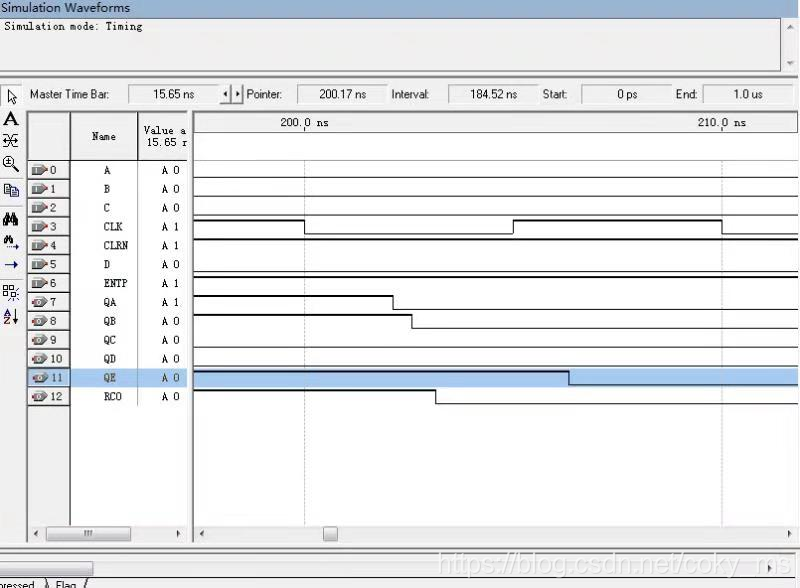
仿真结果：

从仿真结果可以看出它是从0（二进制：0000 0000）计数到35（二进制：0010 0011）
这里就可以来说说这个暂态的问题
目标是设计一个模36的计数器也就是一共36个状态。而且 74161 是异步清除也就是有暂态，那我在36的时候产生一个清除信号，因为最后一个36是暂态也就不会出现在循环状态里，仿真结果可以验证，35的下一个状态就回到初始状态。如果这里是同步清除，没有暂态，那按照这种接法，36就会出现在循环状态中，0到36一共就37个状态，就不满足设计要求。所以应该把产生清除信号的状态往前移一个，也就是在35的时候就产生。
异步级联：
在这里插入图片描述
仿真结果：

从仿真结果可以看出异步级联并不是按顺序 0-35，因为我设计的是 4x9 所以低位片每产生4个信号时会给高位片产生一个时钟信号。高位片一共9个状态，每个状态都是低位片的4个状态，这种组合就有36个状态。