1.贝叶斯估计的思想

在统计学中有两大学派：频率学派和贝叶斯学派。针对参数估计的方法也分成两派。其中以极大似然估计为代表的频率学派和以贝叶斯估计为代表的贝叶斯学派。
本文将详细介绍贝叶斯估计的细节。贝叶斯用概率反映知识状态的确定性程度。其基本观点是：对于任意未知量 $\theta$ ，由于真实参数 $\theta$ 是未知或不确定的，因此可以表示成随机变量，可以用一个概率分布去描述，这个分布称为先验分布。 在获得样本后，总体分布、样本与先验分布通过贝叶斯公式结合得到了一个关于参数 $\theta$ 的新的分布——后验分布。
根据以上思想，可以根据贝叶斯公式给出贝叶斯估计的形式。
设样本 $X=({x_{1},x_{2},...,x_{m}})$ 来自总体 $p(X|\theta)$ , $\theta\in\Theta$ ,参数 $\theta$ 的先验信息通过先验分布 $\pi (\theta)$ 确定。此时样本 $X=({x_{1},x_{2},...,x_{m}})$ 的联合条件概率函数为：
$p(X|\theta)=p(x_{1},x_{2},...,x_{m}|\theta)=\prod_{i=1}^{m} p(x_{i},\pmb{\theta }) \tag{1.1}$
根据条件概率公式，样本 $X$ 和参数 $\theta$ 的联合概率为
$h(X,\theta)=p(X|\theta)\pi (\theta) \tag{1.2}$
在获得上述联合概率之后，可以得到后验概率
$p(\theta|X)=\frac{h(X,\theta)}{p_{m}{(X)}}=\frac{p(X|\theta)\pi (\theta)}{p_{m}(X)} \tag{1.3}$
其中 $p_{m}(X)$ 是 $X$ 的边际概率，由以下式子确定
$p_{m}(X)=\int_{\Theta }h(X,\theta)d\theta=\int_{\Theta }p(X|\theta)\pi (\theta)d\theta \tag{1.4}$
根据式(1.3)(1.4)得后验分布：
$p(\theta|X)=\frac{p(X|\theta)\pi (\theta)}{\int_{\Theta }p(X|\theta)\pi (\theta)d\theta} \tag{1.5}$
由后验分布 $p(\theta|X)$ 估计参数 $\theta$ 主要有以下三种方法：

最大后验估计——使用后验分布的密度函数最大值点作为 $\theta$ 的点估计.
后验中位数估计——使用后验分布的中位数作为 $\theta$ 的点估计.
后验期望估计——使用后验分布的均值作为 $\theta$ 的点估计.

2.正态总体参数贝叶斯估计的推导

设样本 $X=({x_{1},x_{2},...,x_{m}})$ 是来自正态分布 $N(\mu,\sigma_{0}^{2})$ 的一个样本，其中 $\sigma_{0}^{2}$ 已知， $\mu$ 未知，假设 $\mu$ 的先验分布也为正态分布 $N(\theta,\tau^{2})$ ，其中先验均值 $\theta$ 和先验方差 $\tau^{2}$ 均为已知。
根据贝叶斯估计的过程，可得
$\begin{aligned} p(X|\mu)&=\prod_{i=1}^{m} p(x_{i},\mu ) \\ &=\prod_{i=1}^{m} \frac{1}{\sqrt{2\pi}\sigma_{0}}exp\{-\tfrac{(x_{i}-\mu )^{2}}{2\sigma_{0}^{2}}\} \\ &=(2\pi\sigma_{0}^{2})^{-m/2}exp\{-\frac{1}{2\sigma_{0}^{2}}\sum_{i=1}^{m}(x_{i}-\mu )^{2}\} \tag{2.1} \end{aligned}$
以及
$\begin{aligned} \pi(\mu)=\frac{1}{\sqrt{2\pi}\tau}exp\{-\frac{(\mu-\theta )^{2}}{2\tau^{2}}\} \tag{2.2} \end{aligned}$
由公式(2.1)和(2.2)可得样本 $X$ 和参数 $\mu$ 的联合概率

$\begin{aligned} h(X,\mu)&=p(X|\mu)\pi (\mu)\\ &=(2\pi\sigma_{0}^{2})^{-m/2}\frac{1}{\sqrt{2\pi}\tau}exp\{-\frac{1}{2\sigma_{0}^{2}}\sum_{i=1}^{m}(x_{i}-\mu )^{2}\}exp\{-\frac{(\mu-\theta )^{2}}{2\tau^{2}}\} \\ &=c\cdot exp\{ -\frac{m\mu^{2}-2m\mu\bar{x}+\sum_{i=1}^{m}x_{i}^{2}}{2\sigma_{0}^{2}}-\frac{\mu^{2}-2\theta\mu+\theta^{2}}{2\tau^{2}} \}\\ &=c\cdot exp\{-\frac{1}{2}[\frac{m\mu^{2}-2m\mu\bar{x}+\sum_{i=1}^{m}x_{i}^{2}}{\sigma_{0}^{2}}+\frac{\mu^{2}-2\theta\mu+\theta^{2}}{\tau^{2}} ]\}\tag{2.3} \end{aligned}$
其中 $\bar{x}=\frac{1}{m}\sum_{i=1}^{m}x_{i},c=(2\pi)^{-(m+1)/2}\tau^{-1}\sigma_{0}^{-m}$
记
$A=\frac{m}{\sigma_{0}^{2}}+\frac{1}{\tau^{2}},B=\frac{m\bar{x}}{\sigma_{0}^{2}}+\frac{\theta}{\tau^{2}},C=\frac{\sum_{i=1}^{m}x_{i}^{2}}{\sigma_{0}^{2}}+\frac{\theta^{2}}{\tau^{2}} \tag{2.4}$
则有
$\begin{aligned} h(X,\mu) &=c\cdot exp\{-\frac{1}{2}[A\mu^{2}-2B\mu+C]\}\\ &=c\cdot exp\{-\frac{(\mu-B/A)^{2}}{2/A}-\frac{C-B^{2}/A}{2}\}\tag{2.5} \end{aligned}$
考虑到 $A, B, C$ 均与 $\mu$ 无关，故容易计算 $X$ 的边际概率密度函数为
$\begin{aligned} p_{m}(X)&= \int_{-\infty}^{+\infty}h(X,\mu)d\mu\\ &=c\cdot (2\pi/A)^{1/2}exp\{-\frac{C-B^{2}/A}{2}\}\\\tag{2.6} \end{aligned}$
应用贝叶斯公式可得
$\begin{aligned} p(\mu|X)&= \frac{h(X,\mu)}{p_{m}{(X)}}\\ &=(2\pi/A)^{-1/2}exp\{-\frac{(\mu-B/A)^{2}}{2/A}\}\\ \tag {2.7} &=\frac{1}{\sqrt{2\pi}A^{-1/2}}exp\{-\frac{(\mu-B/A)^{2}}{2A^{-1}}\} \end{aligned}$
从上式可知， $\mu$ 的后验分布为 $N (B / A, 1/ A)$ ，即
$\mu|X\sim N(\frac{m\bar{x}\sigma_{0}^{-2}+\theta\tau^{-2}}{m\sigma_{0}^{-2}+\tau^{-2}},\frac{1}{m\sigma_{0}^{-2}+\tau^{-2}}) \tag {2.8}$
后验分布的均值即为参数 $\mu$ 的后验期望估计
$\hat{\mu}=\frac{m\bar{x}\sigma_{0}^{-2}+\theta\tau^{-2}}{m\sigma_{0}^{-2}+\tau^{-2}} \tag {2.9}$

3.代码实现

3.1.抽取样本

import numpy as np
import matplotlib.pyplot as plt

首先从 $\mu=2,\sigma=4$ 的正态分布中抽取 $m = 100000$ 个样本

np.random.seed(10)
mu=2;sigma=4;m=100000
X=np.sort(np.random.normal(mu,sigma,m))
y=(1/np.sqrt(2*np.pi)*sigma)*np.exp(-(X-mu)**2/(2*sigma**2))

3.2.估计参数

根据后验分布，使用python实现 $\hat{\mu}$ ，即式(2.9)

def bayesian_estimate(X,sigma0,theta,tau):m=len(X)mu_p=(m*np.mean(X)*(sigma0**-2)+theta*(tau**-2))/(m*(sigma0**-2)+(tau**-2))sigma_p=(1)/(m*(sigma0**-2)+(tau**-2))return mu_p,np.sqrt(sigma_p)

假设 $\mu$ 的先验分布为 $N (4, 4)$ ，得到后验均值估计：

mu_p,sigma_p=bayesian_estimate(X,sigma,4,2)
print("后验分布均值：:{}\n后验分布标准差:{}".format(mu_p,sigma_p))

结果：

后验分布均值：:1.9881668135649222

后验分布标准差:0.012648857666049918

对应的最大后验估计和后验中位数估计为

mu_p_median=np.median(X1)
mu_p_max=X1[np.argmax(y1)]
print("后验中位数估计：{}\n最大后验估计：{}".format(mu_p_median,mu_p_max))

结果：

后验中位数估计：1.9881840597010452

最大后验估计：1.988166738777464

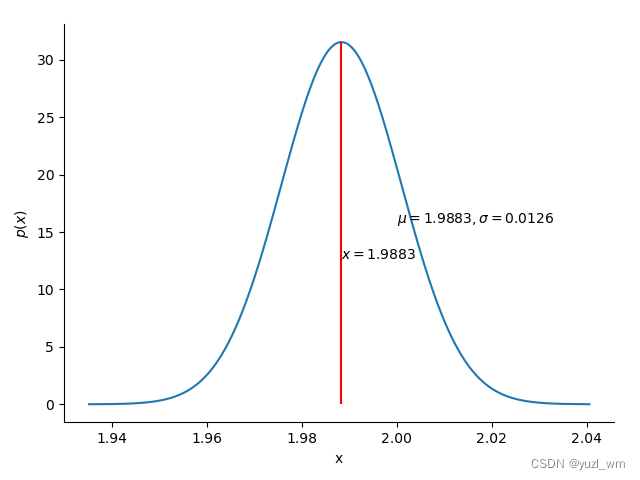
def plot_density(X,y,mu,sigma):fig=plt.Figure()grid=plt.GridSpec(1,1)axes=fig.add_subplot(grid[0,0])axes.plot(X,y)axes.set_xlabel("x")axes.set_ylabel("$p(x)$")for dire in ['top','right']:axes.spines[dire].set_visible(False)axes.vlines(mu,ymin=0,ymax=np.max(y),color='red')axes.text(2, 0.5*np.max(y), '$\mu={},\sigma={}$'.format(round(mu,4),round(sigma,4)))fig.subplots_adjust(left=0.1, bottom=0.12, right=0.96, top=0.95, wspace=0.5, hspace=0.5)axes.text(mu, 0.4*np.max(y), '$x={}$'.format(round(mu,4)))return fig

从后验分布中抽取100000个样本，绘制后验分布概率密度曲线，如下图：

X1=np.sort(np.random.normal(mu_p,sigma_p,100000))
y1=(1/(np.sqrt(2*np.pi)*sigma_p))*np.exp(-(X1-mu_p)**2/(2*sigma_p**2))
fig=plot_density1(X1,y1,mu_p,sigma_p)

在这里插入图片描述

4.总结

从估计结果来看，贝叶斯估计对总体均值的估计误差较小。

参考文献

[1] 茆诗松,程依明,濮晓龙.概率论与数理统计教程[M]. 北京:高等教育出版社, 2019. 294-298.
[2] Rice J A. Mathematical statistics and data analysis[M]. Cengage Learning, 2006.
[3] Goodfellow I, Bengio Y, Courville A. Deep learning[M]. MIT press, 2016.