1、实验内容

由于生活中很多参数如测量误差、产品质量指标等几乎都服从或近似服从正态分布，所以可以用对单变量正态分布中的贝叶斯估计进行分析并编写相应的Matlab程序，分析样本大小对贝叶斯估计误差的影响，进而验证贝叶斯估计的有效性。

2、实验原理

1、了解贝叶斯估计原理，以单变量正态分布为例，设X^N={X₁,X₂,…,X_N}z是取自正态分布N(μ，σ²)的样本集。假设其中的总体方差σ²已知：μ是未知的随机参数，为带估计量，且已有先验分布N(μ₀，σ²₀)，要求使用贝叶斯估计方法求出估计量μ^，使得最终的贝叶斯风险最小。
2、利用Matlab中得函数生成一定数量得总体分布密度服从正态分布得样本数据。
3、由单变量正态分布得到的贝叶斯估计值计算公式：μ^ = N*σ²mN/(Nσ²₀+σ²)+σ²μ₀/(Nσ²₀+σ²)
4、以上叙述生成的样本为基础，继续添加服从同样的正态分布的样本数据集，探索贝叶斯估计值和样本大小的关系。

实验方法集程序

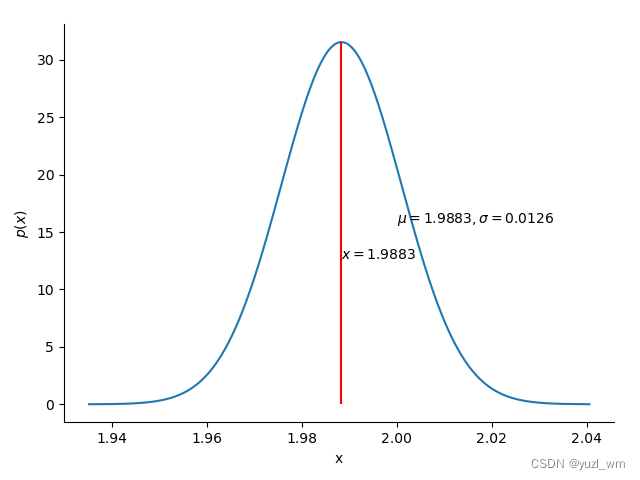
1、假定p(μ) ~ N(2.8,0.6²)，展示数据

>> u = 2.4;%总体分布概率的均值
>> sigma = 3.6;%总体分布概率的标准差
>> #假设某一样本：
>> u0 = 2.8;%未知参数分布的均值
>> sigma0 = 0.6;%未知参数分布的标准差
>> num=200;%样本个数
>> XN = normrnd(u,sigma,1,num);
>> mN = sun(XN)/num;%样本均值

未知参数的分布：

2、利用贝叶斯估计对其进行估计：

>> 贝叶斯估计值
>> u1 = num*sigma0^2*mN/(num*sigma0^2+sigma^2)+sigma^2*u0/(num*sigma0^2+sigma^2);
>> 计算相对误差
>> abs(u1-u)/u*100
>ans =19.25

u1的值：

3、以上述200个数据为基础，继续添加服从正态分布N(2.8,0.6²)的样本数据，探索贝叶斯估计值和样本大小的关系：

for num =1:3000u = 2.4;%总体分布概率的均值sigma = 3.6;%总体分布概率的标准差R = normrnd(u,sigma,1,1);%产生一个和前面样本分布一样的样本数据sigma0 = 0.6;%未知参数分布的标准差u0 = 2.8;%未知参数分布的均值XN = [XN,R];%XN的前200个值为上个程序已经产生的样本数据mN = sum(XN)/(num+100);u1(num)=(num+100)*sigma0^2*mN/((num+100)*sigma0^2+sigma^2+sigma^2*u0/((num+100)*sigma0^2+sigma^2));%画出相对误差plot(abs(u1-u)/u);xlabel("增大样本数");ylabel('相对误差')grid on;hold on;
end
>> plot(u1);
>> xlabel("增大样本数");
>> ylabel('贝叶斯估计值');

实验结果与分析

1、实验一：可以看出贝叶斯的估计值为19.25％，与真实值的误差值较大，这是由于样本数量较少，导致先验信息不够，最终估计值与真实值存在较大的误差。
2、实验二：可以看出，贝叶斯估计值在样本数较少时距离真实值较远，误差较大，随着样本数的增加首先呈现下降趋势，然后慢慢的平稳下来靠近真实值。说明贝叶斯估计值的误差大小与样本数有关系，当样本数足够大时，贝叶斯估计和被估计的真实值之间的误差将控制在合理的范围。