知乎上有个专题叫：你对贝叶斯统计有怎样的理解？本篇尽量通俗点理解下贝叶斯统计~_~

还是沿用经典案例：

一种癌症，得了这个癌症的人被检测出为阳性的几率为90%，未得这种癌症的人被检测出阴性的几率为90%，而人群中得这种癌症的几率为1%，一个人被检测出阳性，问这个人得癌症的几率为多少？

似然函数与最大似然估计：

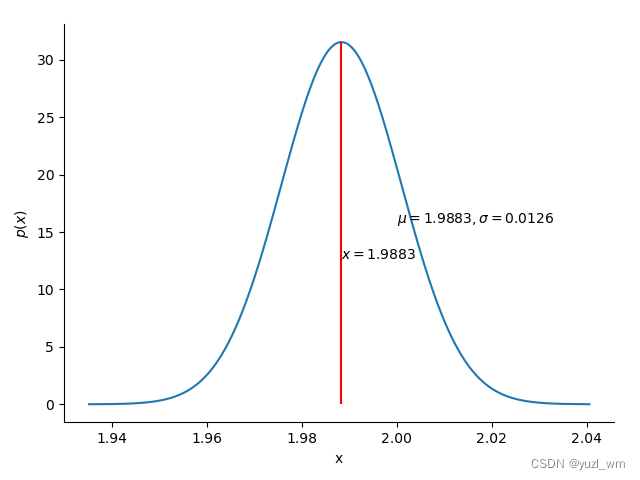
上面公式中的 f(x|θ) 就是一种似然函数，观测到样本x 的分布是在以某个参数θ为前提下得出来的，只是这个参数是未知的，在统计学里常用的求该参数的方法就是：最大似然估计了。

假设我们有个样本 , 它们每一个变量都对应一个似然函数:

把这些似然函数乘起来:

只要找到令这个函数最大的 θ 值，就是我们想要的参数值了。

朴素贝叶斯：

对于给出的待分类项，求出在此分类项出现的情况下各个类别出现的概率，哪个最大，就认为待分类项属于哪个类别。即在没有其它可用的信息时，选择条件概率最大的类别。朴素贝叶斯分类的定义如下：

      1、设为待分类项，ai 为x的一个特征属性。

      2、类别集合 。

      3、计算 。

      4、去最大概率值 ，则 。

     关键一步在于如何计算第3步中的条件概率。通常采用的做法是：

      1、找到一个已知分类的待分类项集合，作为训练样本集。

      2、统计在各个类别下各特征属性的条件概率估计：

           。

      3、如果各个特征属性是条件独立的，即符合马尔科夫模型，则贝叶斯定理成立：

          

      P(x)对于所有类别都是一个常数，所以取极值就变为将分子最大化：        

朴素贝叶斯分类的流程：

（1）准备工作阶段。主要是根据具体情况确定特征属性，并对特征属性进行划分，由人工对一部分待分类项进行分类，形成训练样本集合。这一阶段的输入是待分类数据，输出是特征属性和训练样本。这一阶段需要人工完成的，对整个过程有重要影响，分类器的质量很大程度上由特征属性、特征属性划分及训练样本的质量决定。

（2）分类器训练阶段。主要是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率估计，并将结果记录。其输入是特征属性和训练样本，输出是分类器。

（3）应用阶段。使用分类器对待分类项进行分类，输入分类器和待分类项，输出待分类项与类别的映射关系。

注：当P(a|y)=0，即某个类别下某个特征项划分没有出现，这会令分类器质量大大降低。为了解决这个问题，通常对没类别下所有划分的计数加1，这样如果训练样本集数量充分大时，并不会对结果产生影响，并且解决了上述频率为0的尴尬局面。