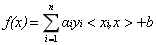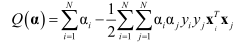1.概念

支持向量机（Support Vector Machine, SVM）是一类按监督学习（supervised learning）方式对数据进行二元分类的广义线性分类器（generalized linear classifier），其决策边界是对学习样本求解的最大边距超平面.它分类的思想是，给定给一个包含正例和反例的样本集合，svm的目的是寻找一个超平面来对样本根据正例和反例进行分割，从而达到分类的目的。

2.SVM-线性分类器

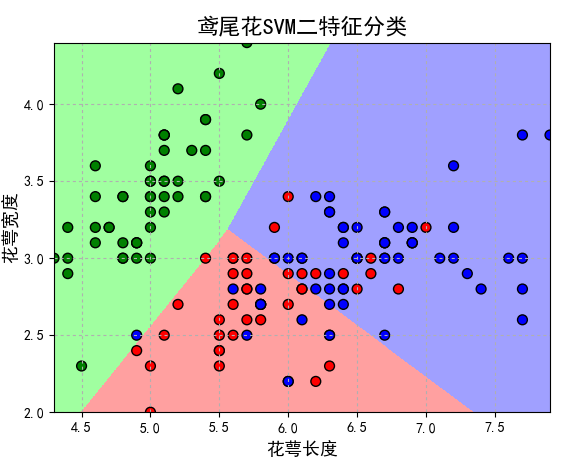
 对于二维空间来说，我理解的是能够在给定两组不同的数据中用一条直线把这两组数据给分离开来，如下图示。

 

 超平面

对于多维来说，如果能够存在一个线性函数能够将样本完全正确的分离开来，那么这些数据就是线性可分的，反之，称为非线性可分的。什么叫线性函数呢？通俗地讲，就是在一维空间里就是一个点，在二维空间里就是一条直线，三维空间里就是一个平面，以此类推。
如果不关注空间的维数，这种线性函数其实就是超平面。

下面讲述一个例子（转自视频：https://www.bilibili.com/video/BV1D64y1f7r6?p=1）：

 在样本空间中，我们可以用线性方程来说明：

 对于二维空间来说，线性方程可表示为：w1x1+w2x2+b=0。其中，w=(w1;w2;w3;……w d)为法向量，决定超平面的方向；b为位移项，决定了超平面与原点之间的距离，显然,划分超平面可被法向量w和位移b确定，下面我们将其记为(w，b)。样本空间中任意点x到超平面(w，b)的距离可写为

                        

 

在分类问题中给定输入数据和学习目标：

 ，其中输入数据的每个样本都包含多个特征并由此构成特征空间（feature space）：

，而学习目标为二元变量表示负类（negative class）和正类（positive class）。

若输入数据所在的特征空间存在作为决策边界（decision boundary）的超平面将学习目标按正类和负类分开，并使任意样本的点到平面距离大于等于1 [2]  ：

则称该分类问题具有线性可分性，参数w,b分别为超平面的法向量和截距。

满足该条件的决策边界实际上构造了2个平行的超平面作为间隔边界以判别样本的分类：

 

所有在上间隔边界上方的样本属于正类，在下间隔边界下方的样本属于负类。两个间隔边界的距离

被定义为边距（margin），位于间隔边界上的正类和负类样本为支持向量（support vector）。

 

 拉格朗日乘子法求得KNN条件：

SM算法

非线性分类：把数据放到高维度上再次进行分割

 

 

 

 当f(x)=x时，这组数据是个直线，如上半部分，但是当我把这组数据变为f(x)=x^2时，这组数据就变成了下半部分的样子，也就可以被红线所分割

 核函数：

SVM通过某非线性变换 φ( x) ，将输入空间映射到高维特征空间。特征空间的维数可能非常高。如果SVM的求解只用到内积运算，而在低维输入空间又存在某个函数 K(x, x′) ，它恰好等于在高维空间中这个内积，即K( x, x′) =<φ( x) ⋅φ( x′) > 。那么支持向量机就不用计算复杂的非线性变换，而由这个函数 K(x, x′) 直接得到非线性变换的内积，使大大简化了计算。这样的函数 K(x, x′) 称为核函数。

             常见核函数：

                h度多项式核函数

                高斯径向基和函数：图像分类

                S型核函数

 

 在机器学习领域，支持向量机SVM(Support Vector Machine)是一个有监督的学习模型，通常用来进行模式识别、分类(异常值检测)以及回归分析。

   其具有以下特征：

   (1)SVM可以表示为凸优化问题，因此可以利用已知的有效算法发现目标函数的全局最小值。而其他分类方法都采用一种基于贪心学习的策略来搜索假设空间，这种方法一般只能获得局部最优解。

  (2) SVM通过最大化决策边界的边缘来实现控制模型的能力。尽管如此，用户必须提供其他参数，如使用核函数类型和引入松弛变量等。

  (3)SVM一般只能用在二类问题，对于多类问题效果不好。

from sklearn import svm
import numpy as np
import matplotlib.pyplot as plt#准备训练样本
x=[[1,8],[3,20],[1,15],[3,35],[5,35],[4,40],[7,80],[6,49]]
y=[1,1,-1,-1,1,-1,-1,1]##开始训练
clf=svm.SVC()  ##默认参数：kernel='rbf'
clf.fit(x,y)#print("预测...")
#res=clf.predict([[2,2]])  ##两个方括号表面传入的参数是矩阵而不是list##根据训练出的模型绘制样本点
for i in x:res=clf.predict(np.array(i).reshape(1, -1))if res > 0:plt.scatter(i[0],i[1],c='r',marker='*')else :plt.scatter(i[0],i[1],c='g',marker='*')##生成随机实验数据(15行2列)
rdm_arr=np.random.randint(1, 15, size=(15,2))
##回执实验数据点
for i in rdm_arr:res=clf.predict(np.array(i).reshape(1, -1))if res > 0:plt.scatter(i[0],i[1],c='r',marker='.')else :plt.scatter(i[0],i[1],c='g',marker='.')
##显示绘图结果
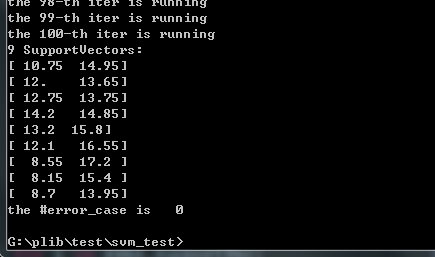
plt.show()

 运行结果：

 

 

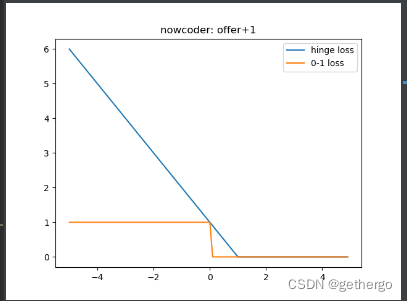
松弛变量：

数据本身可能有噪点，会使得原本线性可分的数据需要映射到高维度去。对于这种偏离正常位置很远的数据点，我们称之为 outlier ，在我们原来的 SVM 模型里，outlier 的存在有可能造成很大的影响，因为超平面本身就是只有少数几个 support vector 组成的，如果这些 support vector 里又存在 outlier 的话，其影响就很大了。

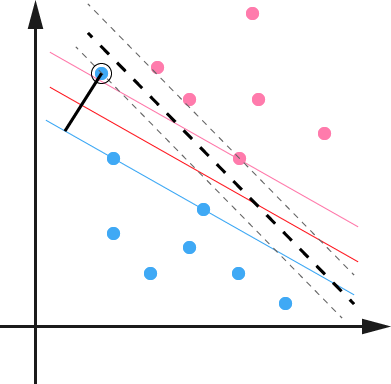
因此排除outlier点，可以相应的提高模型准确率和避免Overfitting的方式。

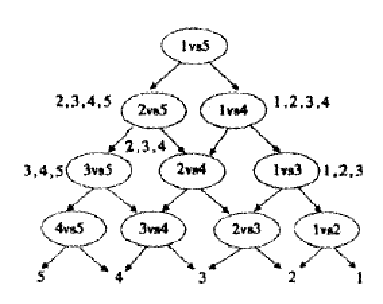
解决多分类问题：

经典的SVM只给出了二类分类的算法，现实中数据可能需要解决多类的分类问题。因此可以多次运行SVM，产生多个超平面，如需要分类1-10种产品，首先找到1和2-10的超平面，再寻找2和1,3-10的超平面，以此类推，最后需要测试数据时，按照相应的距离或者分布判定。

SVM与其他机器学习算法对比(图)：

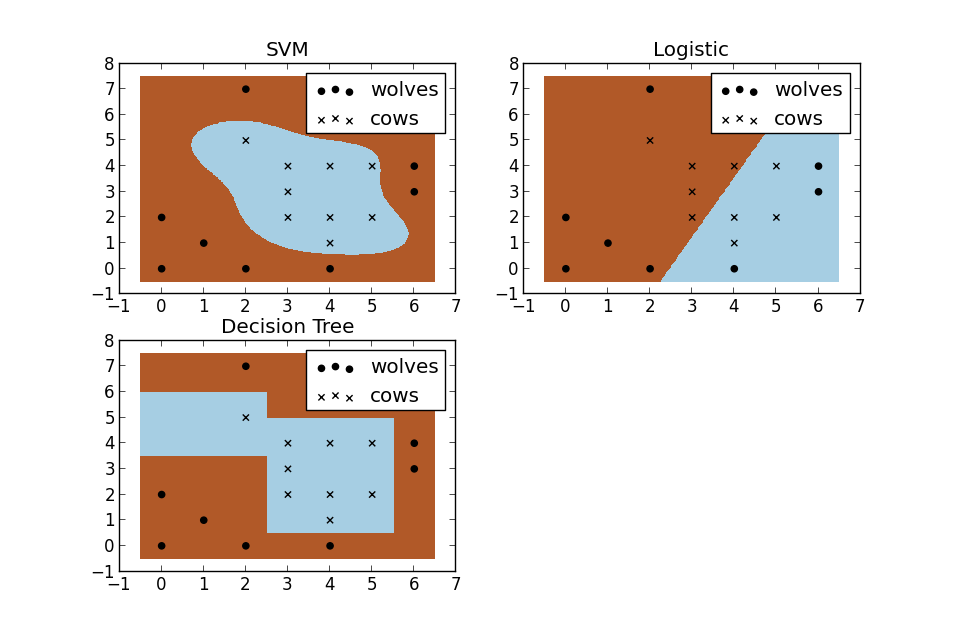
代码如下：

from sklearn import svm
import numpy as np
import matplotlib.pyplot as plt##设置子图数量
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(7, 7))
ax0, ax1, ax2, ax3 = axes.flatten()# 准备训练样本
x = [[1, 8], [3, 20], [1, 15], [3, 35], [5, 35], [4, 40], [7, 80], [6, 49]]
y = [1, 1, -1, -1, 1, -1, -1, 1]
'''说明1：核函数(这里简单介绍了sklearn中svm的四个核函数，还有precomputed及自定义的)LinearSVC：主要用于线性可分的情形。参数少，速度快，对于一般数据，分类效果已经很理想RBF:主要用于线性不可分的情形。参数多，分类结果非常依赖于参数polynomial:多项式函数,degree 表示多项式的程度-----支持非线性分类Sigmoid：在生物学中常见的S型的函数，也称为S型生长曲线说明2：根据设置的参数不同，得出的分类结果及显示结果也会不同'''
##设置子图的标题
titles = ['LinearSVC (linear kernel)','SVC with polynomial (degree 3) kernel','SVC with RBF kernel',  ##这个是默认的'SVC with Sigmoid kernel']
##生成随机试验数据(15行2列)
rdm_arr = np.random.randint(1, 15, size=(15, 2))def drawPoint(ax, clf, tn):##绘制样本点for i in x:ax.set_title(titles[tn])res = clf.predict(np.array(i).reshape(1, -1))if res > 0:ax.scatter(i[0], i[1], c='r', marker='*')else:ax.scatter(i[0], i[1], c='g', marker='*')##绘制实验点for i in rdm_arr:res = clf.predict(np.array(i).reshape(1, -1))if res > 0:ax.scatter(i[0], i[1], c='r', marker='.')else:ax.scatter(i[0], i[1], c='g', marker='.')if __name__ == "__main__":##选择核函数for n in range(0, 4):if n == 0:clf = svm.SVC(kernel='linear').fit(x, y)drawPoint(ax0, clf, 0)elif n == 1:clf = svm.SVC(kernel='poly', degree=3).fit(x, y)drawPoint(ax1, clf, 1)elif n == 2:clf = svm.SVC(kernel='rbf').fit(x, y)drawPoint(ax2, clf, 2)else:clf = svm.SVC(kernel='sigmoid').fit(x, y)drawPoint(ax3, clf, 3)plt.show()

运行结果：