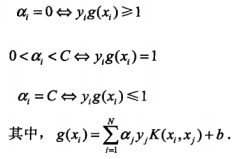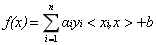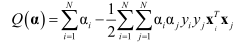零.
本文所有代码均能在我 github上的 DML 找到,顺便求点Star
一.引入
从一开始接触机器学习,就感觉SVM(支持向量机 Support Vector Machine)就是高端大气上档次的代名词啊,在深度学习出来之前一直都力压ANN一头,是应用得最好的算法了,本文借着实现DML的机会实现一下。
二.原理
SVM的文章先不说论文和书啦,博文也是不少,所以我觉得实在不用在这里赘述这些了,这是标题里原理打引号的原因……
现推荐这些博客里讲的SVM,我认为写得是极好的:
JerryLead 的五篇 很好理解
july的博客 ,还是那啥的风格,大长篇……事实上我没看完这个…只是觉得挺全的
除此之外还可以去看看《统计学习方法》的内容
三.过程.
接下来讲一下我选择实现的SOM的基本过程吧:
SMO是(Sequential minimal optimization),其优化过程就是每次选取两个优化变量α(i)和α(j),然后更新α,直到满足停机条件为止:
我基本上是按照《统计学习方法》来实现的,所以也就直接贴一下这上面的过程:

至于alpha的选择,第一个变量的选择是要选择违反KKT条件的:
代码的这里不是直接这样实现的,因为用了Ei,为了方便形式有所改变,但你可以推一下是没问题的:
第二个变量的选择是选择使|Ei-Ej|最大的,然后按照一定的规则计算和更新就行了
四.实现与测试
这是DML/SVM/svm.py
from __future__ import division
import numpy as np
import scipy as sp
from dml.tool import sign
import matplotlib.pyplot as plt
from numpy.random import random
import random as rd
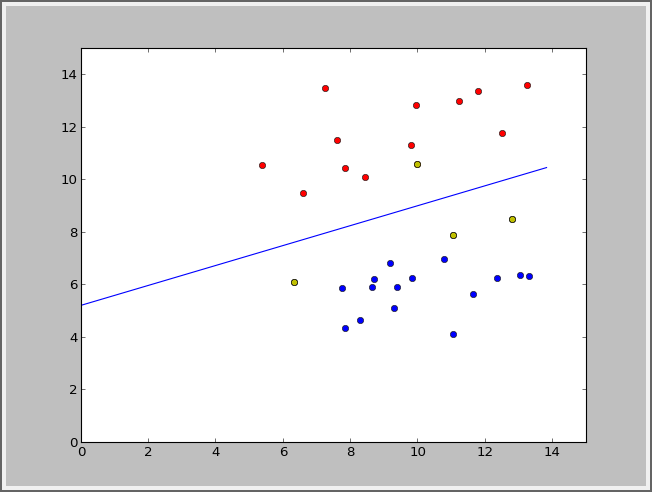
class SVMC:def Gauss_kernel(x,z,sigma=2):return np.exp(-np.sum((x-z)**2)/(2*sigma**2))def Linear_kernel(x,z):return np.sum(x*z)def __init__(self,X,y,C=10,tol=0.01,kernel=Linear_kernel):'''X is n N*M matrix where N is #features and M is #train_case'''self.X=np.array(X)self.y=np.array(y).flatten(1)self.tol=tolself.N,self.M=self.X.shapeself.C=Cself.kernel=kernelself.alpha=np.zeros((1,self.M)).flatten(1)self.supportVec=[]self.b=0self.E=np.zeros((1,self.M)).flatten(1)def fitKKT(self,i):if ((self.y[i]*self.E[i]<-self.tol) and (self.alpha[i]<self.C)) or \(((self.y[i]*self.E[i]>self.tol)) and (self.alpha[i]>0)):return Falsereturn True def select(self,i):pp=np.nonzero((self.alpha>0))[0]if (pp.size>0):j=self.findMax(i,pp)else:j=self.findMax(i,range(self.M))return jdef randJ(self,i):j=rd.sample(range(self.M),1)while j==i:j=rd.sample(range(self.M),1)return j[0]def findMax(self,i,ls):ansj=-1maxx=-1self.updateE(i)for j in ls:if i==j:continueself.updateE(j)deltaE=np.abs(self.E[i]-self.E[j])if deltaE>maxx:maxx=deltaEansj=jif ansj==-1:return self.randJ(i)return ansjdef InerLoop(self,i,threshold):j=self.select(i)#print i,j,self.y[i]==self.y[j],self.alpha[i],self.alpha[j],self.C#print self.y[i],self.y[j]self.updateE(j)self.updateE(i)if (self.y[i]==self.y[j]):L=max(0,self.alpha[i]+self.alpha[j]-self.C)H=min(self.C,self.alpha[i]+self.alpha[j])else:L=max(0,self.alpha[j]-self.alpha[i])H=min(self.C,self.C+self.alpha[j]-self.alpha[i])#print L,Ha2_old=self.alpha[j]a1_old=self.alpha[i]#print i,j#if L==H:# return TrueK11=self.kernel(self.X[:,i],self.X[:,i])K22=self.kernel(self.X[:,j],self.X[:,j])K12=self.kernel(self.X[:,i],self.X[:,j])eta=K11+K22-2*K12if eta==0:return Trueself.alpha[j]=self.alpha[j]+self.y[j]*(self.E[i]-self.E[j])/etaif self.alpha[j]>H:self.alpha[j]=Helif self.alpha[j]<L:self.alpha[j]=Lif np.abs(self.alpha[j]-a2_old)<threshold:#print np.abs(a2_new-self.alpha[j])return True#print np.abs(a2_new-self.alpha[j]),"improve"self.alpha[i]=self.alpha[i]+self.y[i]*self.y[j]*(a2_old-self.alpha[j])b1_new=self.b-self.E[i]-self.y[i]*K11*(self.alpha[i]-a1_old)-self.y[j]*K12*\(self.alpha[j]-a2_old)b2_new=self.b-self.E[j]-self.y[i]*K12*(self.alpha[i]-a1_old)-self.y[j]*K22*\(self.alpha[j]-a2_old)#print a1_new,"a1 new"#print a2_new,"a2 new"if self.alpha[i]>0 and self.alpha[i]<self.C:self.b=b1_newelif self.alpha[j]>0 and self.alpha[j]<self.C:self.b=b2_newelse: self.b=(b1_new+b2_new)/2#self.alpha[i]=a1_new#self.alpha[j]=a2_newself.updateE(j)self.updateE(i)return Falsepassdef updateE(self,i):#self.supportVec=np.nonzero((self.alpha>0))[0]self.E[i]=0for t in range(self.M):#for t in range(self.M):self.E[i]+=self.alpha[t]*self.y[t]*self.kernel(self.X[:,i],self.X[:,t])self.E[i]+=self.b-self.y[i]def train(self,maxiter=100,threshold=0.000001):iters=0flag=Falsefor i in range(self.M):self.updateE(i)while (iters<maxiter) and (not flag):flag=Truetemp_supportVec=np.nonzero((self.alpha>0))[0]iters+=1for i in temp_supportVec:self.updateE(i)if (not self.fitKKT(i)):flag=flag and self.InerLoop(i,threshold)#if not flag:breakif (flag):for i in range(self.M):self.updateE(i)if (not self.fitKKT(i)):flag= flag and self.InerLoop(i,threshold)#if not flag:break print "the %d-th iter is running" % itersself.supportVec=np.nonzero((self.alpha>0))[0]def predict(self,x):w=0for t in self.supportVec:w+=self.alpha[t]*self.y[t]*self.kernel(self.X[:,t],x).flatten(1)w+=self.breturn sign(w)def pred(self,X):test_X=np.array(X)y=[]for i in range(test_X.shape[1]):y.append(self.predict(test_X[:,i]))return ydef error(self,X,y):py=np.array(self.pred(np.array(X))).flatten(1)#print y,pyprint "the #error_case is ",np.sum(py!=np.array(y))def prints_test_linear(self):w=0for t in self.supportVec:w+=self.alpha[t]*self.y[t]*self.X[:,t].flatten(1)w=w.reshape(1,w.size)print np.sum(sign(np.dot(w,self.X)+self.b).flatten(1)!=self.y),"errrr"#print w,self.bx1=0y1=-self.b/w[0][1]y2=0x2=-self.b/w[0][0]plt.plot([x1+x1-x2,x2],[y1+y1-y2,y2])#plt.plot([x1+x1-x2,x2],[y1+y1-y2-1,y2-1])plt.axis([0,30,0,30])for i in range(self.M):if self.y[i]==-1:plt.plot(self.X[0,i],self.X[1,i],'or')elif self.y[i]==1:plt.plot(self.X[0,i],self.X[1,i],'ob')for i in self.supportVec:plt.plot(self.X[0,i],self.X[1,i],'oy')plt.show()试验一下结果:
使用类似如下的代码:
svms=SVMC(X,y,kernel=Gauss_kernel)
svms.train()
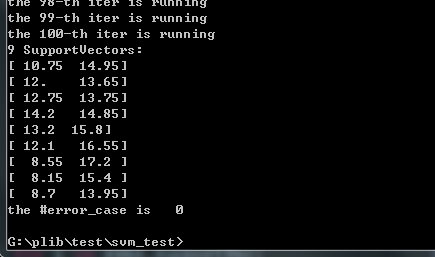
print len(svms.supportVec),"SupportVectors:"for i in range(len(svms.supportVec)):t=svms.supportVec[i]print svms.X[:,t]
svms.error(X,y)线性的:
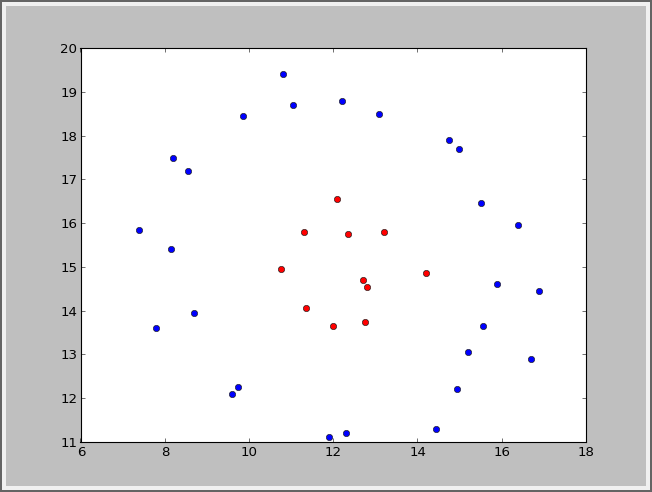
高斯的:你要自己写个高斯核
def Gauss_kernel(x,z,sigma=1):return np.exp(-np.sum((x-z)**2)/(2*sigma**2))
svms=SVMC(X,y,kernel=Gauss_kernel)结果:
五.参考
【1】《统计学习方法》
【2】 JerryLead 的五篇
【3】一个Java的实现 :点击打开链接