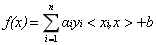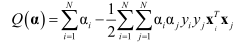基于最大间隔分隔数据
1.1支持向量与超平面
SVM(Support Vector Mac)又称为支持向量机,是一种二分类的模型。当然如果进行修改之后也是可以用于多类别问题的分类。支持向量机可以分为线性核和非线性两大类。其主要思想为找到空间中的一个更够将所有数据样本划开的超平面,并且使得本集中所有数据到这个超平面的距离最短。
在了解SVM算法之前,我们首先需要了解一下线性分类器这个概念。比如给定一系列的数据样本,每个样本都有对应的一个标签。为了使得描述更加直观,我们采用二维平面进行解释,高维空间原理也是一样。举个简单子:如下图所示是一个二维平面,平面上有两类不同的数据,分别用圆圈和方块表示。我们可以很简单地找到一条直线使得两类数据正好能够完全分开。但是能将据点完全分割开的直线不止一条,那么在如此众多的直线中我们应该选择哪一条呢?我们希望寻找到这样的一条分割线,使得距离这条直线的点到这条直线的距离最短。从下图直观来解释就是要求两条外面的线之间的间隔最大。这是可以理解的,因为假如数据样本是随机出现的,那么这样分割之后数据点落入到其类别一侧的概率越高那么最终预测的准确率也会越高。在高维空间中这样的直线称之为超平面,因为当维数大于三的时候我们已经无法想象出这个平面的具体样子。那些距离这个超平面最近的点就是所谓支持向量,实际上如果确定了支持向量也就确定了这个超平面,找到这些支持向量之后其他样本就不会起作用了。

1.2寻找最大间隔
1.2.1点到超平面的距离公式
既然这样的直线是存在的,那么我们怎样寻找出这样的直线呢?与二维空间类似,超平面的方程也可以写成一下形式:
w T x + b = 0 (1) w^Tx+b=0\tag{1} wTx+b=0(1)
有了超平面的表达式之后之后,我们就可以计算样本点到平面的距离了。假设 P ( x 1 , x 2 . . . x n ) P(x_1,x_2...x_n) P(x1,x2...xn)为样本的中的一个点,其中 x i x_i xi表示为第个特征变量。那么该点到超平面的距离 d d d就可以用如下公式进行计算:
d = ∣ ∑ i = 1 n w i x i + b ∣ ∣ ∣ w ∣ ∣ (2) d=\frac{|\sum_{i=1}^nw_ix_i+b|}{||w||}\tag{2} d=∣∣w∣∣∣∑i=1nwixi+b∣(2)
其中 ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣为超平面的2范数,即 w w w向量的模长。
上面的公式可以利用解析几何或高中平面几何知识进行推导,这里不做进一步解释。
1.2.2最大间隔的优化模型
现在我们已经知道了如何去求数据点到超平面的距离,在超平面确定的情况下,我们就能够找出所有支持向量,然后计算出间隔margin。每一个超平面都对应着一个margin,我们的目标就是找出所有margin中最大的那个值对应的超平面。因此用数学语言描述就是确定w、b使得margin最大。这是一个优化问题其目标函数可以写成:
a r g m a x w , b ( m i n ( y ( w T x + b ) ) ∗ 1 ∣ ∣ w ∣ ∣ ) (3) arg\quad max_{w,b}(min(y(w^Tx+b))*\frac{1}{||w||})\tag{3} argmaxw,b(min(y(wTx+b))∗∣∣w∣∣1)(3)
其中 y y y表示数据点的标签,当它为+1时为正例,为-1时为负例。在进行距离计算时乘以 y y y,可以使数据点在平面的正方向(即+1类)是一个正数,而当数据点在平面的负方向时(即-1类),依然是一个正数,这样就能够保证始终大于零了。注意到当 w w w和 b b b等比例放大时, d d d的结果是不会改变的。令 u = y ( w T x + b ) u=y(w^Tx+b) u=y(wTx+b),因此我们可以令所有支持向量的 u u u为1,而其他点的 u u u大于1这是可以办通过调节 w w w和 b b b求到的。因此上面的问题可以简化为:
a r g m a x 1 ∣ ∣ w ∣ ∣ s . t . y ( w T x + b ) − 1 ≥ 0 (4) arg\quad max\frac{1}{||w||}\tag{4}\\ s.t. \quad y(w^Tx+b)-1\geq 0 argmax∣∣w∣∣1s.t.y(wTx+b)−1≥0(4)
为了后面计算的方便,我们将目标函数等价替换为:
m i n 1 2 ∣ ∣ w ∣ ∣ 2 (5) min\frac{1}{2}||w||^2\tag{5} min21∣∣w∣∣2(5)
这是一个有约束条件的优化问题,通常我们可以用拉格朗日乘子法来求解。拉格朗日乘子法即高数里面的求条件极值,此处的 α i α_i αi即为条件极值里面的 λ i λ_i λi。SVM的主要工作就是求解这些 α i α_i αi,一旦求出所有α,那么分割超平面就可以用这些α来表示。应用拉格朗日乘子法如下,令:
L ( w , b , α ) = 1 2 ∣ ∣ w ∣ ∣ 2 − ∑ i = 1 n α i ( y i ( w x i + b ) − 1 ) (6) L(w,b,\alpha)=\frac{1}{2}||w||^2-\sum_{i=1}^n\alpha_i(y_i(wx_i+b)-1)\tag{6} L(w,b,α)=21∣∣w∣∣2−i=1∑nαi(yi(wxi+b)−1)(6)
求 L L L关于 w w w和 b b b的偏导:
{ ∂ L ∂ w = 0 ⇒ w = ∑ i = 1 n α i y i x i ∂ L ∂ b = 0 ⇒ ∑ i = 1 n α i y i = 0 (7) \begin{cases}\frac{\partial L}{\partial w}=0\Rightarrow w= \sum_{i=1}^{n}\alpha_iy_ix_i \\\frac{\partial L}{\partial b}=0\Rightarrow \sum_{i=1}^{n}\alpha _iy_i=0\end{cases}\tag{7} {∂w∂L=0⇒w=∑i=1nαiyixi∂b∂L=0⇒∑i=1nαiyi=0(7)
将(7)代入到(6)中消去 w w w, b b b化简得:
L ( α ) = ∑ i = 1 n α i − 1 2 ∑ i , j = 1 n α i α j y i y j x i T x j (8) L(\alpha)=\sum_{i=1}^n\alpha_i-\frac{1}{2}\sum_{i,j=1}^n\alpha_i\alpha_jy_iy_jx_i^Tx_j\tag{8} L(α)=i=1∑nαi−21i,j=1∑nαiαjyiyjxiTxj(8)
则化为求原问题的对偶问题:
m a x L ( α ) = ∑ i = 1 n α i − 1 2 ∑ i , j = 1 n α i α j y i y j x i T x j s . t . { ∑ i = 1 n α i y i = 0 α i ≥ 0 (9) max\quad L(\alpha)=\sum_{i=1}^n\alpha_i-\frac{1}{2}\sum_{i,j=1}^n\alpha_i\alpha_jy_iy_jx_i^Tx_j\\ s.t.\quad \begin{cases}\sum_{i=1}^n\alpha_iy_i=0\\ \alpha_i\geq0 \end{cases}\tag{9} maxL(α)=i=1∑nαi−21i,j=1∑nαiαjyiyjxiTxjs.t.{∑i=1nαiyi=0αi≥0(9)
该对偶问题的KKT条件为:
{ α i ≥ 0 y i ( w i x i + b ) − 1 ≥ 0 α i ( y i ( w i x i + b ) − 1 ) = 0 (10) \begin{cases}\alpha_i\geq0\\y_i(w_ix_i+b)-1\geq0\\\alpha_i(y_i(w_ix_i+b)-1)=0 \end{cases}\tag{10} ⎩ ⎨ ⎧αi≥0yi(wixi+b)−1≥0αi(yi(wixi+b)−1)=0(10)
到此,似乎问题就能够完美地解决了。但是这里有个假设:数据必须是百分之百可分的。但是实际中的数据几乎都不那么“干净”,或多或少都会存在一些噪点。为此下面我们将引入了松弛变量来解决这种问题。
1.2.3松弛变量
由上一节的分析我们知道实际中很多样本数据都不能够用一个超平面把数据完全分开。如果数据集中存在噪点的话,那么在求超平的时候就会出现很大问题。从图2中可看出其中一个蓝点偏差太大,如果把它作为支持向量的话所求出来的margin就会比不算入它时要小得多。更糟糕的情况是如果这个蓝点落在了红点之间那么就找不出超平面了。

因此引入一个松弛变量ξ来允许一些数据可以处于分隔面错误的一侧。这时新的约束条件变为:
y i ( w T x i + b ) ≥ 1 − ξ i (11) y_i(w^Tx_i+b)\geq1-\xi_i\tag{11} yi(wTxi+b)≥1−ξi(11)
式中 ξ i \xi_i ξi的含义为允许第i个数据点允许偏离的间隔。如果让 ξ ξ ξ任意大的话,那么任意的超平面都是符合条件的了。所以在原有目标的基础之上,我们也尽可能的让 ξ ξ ξ的总量也尽可能地小。所以新的目标函数变为:
m i n 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 n ξ i s . t . y i ( w T x i + b ) ≥ 1 − ξ i a n d ξ i ≥ 0 (12) min\quad \frac{1}{2}||w||^2+C\sum_{i=1}^n\xi_i\tag{12} \\s.t.\quad y_i(w^Tx_i+b)\geq1-\xi_i\quad and\quad \xi_i\geq0 min21∣∣w∣∣2+Ci=1∑nξis.t.yi(wTxi+b)≥1−ξiandξi≥0(12)
其中的C是用于控制“最大化间隔”和“保证大部分的点的函数间隔都小于1”这两个目标的权重。
则新的拉格朗日函数变为:
L ( w , b , ξ i , α , τ ) = 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 n ξ i − ∑ i = 1 n α i ( y i ( w T x i + b ) ≥ 1 − ξ i ) − ∑ i = 1 n τ i ξ i (13) L(w,b,\xi_i,\alpha,\tau)=\frac{1}{2}||w||^2+C\sum_{i=1}^n\xi_i-\sum_{i=1}^n\alpha_i(y_i(w^Tx_i+b)\geq1-\xi_i)-\sum_{i=1}^n\tau_i\xi_i\tag{13} L(w,b,ξi,α,τ)=21∣∣w∣∣2+Ci=1∑nξi−i=1∑nαi(yi(wTxi+b)≥1−ξi)−i=1∑nτiξi(13)
接下来将拉格朗日函数转化为其对偶函数,首先对分别求ξ的偏导,并令其为0,结果如下:
{ ∂ L ∂ w = 0 ⇒ w = ∑ i = 1 n α i y i x i ∂ L ∂ b = 0 ⇒ ∑ i = 1 n α i y i = 0 ∂ L ∂ ξ i = 0 ⇒ C − α i − τ i = 0 (14) \begin{cases}\frac{\partial L}{\partial w}=0\Rightarrow w= \sum_{i=1}^{n}\alpha_iy_ix_i \\\frac{\partial L}{\partial b}=0\Rightarrow \sum_{i=1}^{n}\alpha _iy_i=0\\\frac{\partial L}{\partial \xi_i}=0\Rightarrow C-\alpha_i-\tau_i=0 \end{cases}\tag{14} ⎩ ⎨ ⎧∂w∂L=0⇒w=∑i=1nαiyixi∂b∂L=0⇒∑i=1nαiyi=0∂ξi∂L=0⇒C−αi−τi=0(14)
代入原式化简之后得到和原来一样的目标函数:
m a x L ( α ) = ∑ i = 1 n α i − 1 2 ∑ i , j = 1 n α i α j y i y j x i T x j (15) max\quad L(\alpha)=\sum_{i=1}^n\alpha_i-\frac{1}{2}\sum_{i,j=1}^n\alpha_i\alpha_jy_iy_jx_i^Tx_j\tag{15} maxL(α)=i=1∑nαi−21i,j=1∑nαiαjyiyjxiTxj(15)
但是由于我们得到 C − α i − τ i = 0 C-\alpha_i-\tau_i=0 C−αi−τi=0而 τ i ≥ 0 \tau_i\geq0 τi≥0,因此有 α i ≤ C \alpha_i\leq C αi≤C,所以对偶问题写成:
L ( α ) = ∑ i = 1 n α i − 1 2 ∑ i , j = 1 n α i α j y i y j x i T x j s . t . C ≥ α i ≥ 0 a n d ∑ i = 1 n α i y i = 0 (16) L(\alpha)=\sum_{i=1}^n\alpha_i-\frac{1}{2}\sum_{i,j=1}^n\alpha_i\alpha_jy_iy_jx_i^Tx_j\tag{16} \\s.t.\quad C\geq \alpha_i\geq0\quad and \quad \sum_{i=1}^{n}\alpha_iy_i=0 L(α)=i=1∑nαi−21i,j=1∑nαiαjyiyjxiTxjs.t.C≥αi≥0andi=1∑nαiyi=0(16)
经过添加松弛变量的方法,我们现在能够解决数据更加混乱的问题。通过修改参数C,我们可以得到不同的结果而C的大小到底取多少比较合适,需要根据实际问题进行调节。
1.2.4核函数
以上讨论的都是在线性可分情况进行讨论的,但是实际问题中给出的数据并不是都是线性可分的,比如有些数据可能是如图3样子。

那么这种非线性可分的数据是否就不能用SVM算法来求解呢?答案是否定的。事实上对于低维平面内不可分的数据,放在一个高维空间中去就有可能变得可分。以二维平面的数据为例,我们可以通过找到一个映射将二维平面的点放到三维平面之中。理论上任意的数据样本都能够找到一个合适的映射使得这些在低维空间不能划分的样本到高维空间中之后能够线性可分。
定义一个映射使得将所有映射到更高维空间之后等价于求解问题(9)的对偶问题:
m a x L ( α ) = ∑ i = 1 n α i − 1 2 ∑ i , j = 1 n α i α j y i y j < ϕ ( x i ) , ϕ ( x j ) > s . t . { ∑ i = 1 n α i y i = 0 C ≥ α i ≥ 0 (17) max\quad L(\alpha)=\sum_{i=1}^n\alpha_i-\frac{1}{2}\sum_{i,j=1}^n\alpha_i\alpha_jy_iy_j<\phi(x_i),\phi(x_j)>\\ s.t.\quad \begin{cases}\sum_{i=1}^n\alpha_iy_i=0\\ C\geq\alpha_i\geq0 \end{cases}\tag{17} maxL(α)=i=1∑nαi−21i,j=1∑nαiαjyiyj<ϕ(xi),ϕ(xj)>s.t.{∑i=1nαiyi=0C≥αi≥0(17)
这样对于线性不可分的问题就解决了,现在只需要找出一个合适的映射即可。当特征变量非常多的时候在,高维空间中计算内积的运算量是非常庞大的。考虑到我们的目的并不是为找到这样一个映射而是为了计算其在高维空间的内积,因此如果我们能够找到计算高维空间下内积的公式,那么就能够避免这样庞大的计算量,我们的问题也就解决了。实际上这就是我们要找的核函数 κ ( x i , x j ) \kappa(x_i,x_j) κ(xi,xj),即两个向量在隐式映射后的空间中的内积。
那么怎样的函数才可以作为核函数呢?下面的一个定理可以帮助我们判断。
Mercer定理:任何半正定的函数都可以作为核函数。其中所谓半正定函数 f ( x i , x j ) f(x_i,x_j) f(xi,xj)是指拥有训练集数据集合,我们定义一个矩阵的元素 a i j = f ( x i , x j ) a_{ij}=f(x_i,x_j) aij=f(xi,xj),这个矩阵是 C n × n C^{n\times n} Cn×n的矩阵,如果这个矩阵是半正定的,那么称该矩阵为半正定函数。
值得注意的是,上述定理中所给出的条件是充分条件而非充要条件。因为有些非正定函数也可以作为核函数。
下面是一些常用的核函数:
| 函数名 | 核函数表达式 | 函数名 | 核函数表达式 |
|---|---|---|---|
| 线性核 | κ ( x , y ) = x T y \kappa(x,y)=x^Ty κ(x,y)=xTy | 指数核 | κ ( x , y ) = e x p ( − ∣ x − y ∣ 2 σ 2 ) \kappa(x,y)=exp(-\frac{\mid x-y\mid}{2\sigma^2}) κ(x,y)=exp(−2σ2∣x−y∣) |
| 多项式核 | κ ( x , y ) = ( a x T y + c ) d \kappa(x,y)=(ax^Ty+c)^d κ(x,y)=(axTy+c)d | 拉普拉斯核 | κ ( x , y ) = e x p ( − ∣ x − y ∣ σ ) \kappa(x,y)=exp(-\frac{\mid x-y\mid}{\sigma}) κ(x,y)=exp(−σ∣x−y∣) |
| 高斯核 | κ ( x , y ) = e x p ( − ( x − y ) 2 2 σ 2 ) \kappa(x,y)=exp(-\frac{(x-y)^2}{2\sigma^2}) κ(x,y)=exp(−2σ2(x−y)2) | Sigmoid核 | κ ( x , y ) = t a n h ( a x T y + c ) \kappa(x,y)=tanh(ax^Ty+c) κ(x,y)=tanh(axTy+c) |
现在我们已经了解了一些支持向量机的理论基础,我们通过对偶问题的的转化将最开始求 w , b w,b w,b的问题转化为求 α \alpha α的对偶问题。只要找到所有的 α \alpha α(即找出所有支持向量),我们就能够确定 w , b w,b w,b。然后就可以通过计算数据点到这个超平面的距离从而判断出该数据点的类别。
1.3 SVM的Python实现
#svm算法的实现
from numpy import*
import random
from time import*
def loadDataSet(fileName):#输出dataArr(m*n),labelArr(1*m)其中m为数据集的个数dataMat=[];labelMat=[]fr=open(fileName)for line in fr.readlines():lineArr=line.strip().split('\t')#去除制表符,将数据分开dataMat.append([float(lineArr[0]),float(lineArr[1])])#数组矩阵labelMat.append(float(lineArr[2]))#标签return dataMat,labelMatdef selectJrand(i,m):#随机找一个和i不同的jj=iwhile(j==i):j=int(random.uniform(0,m))return jdef clipAlpha(aj,H,L):#调整大于H或小于L的alpha的值if aj>H:aj=Hif aj<L:aj=Lreturn ajdef smoSimple(dataMatIn,classLabels,C,toler,maxIter):dataMatrix=mat(dataMatIn);labelMat=mat(classLabels).transpose()#转置b=0;m,n=shape(dataMatrix)#m为输入数据的个数,n为输入向量的维数alpha=mat(zeros((m,1)))#初始化参数,确定m个alphaiter=0#用于计算迭代次数while (iter<maxIter):#当迭代次数小于最大迭代次数时(外循环)alphaPairsChanged=0#初始化alpha的改变量为0for i in range(m):#内循环fXi=float(multiply(alpha,labelMat).T*\(dataMatrix*dataMatrix[i,:].T))+b#计算f(xi)Ei=fXi-float(labelMat[i])#计算f(xi)与标签之间的误差if ((labelMat[i]*Ei<-toler)and(alpha[i]<C))or\((labelMat[i]*Ei>toler)and(alpha[i]>0)):#如果可以进行优化j=selectJrand(i,m)#随机选择一个j与i配对fXj=float(multiply(alpha,labelMat).T*\(dataMatrix*dataMatrix[j,:].T))+b#计算f(xj)Ej=fXj-float(labelMat[j])#计算j的误差alphaIold=alpha[i].copy()#保存原来的alpha(i)alphaJold=alpha[j].copy()if(labelMat[i]!=labelMat[j]):#保证alpha在0到c之间L=max(0,alpha[j]-alpha[i])H=min(C,C+alpha[j]-alpha[i])else:L=max(0,alpha[j]+alpha[i]-C)H=min(C,alpha[j]+alpha[i])if L==H:print('L=H');continueeta=2*dataMatrix[i,:]*dataMatrix[j,:].T-\dataMatrix[i,:]*dataMatrix[i,:].T-\dataMatrix[j,:]*dataMatrix[j,:].Tif eta>=0:print('eta=0');continuealpha[j]-=labelMat[j]*(Ei-Ej)/etaalpha[j]=clipAlpha(alpha[j],H,L)#调整大于H或小于L的alphaif (abs(alpha[j]-alphaJold)<0.0001):print('j not move enough');continuealpha[i]+=labelMat[j]*labelMat[i]*(alphaJold-alpha[j])b1=b-Ei-labelMat[i]*(alpha[i]-alphaIold)*\dataMatrix[i,:]*dataMatrix[i,:].T-\labelMat[j]*(alpha[j]-alphaJold)*\dataMatrix[i,:]*dataMatrix[j,:].T#设置bb2=b-Ej-labelMat[i]*(alpha[i]-alphaIold)*\dataMatrix[i,:]*dataMatrix[i,:].T-\labelMat[j]*(alpha[j]-alphaJold)*\dataMatrix[j,:]*dataMatrix[j,:].Tif (0<alpha[i])and(C>alpha[j]):b=b1elif(0<alpha[j])and(C>alpha[j]):b=b2else:b=(b1+b2)/2alphaPairsChanged+=1print('iter:%d i:%d,pairs changed%d'%(iter,i,alphaPairsChanged))if (alphaPairsChanged==0):iter+=1else:iter=0print('iteraction number:%d'%iter)return b,alpha
#定义径向基函数
def kernelTrans(X, A, kTup):#定义核转换函数(径向基函数)m,n = shape(X)K = mat(zeros((m,1)))if kTup[0]=='lin': K = X * A.T #线性核K为m*1的矩阵elif kTup[0]=='rbf':for j in range(m):deltaRow = X[j,:] - AK[j] = deltaRow*deltaRow.TK = exp(K/(-1*kTup[1]**2)) #divide in NumPy is element-wise not matrix like Matlabelse: raise NameError('Houston We Have a Problem -- \That Kernel is not recognized')return Kclass optStruct:def __init__(self,dataMatIn, classLabels, C, toler, kTup): # Initialize the structure with the parametersself.X = dataMatInself.labelMat = classLabelsself.C = Cself.tol = tolerself.m = shape(dataMatIn)[0]self.alphas = mat(zeros((self.m,1)))self.b = 0self.eCache = mat(zeros((self.m,2))) #first column is valid flagself.K = mat(zeros((self.m,self.m)))for i in range(self.m):self.K[:,i] = kernelTrans(self.X, self.X[i,:], kTup)def calcEk(oS, k):fXk = float(multiply(oS.alphas,oS.labelMat).T*oS.K[:,k] + oS.b)Ek = fXk - float(oS.labelMat[k])return Ekdef selectJ(i, oS, Ei):maxK = -1; maxDeltaE = 0; Ej = 0oS.eCache[i] = [1,Ei]validEcacheList = nonzero(oS.eCache[:,0].A)[0]if (len(validEcacheList)) > 1:for k in validEcacheList: #loop through valid Ecache values and find the one that maximizes delta Eif k == i: continue #don't calc for i, waste of timeEk = calcEk(oS, k)deltaE = abs(Ei - Ek)if (deltaE > maxDeltaE):maxK = k; maxDeltaE = deltaE; Ej = Ekreturn maxK, Ejelse: #in this case (first time around) we don't have any valid eCache valuesj = selectJrand(i, oS.m)Ej = calcEk(oS, j)return j, Ejdef updateEk(oS, k):#after any alpha has changed update the new value in the cacheEk = calcEk(oS, k)oS.eCache[k] = [1,Ek]def innerL(i, oS):Ei = calcEk(oS, i)if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):j,Ej = selectJ(i, oS, Ei) #this has been changed from selectJrandalphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy()if (oS.labelMat[i] != oS.labelMat[j]):L = max(0, oS.alphas[j] - oS.alphas[i])H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])else:L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)H = min(oS.C, oS.alphas[j] + oS.alphas[i])if L==H: print("L==H"); return 0eta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j] #changed for kernelif eta >= 0: print("eta>=0"); return 0oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/etaoS.alphas[j] = clipAlpha(oS.alphas[j],H,L)updateEk(oS, j) #added this for the Ecacheif (abs(oS.alphas[j] - alphaJold) < 0.00001): print("j not moving enough"); return 0oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])#update i by the same amount as jupdateEk(oS, i) #added this for the Ecache #the update is in the oppostie directionb1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i] - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j]- oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2else: oS.b = (b1 + b2)/2.0return 1else: return 0
#smoP函数用于计算超平的alpha,b
def smoP(dataMatIn, classLabels, C, toler, maxIter,kTup=('lin', 0)): #完整的Platter SMOoS = optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler, kTup)iter = 0#计算循环的次数entireSet = True; alphaPairsChanged = 0while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):alphaPairsChanged = 0if entireSet: #go over allfor i in range(oS.m):alphaPairsChanged += innerL(i,oS)print("fullSet, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))iter += 1else:#go over non-bound (railed) alphasnonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]for i in nonBoundIs:alphaPairsChanged += innerL(i,oS)print("non-bound, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))iter += 1if entireSet: entireSet = False #toggle entire set loopelif (alphaPairsChanged == 0): entireSet = Trueprint("iteration number: %d" % iter)return oS.b,oS.alphas
#calcWs用于计算权重值w
def calcWs(alphas,dataArr,classLabels):#计算权重WX = mat(dataArr); labelMat = mat(classLabels).transpose()m,n = shape(X)w = zeros((n,1))for i in range(m):w += multiply(alphas[i]*labelMat[i],X[i,:].T)return w#值得注意的是测试准确与k1和C的取值有关。
def testRbf(k1=1.3):#给定输入参数K1#测试训练集上的准确率dataArr,labelArr = loadDataSet('testSetRBF.txt')#导入数据作为训练集b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, ('rbf', k1)) #C=200 importantdatMat=mat(dataArr); labelMat = mat(labelArr).transpose()svInd=nonzero(alphas.A>0)[0]#找出alphas中大于0的元素的位置#此处需要说明一下alphas.A的含义sVs=datMat[svInd] #获取支持向量的矩阵,因为只要alpha中不等于0的元素都是支持向量labelSV = labelMat[svInd]#支持向量的标签print("there are %d Support Vectors" % shape(sVs)[0])#输出有多少个支持向量m,n = shape(datMat)#数据组的矩阵形状表示为有m个数据,数据维数为nerrorCount = 0#计算错误的个数for i in range(m):#开始分类,是函数的核心kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))#计算原数据集中各元素的核值predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b#计算预测结果y的值if sign(predict)!=sign(labelArr[i]): errorCount += 1#利用符号判断类别### sign(a)为符号函数:若a>0则输出1,若a<0则输出-1.###print("the training error rate is: %f" % (float(errorCount)/m))#2、测试测试集上的准确率dataArr,labelArr = loadDataSet('testSetRBF2.txt')errorCount = 0datMat=mat(dataArr)#labelMat = mat(labelArr).transpose()此处可以不用m,n = shape(datMat)for i in range(m):kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + bif sign(predict)!=sign(labelArr[i]): errorCount += 1print("the test error rate is: %f" % (float(errorCount)/m))
def main():t1=time()dataArr,labelArr=loadDataSet('testSet.txt')b,alphas=smoP(dataArr,labelArr,0.6,0.01,40)ws=calcWs(alphas,dataArr,labelArr)testRbf()t2=time()print("程序所用时间为%ss"%(t2-t1))if __name__=='__main__':main()