1.签名的意义
　　为了保证每个应用程序开发商合法ID，防止部分开放商可能通过使用相同的Package Name来混淆替换已经安装的程序，我们需要对我们发布的APK文件进行唯一签名，保证我们每次发布的版本的一致性(如自动更新不会因为版本不一致而无法安装)。

2.签名的步骤
　　a.创建key
　　b.使用步骤a中产生的key对apk签名

3.具体操作

　　方法一： 命令行下对apk签名（原理）
　　创建key，需要用到keytool.exe (位于jdk1.6.0_24jre\bin目录下)，使用产生的key对apk签名用到的是jarsigner.exe (位于jdk1.6.0_24\bin目录下)，把上两个软件所在的目录添加到环境变量path后，打开cmd输入

         D:>keytool -genkey -alias demo.keystore -keyalg RSA -validity 40000

        -keystore demo.keystore
/*说明：-genkey 产生密钥
-alias demo.keystore 别名 demo.keystore
-keyalg RSA 使用RSA算法对签名加密
-validity 40000 有效期限4000天
-keystore demo.keystore */
D:>jarsigner -verbose -keystore demo.keystore -signedjar demo_signed.apk 

         demo.apk demo.keystore
/*说明：-verbose 输出签名的详细信息
-keystore  demo.keystore 密钥库位置
-signedjar demor_signed.apk demo.apk demo.keystore 正式签名，三个参数中

依次为签名后产生的文件demo_signed，要签名的文件demo.apk和密钥库demo.keystore.*/

　　注意事项：android工程的bin目录下的demo.apk默认是已经使用debug用户签名的，所以不能使用上述步骤对此文件再次签名。正确步骤应该是:在工程点击右键->Anroid Tools-Export Unsigned Application Package导出的apk采用上述步骤签名。

　　方法二：使用Eclipse导出带签名的apk
　　Eclipse直接能导出带签名的最终apk，非常方便，推荐使用，步骤如下：
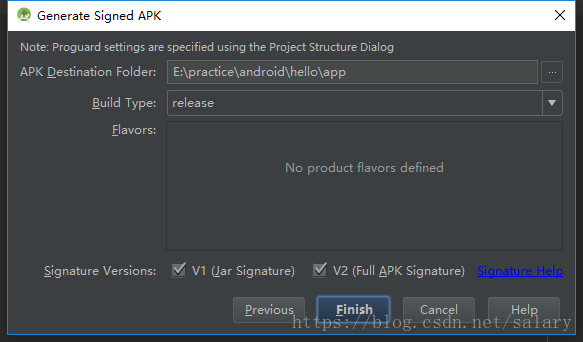
　　第一步：导出。
 
　　第二步：创建密钥库keystore,输入密钥库导出位置和密码，记住密码，下次Use existing keystore会用到。
 
　　第三步：填写密钥库信息，填写一些apk文件的密码，使用期限和组织单位的信息。

　　第四步：生成带签名的apk文件，到此就结束了。

　　第五步：如果下次发布版本的时候，使用前面生成的keystore再签名。

　　第六步：下一步，下一步，然后就OK了！

　　方法三：使用IntelliJ IDEA导出带签名的apk 
　　方法步骤基本和Eclipse相同，大概操作路径是：菜单Tools->Andrdoid->Export signed apk。

4.签名之后，用zipalign(压缩对齐)优化你的APK文件。
　　未签名的apk不能使用，也不能优化。签名之后的apk谷歌推荐使用zipalign.exe(位于android-sdk-windows ools目录下)工具对其优化：

       D:>zipalign -v 4 demo_signed.apk final.apk

　　如上，zipalign能够使apk文件中未压缩的数据在4个字节边界上对齐（4个字节是一个性能很好的值），这样android系统就可以使用mmap()(请自行查阅这个函数的用途)函数读取文件，可以在读取资源上获得较高的性能，
　　PS:1.在4个字节边界上对齐的意思就是，一般来说，是指编译器吧4个字节作为一个单位来进行读取的结果，这样的话，CPU能够对变量进行高效、快速的访问（较之前不对齐）。
          2.对齐的根源：android系统中的Davlik虚拟机使用自己专有的格式DEX，DEX的结构是紧凑的，为了让运行时的性能更好，可以进一步用"对齐"进一步优化，但是大小一般会有所增加。

5.签名对你的App的影响。
　　 你不可能只做一个APP，你可能有一个宏伟的战略工程，想要在生活，服务，游戏，系统各个领域都想插足的话，你不可能只做一个APP，谷歌建议你把你所有的APP都使用同一个签名证书。
　　 使用你自己的同一个签名证书，就没有人能够覆盖你的应用程序，即使包名相同，所以影响有：
　　1) App升级。 使用相同签名的升级软件可以正常覆盖老版本的软件，否则系统比较发现新版本的签名证书和老版本的签名证书不一致，不会允许新版本安装成功的。
　　2) App模块化。android系统允许具有相同的App运行在同一个进程中，如果运行在同一个进程中，则他们相当于同一个App，但是你可以单独对他们升级更新，这是一种App级别的模块化思路。
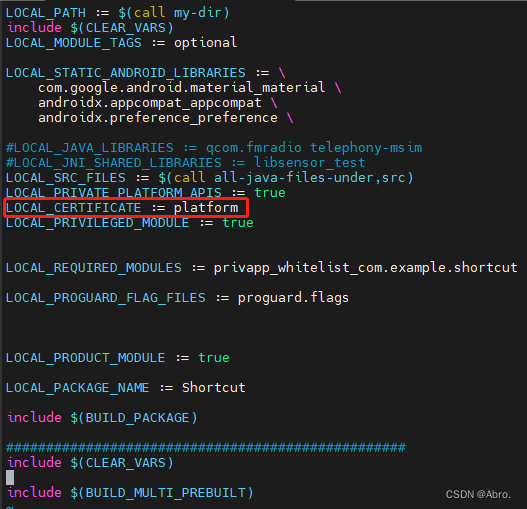
　　3) 允许代码和数据共享。android中提供了一个基于签名的Permission标签。通过允许的设置，我们可以实现对不同App之间的访问和共享，如下：

        AndroidManifest.xml：<permission android:protectionLevel="normal" />