Android APP的签名
Android项目以它的包名作为唯一的标识,如果在同一部手机上安装两个包名相同的APP,后者就会覆盖前面安装的应用。为了避免Android APP被随意覆盖,Android要求对APP进行签名。下面介绍对APP进行签名的步骤
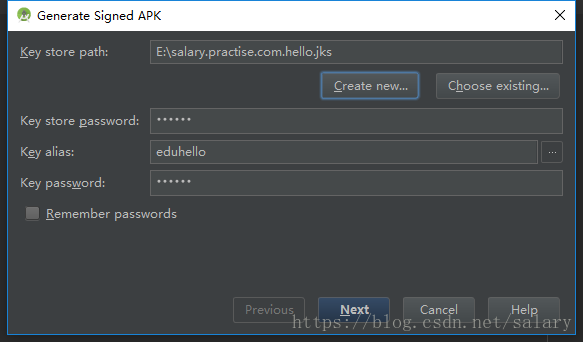
1、选择builder菜单下的Generate Signed APK
2、弹出签名向导对话框
3、在该对话框中选择数字证书,如果没有数字证书,可以点击Create new按钮,创建数字证书如下图所示:
4、输入证书的存储路径及文件名称,密码,有效年份,发布人员的姓名,单位,所在城市,省份,国家等信息,后点击OK按钮,如下图所示,系统会自动带入密码
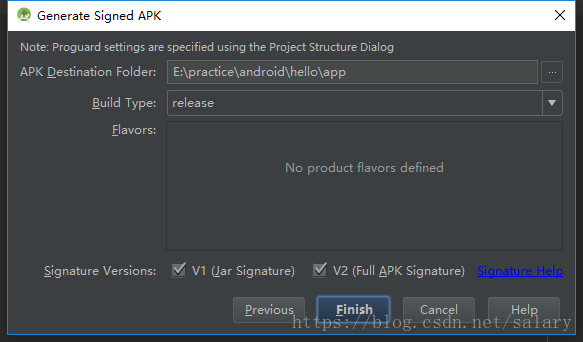
5、点击Next选择签名后的安装包存放路径,构建类型,点击finish完成安装包的构建
注意:
- v2是Android 7.0中引入了签名版本,v1是jar Signature来自JDK,只勾选v1签名并不会影响什么,但是在7.0上不会使用更安全的验证方式,只勾选V2签名7.0以下会直接安装完显示未安装,7.0以上则使用了V2的方式验证,为了保证兼容性,可以同时勾选V1和V2。
- 在Debug调试版本中,默认会调用调试用的签名证书debug.keystore,该证书默认存放在C:\Users\<你的用户名>\.android下。
- 包名和签名都相同的APP才可以覆盖安装
(张伟:2018年9月1日)
(转载时请注明来源)