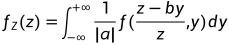卷积公式的推导过程书上有，不难理解。但是在解题时，确定积分区间很是头疼，本文讲解如何确定积分区间。

首先弄清f是什么，从定义入手，对于二维连续型随机变量（X,Y），Z=X+Y有 

F(z)是一个二重积分，高数下册中求解二重积分用的是“平行截面法”，所以f(z)就相当于是第一次积分的平行截面的面积A(z)。相当于“先积x”

接下来确定此二重积分的积分区域，方法是把题设取值范围中的y换成z-x。

和求二重积分相比较，我们是求第一次积分后的结果，而不是求最终结果，所以f要分段。

结论：f(z)分段的原则就是使积分上下限不同。即以x为横轴，z为纵轴，画一条横线，穿过不同的积分边界。 

解释下原因：

F(z)={z<=z}要考虑到所有可能的取值，F(z)分段，所以f(z)也分段，又F(z)是f(z)的原函数，所以f(z)分段时z的区间和F(z)分段时z的区间保持一致。

f(z)在本身的积分区域上有定义，所以f(z)最后的积分区域还要求一次交集。

所以，相当于是从积分的角度理解为什么要分段。而分段的本质是分布函数分段，即分布函数覆盖了取常数的概率值。

最终得到用卷积公式求f的解题步骤为：

1.画出新的积分区域。根据y的取值及x，z与y的关系，把x，y的积分区域转变为x，z的积分区域

2.计算积分