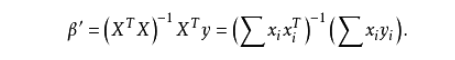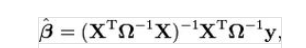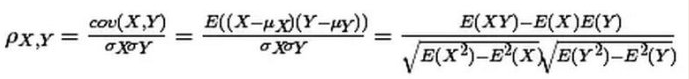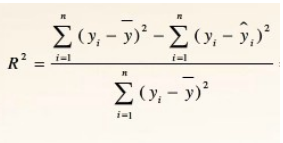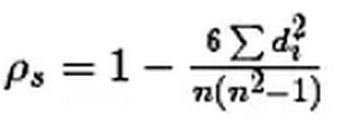文章目录
- 1、术语
- 2、UnivariateStatistic: 单变量统计分析
- 3、Frequency distributions:频率分布
- 4、Simple regression : 简单回归
- 5、Multiple linear regression:多元线性回归
- 6、Rank transformations :
- 7、Covariance and correlation: 协方差和相关性
- PearsonsCorrelation : 皮尔逊相关
- SpearmanCorrelation : 斯皮尔曼相关性
- 8、Statistical tests : 统计检验
1、术语
| 英文 | 中文 |
|---|---|
| arithmetic and geometric means | 算术和几何平均值 |
| variance and standard deviation | 方差与标准差 |
| sum, product, log sum, sum of squared values | 和、积、对数、平方值和 |
| minimum, maximum, median, and percentiles | 最小值、最大值、中位数、百分比 |
| skewness and kurtosis | 偏态和峰度 |
| first, second, third and fourth moments | 第一、第二、第三和第四时刻 |
| UnivariateStatistic | 单变量统计分析 |
| covariance matrix | 协方差矩阵 |
| rolling mean | 滚动平均值 |
| Frequency distributions | 频率分布 |
| cumulative percentage | 累计百分比 |
| least squares regression | 最小二乘回归 |
| independent variable | 自变量、独立变量 |
| dependent variable | 因变量 |
| Standard errors | 标准误 |
| intercept, slope | 截距, 斜度 |
| inference statistics | 统计推断 |
| Multiple linear regression | 多元线性回归 |
| regressor | 回归因子 |
| non-bias-corrected | 非偏差校正 |
2、UnivariateStatistic: 单变量统计分析
UnivariateStatistic 是顶级接口,包含 evalute() 接口方法,接收 double[] 输入参数,返回统计结果;
public interface UnivariateStatistic extends MathArrays.Function {double evaluate(double[] values) throws MathIllegalArgumentException;double evaluate(double[] values, int begin, int length) throws MathIllegalArgumentException;
}
每一类统计方式有独立的实现类,放在 rank,summary,moment 三个包中。可以通过直接实例化相应的统计类,来使用它们,也可以通过 DescriptiveStatistics 和 SummaryStatistics 这样的工厂类来使用。
| Aggregate | Statistics included | Values stored? | “Rolling” capability |
|---|---|---|---|
| DescriptiveStatistics | min, max, mean, geometric mean, n, sum, sum of squares, standard deviation, variance, percentiles, skewness, kurtosis, median | Yes | Yes |
| SummaryStatistics | min, max, mean, geometric mean, n, sum, sum of squares, standard deviation, variance | No | No |
MultivariateSummaryStatistics 与 SummaryStatistics 相似,适用于多元数据,也可以用来计算输入数据的全协方差矩阵。
DescriptiveStatistics 和 SummaryStatistics 都是非线程安全类,在多线程环境中,需要使用 SynchronizedDescriptiveStatistics ,SynchronizedSummaryStatistics,SynchronizedMultivariateSummaryStatistics。
StatUtils 是一个工具类,提供了很多静态方法,用来计算 doulbe[] 数组的特定统计值。
使用 DescriptiveStatistics 示例:
// Get a DescriptiveStatistics instance
DescriptiveStatistics stats = new DescriptiveStatistics();// Add the data from the array
for( int i = 0; i < inputArray.length; i++) {stats.addValue(inputArray[i]);
}// Compute some statistics
double mean = stats.getMean();
double std = stats.getStandardDeviation();
double median = stats.getPercentile(50);
使用 StatUtils 示例:
// Compute statistics directly from the array
// assume values is a double[] array
double mean = StatUtils.mean(values);
double std = FastMath.sqrt(StatUtils.variance(values));
double median = StatUtils.percentile(values, 50);// Compute the mean of the first three values in the array
mean = StatUtils.mean(values, 0, 3);
Rolling Mean 窗口(Window):为提高数据的准确性,将某个点的取值扩大到包含这个点的一段区间,这个区间就是窗口。
double[] data = {0,1,2,3,4,5,6,7,8,9,10};double[] rollingMean = new double[data.length]; // 0.0, 0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5,9.5DescriptiveStatistics stats = new DescriptiveStatistics();stats.setWindowSize(2);for (int i = 0; i < data.length; i++) {stats.addValue(data[i]);rollingMean[i] = stats.getMean();}
3、Frequency distributions:频率分布
Frequency 提供了一组计算离散数据统计量与百分比的接口。离散数据的类型,可以是 String, integer, long, char,以及任何实现了 Comparable 接口的其他类。
计算整数值的频率分布:
Frequency f = new Frequency();f.addValue(1);f.addValue(new Integer(1));f.addValue(new Long(1));f.addValue(2);f.addValue(new Integer(-1));System.out.prinltn(f.getCount(1)); // 数值 1 出现的次数:3System.out.println(f.getCumPct(0)); // < 0 的数值的累积百分比:0.2System.out.println(f.getPct(new Integer(1))); // 1 的百分比 0.6System.out.println(f.getCumPct(-2)); // < -2 的数值的累积百分比 0System.out.println(f.getCumPct(10)); // < 10 的数值的累积百分比 1
4、Simple regression : 简单回归
Simple regression 属于一元线性回归模型: y = intercept + slope * x or y = slope * x,
一元线性回归是分析只有一个自变量(自变量x和因变量y)线性相关关系的方法
建立模型
1、选取一元线性回归模型的变量 ;
2、绘制计算表和拟合散点图 ;
3、计算变量间的回归系数及其相关的显著性 ;
4、回归分析结果的应用 [2] 。
模型的检验
1、经济意义检验:就是根据模型中各个参数的经济含义,分析各参数的值是否与分析对象的经济含义相符;
2、回归标准差检验;
3、拟合优度检验;
4、回归系数的显著性检验。
有关一元线性回归的详细说明可以参考 :
https://blog.csdn.net/chaoping315/article/details/81463544
https://blog.csdn.net/antony1776/article/details/98846299
观察点 (x, y) 数值序列可以逐个添加,或者以二维数组的形式添加。
SimpleRegression regression = new SimpleRegression();regression.addData(1d, 2d);regression.addData(3d, 3d);regression.addData(3d, 3.3d);regression.addData(4d, 5d);System.out.println(regression.getIntercept()); // 0.8210526315789481System.out.println(regression.getSlope()); // 0.9105263157894735System.out.println(regression.getSlopeStdErr()); // 0.27710413854922505System.out.println(regression.predict(8)); // 8.105263157894736
5、Multiple linear regression:多元线性回归
OLSMultipleLinearRegression 和 GLSMultipleLinearRegression 使用最小二乘法来拟合多元回归模型:
1.普通最小二乘法
普通最小二乘法(Ordinary Least Square, OLS)通过最小化误差的平方和寻找最佳函数。通过矩阵运算求解系数矩阵:
OLS regression
OLSMultipleLinearRegression regression = new OLSMultipleLinearRegression();
double[] y = new double[]{11.0, 12.0, 13.0, 14.0, 15.0, 16.0};
double[][] x = new double[6][];
x[0] = new double[]{0, 0, 0, 0, 0};
x[1] = new double[]{2.0, 0, 0, 0, 0};
x[2] = new double[]{0, 3.0, 0, 0, 0};
x[3] = new double[]{0, 0, 4.0, 0, 0};
x[4] = new double[]{0, 0, 0, 5.0, 0};
x[5] = new double[]{0, 0, 0, 0, 6.0};
regression.newSampleData(y, x);double[] beta = regression.estimateRegressionParameters();
double[] residuals = regression.estimateResiduals();
double[][] parametersVariance = regression.estimateRegressionParametersVariance();
double regressandVariance = regression.estimateRegressandVariance();
double rSquared = regression.calculateRSquared();
double sigma = regression.estimateRegressionStandardError();
通过模拟数据来验证 OLS 回归算法:
OLSMultipleLinearRegression regression = new OLSMultipleLinearRegression();double[] y = new double[100];double[] beta = new double[] {2, 5, 16, 9, -3, -5, -2};double[][] X = new double[100][beta.length];Random random = new Random();for (int i = 0; i < 100; i++) {for (int j = 0; j < beta.length; j++) {X[i][j] = random.nextGaussian();}}for (int i = 0; i < 100; i++) {y[i] = 0;for (int j = 0; j < beta.length; j++) {y[i] += X[i][j]*beta[j];}y[i] += random.nextGaussian();}regression.newSampleData(y, X);double[] _beta = regression.estimateRegressionParameters();for (int i = 0; i < beta.length; i++) {System.out.println(String.format("%d : 实际值 = %s , 预测值 = %s", i, beta[i], _beta[i+1]));}}
输出结果为:
2.广义最小二乘法
广义最小二乘法(Generalized Least Square)是普通最小二乘法的拓展,它允许在误差项存在异方差或自相关,或二者皆有时获得有效的系数估计值。公式:
其中,Ω是残差项的协方差矩阵。
GLS regression
GLSMultipleLinearRegression regression = new GLSMultipleLinearRegression();
double[] y = new double[]{11.0, 12.0, 13.0, 14.0, 15.0, 16.0};
double[][] x = new double[6][];
x[0] = new double[]{0, 0, 0, 0, 0};
x[1] = new double[]{2.0, 0, 0, 0, 0};
x[2] = new double[]{0, 3.0, 0, 0, 0};
x[3] = new double[]{0, 0, 4.0, 0, 0};
x[4] = new double[]{0, 0, 0, 5.0, 0};
x[5] = new double[]{0, 0, 0, 0, 6.0};
double[][] omega = new double[6][];
omega[0] = new double[]{1.1, 0, 0, 0, 0, 0};
omega[1] = new double[]{0, 2.2, 0, 0, 0, 0};
omega[2] = new double[]{0, 0, 3.3, 0, 0, 0};
omega[3] = new double[]{0, 0, 0, 4.4, 0, 0};
omega[4] = new double[]{0, 0, 0, 0, 5.5, 0};
omega[5] = new double[]{0, 0, 0, 0, 0, 6.6};
regression.newSampleData(y, x, omega);
6、Rank transformations :
7、Covariance and correlation: 协方差和相关性
org.apache.commons.math4.stat.correlation 包中的类可用于计算数组或矩阵的协方差和相关性;
Covariance:协方差SpearmansCorrelation: 斯皮尔曼等级相关KendallsCorrelation:肯德尔相关性
三个相关性系数(pearson, spearman, kendall)反应的都是两个变量之间变化趋势的方向以及程度,其值范围为-1到+1,0表示两个变量不相关,正值表示正相关,负值表示负相关,值越大表示相关性越强。
PearsonsCorrelation : 皮尔逊相关
两个变量(X, Y)的皮尔森相关性系数(ρX,Y)等于它们之间的协方差cov(X,Y)除以它们各自标准差的乘积(σX, σY)。
公式的分母是变量的标准差,这就意味着计算皮尔森相关性系数时,变量的标准差不能为0(分母不能为0),也就是说你的两个变量中任何一个的值不能都是相同的(不能是一条直线)。如果没有变化,用皮尔森相关系数是没办法算出这个变量与另一个变量之间是不是有相关性的。
PearsonsCorrelation pearsonsCorrelation = new PearsonsCorrelation();double[] x = {1,2,3,4,5,6,7};double[] y = {1.1, 2.2, 3.1, 4.0, 5.1, 6.2, 7};double[] y1 = {1, 1, 1, 1, 1, 1, 1};System.out.println(pearsonsCorrelation.correlation(x, y)); // 0.9993294815748658System.out.println(pearsonsCorrelation.correlation(x, y1)); // NaNCovariance covariance = new Covariance();double cov = covariance.covariance(x, y); // x,y 的 协方差double xd = Math.sqrt(StatUtils.variance(x)); // x 的标准差double yd = Math.sqrt(StatUtils.variance(y)); // y 的标准差System.out.println(cov/(xd*yd)); // 0.9993294815748657
也可以通过 R 方来求解皮尔逊相关性系数:
y ^ i \hat{y}_i y^i 为根据 x i x_i xi 预测的 y 值, y i y_i yi 为实际值, y i − y ^ i y_i - \hat{y}_i yi−y^i 为残差。 y ˜ \text{\~{y}} y˜ 为 y 数列的均值。
@Testpublic void simpleTest() {SimpleRegression regression = new SimpleRegression();PearsonsCorrelation pearsonsCorrelation = new PearsonsCorrelation();double[] x = {1,2,3,4,5,6,7};double[] y = {1.1, 2.2, 3.1, 4.0, 5.1, 6.2, 7};for (int i = 0; i < x.length; i++) {regression.addData(x[i], y[i]);}double regressionSumSquares = 0d;double totalSumSquares = 0d;double meanY = StatUtils.mean(y);for (int i = 0; i < y.length; i++) {double a = regression.predict(x[i])-meanY;double c = y[i] - meanY;regressionSumSquares += a*a;totalSumSquares += c*c;}double rSquare = regressionSumSquares/totalSumSquares;System.out.println(String.format("TotalSumSquares = %s", totalSumSquares));System.out.println(String.format("RegSumSquares = %s", regressionSumSquares));System.out.println(Math.sqrt(rSquare));System.out.println(pearsonsCorrelation.correlation(x, y));}
SpearmanCorrelation : 斯皮尔曼相关性
斯皮尔曼相关性系数,通常也叫斯皮尔曼秩相关系数。“秩”,可以理解成就是一种顺序或者排序,那么它就是根据原始数据的排序位置进行求解,这种表征形式就没有了求皮尔森相关性系数时那些限制。下面来看一下它的计算公式:
计算过程就是:首先对两个变量(X, Y)的数据进行排序,然后记下排序以后的位置(X’, Y’),(X’, Y’)的值就称为秩次,秩次的差值就是上面公式中的di,n就是变量中数据的个数,最后带入公式就可求解结果。举个例子吧,假设我们实验的数据如下:
带入公式,求得斯皮尔曼相关性系数:ρs= 1-6*(1+1+1+9)/6*35=0.657
参考: http://blog.sina.com.cn/s/blog_69e75efd0102wmd2.html
8、Statistical tests : 统计检验
org.apache.commons.math4.stat.inference 包中提供了各种统计检验先关的实现,如 :
Student’s t, Chi-Square, G Test, One-Way ANOVA, Mann-Whitney U, Wilcoxon signed rank and Binomial test statistics as well as p-values associated with t-, Chi-Square, G, One-Way ANOVA, Mann-Whitney U Wilcoxon signed rank, and Kolmogorov-Smirnov tests.
相应的类有 TTest, ChiSquareTest, GTest, OneWayAnova, MannWhitneyUTest, WilcoxonSignedRankTest, BinomialTest, KolmogorovSmirnovTest