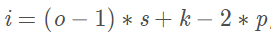前言

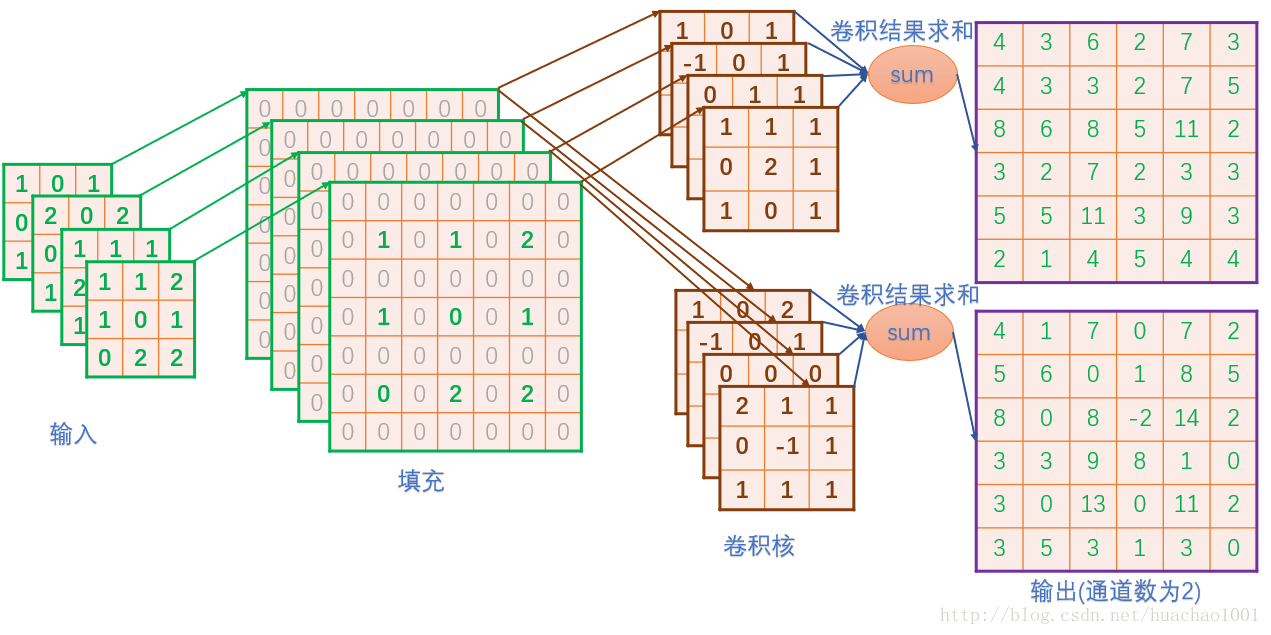
一维反卷积(deconv)，可以很好的实现一维卷积的反过程！但是二维反卷积就很难恢复了！为什么呢？因为我们知道二维卷积计算的过程就是：卷积核不断滑动，卷积核不断与原始数据中的小矩阵做"点乘并求和"；现假设卷积核为3x3，那么每一个和它点乘的小矩阵对应尺寸也是3x3。现在我们只知道"卷积核里的9个数"和这两个小矩阵"卷积操作后"的"一个"数值结果！也就说是"小矩阵里的9个元素"都还是"未知的"！这个方程没办法解的，也就没办法恢复原矩阵的。

网上关于二维反卷积实现的方法

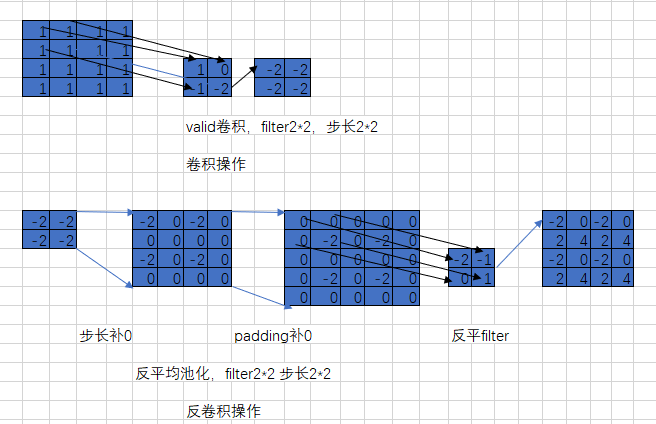
这里的二维反卷积更像是一种别的操作，它已经不符合"(一维)卷积与反卷积的定义了！所以这种操作的"实际意义也还不明确"(Matlab中也没有自带的相关命令)。本文纯粹是把其方法实现，不深究其结果和意义。

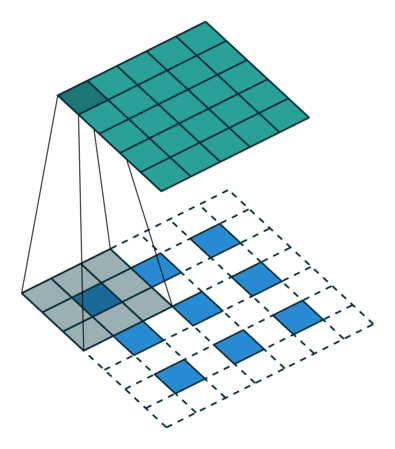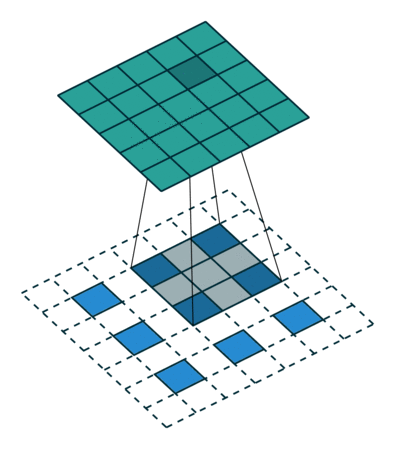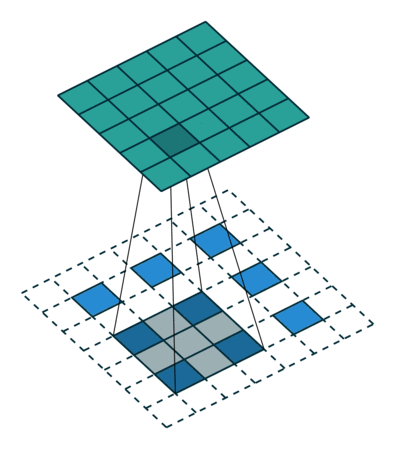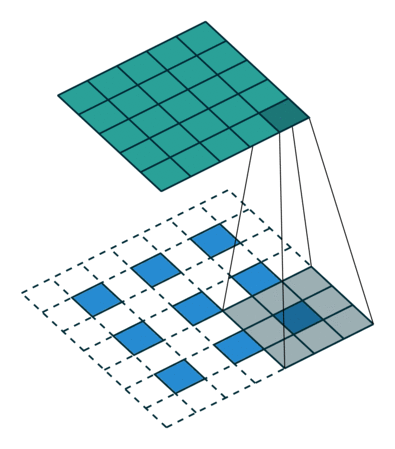
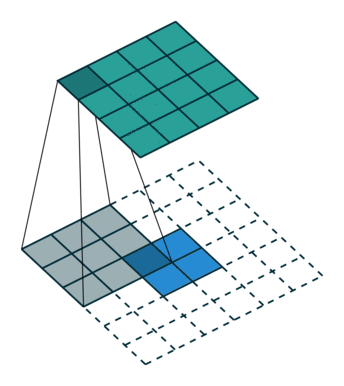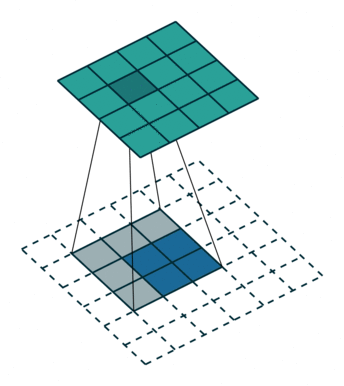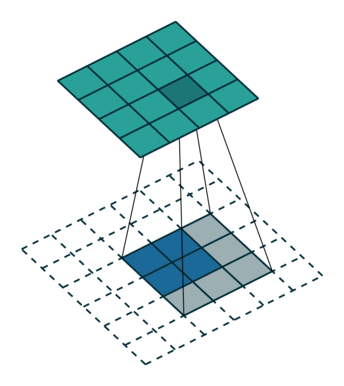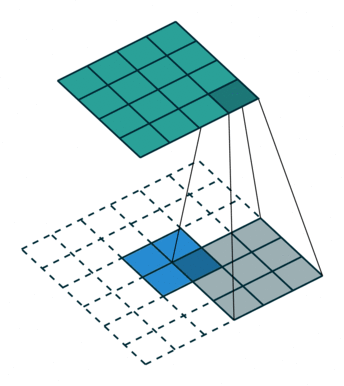
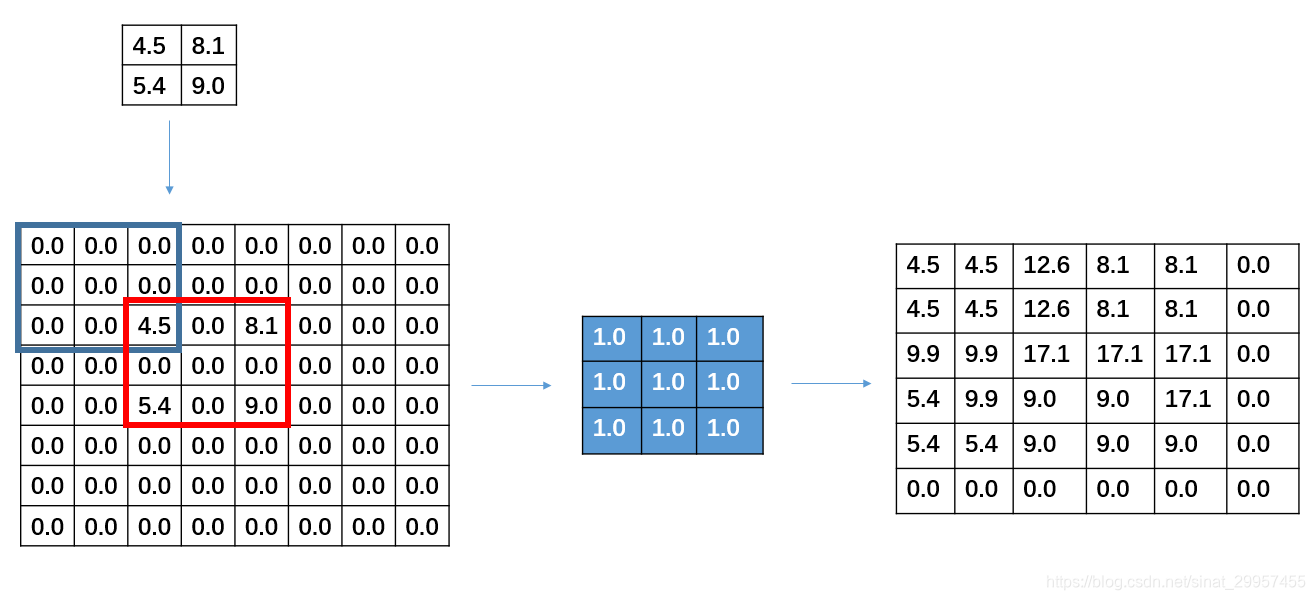
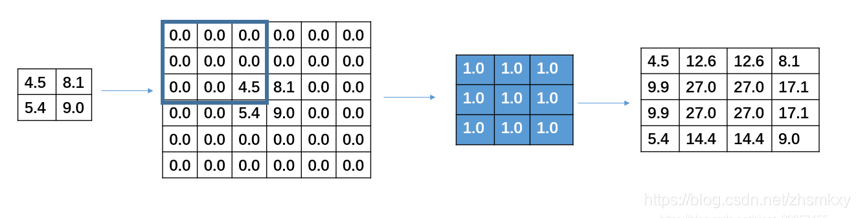
首先二维反卷积的输入是"二维卷积处理后的图像矩阵"，卷积核还是"原先的卷积核"。二维反卷积分两步：1. 预处理：卷积核翻转180°，原始图像矩阵每个元素扩0边，操作如图1所示；2. 卷积计算，操作如这里所示。

图1：预处理操作

Matlab编程实现

可以看出二维反卷积操作其实非常简单，其对应的处理一张二维图片矩阵的操作如下(这里是对3通道的彩图处理的)：

clc; clear;

% 卷积核

<