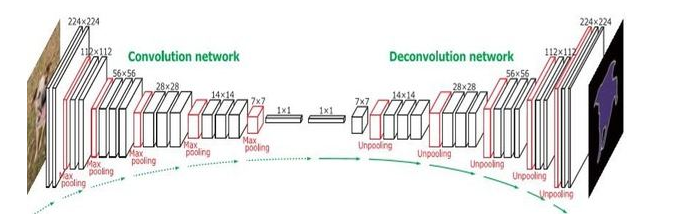
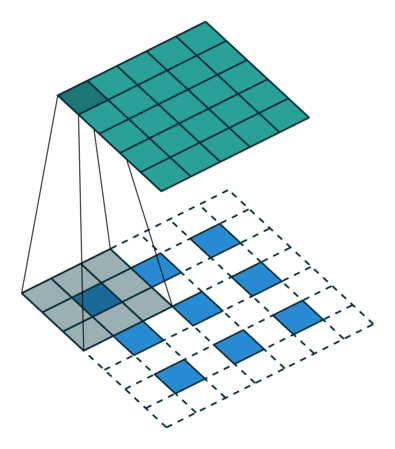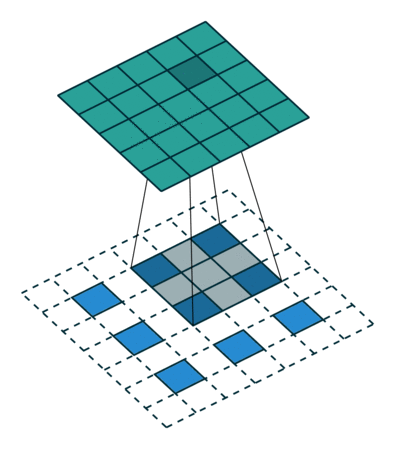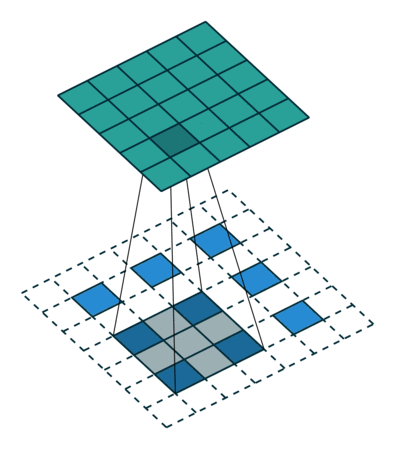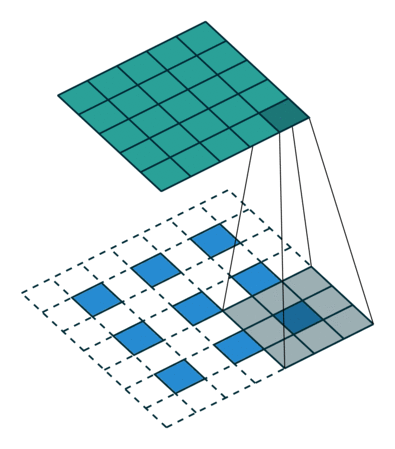
前言

本篇将详细地讲解地震信号中用到的反卷积方法。反卷积方法的作用在文章 地震信号的一些基本概念 中已经阐述过，简单的说就是：在压缩原信号的同时，对频谱进行补偿（反卷积的输出信号）。而在地震信号处理中，除了前面的优势，该方法还可以使反射系数成为尖脉冲，从而提高地震记录的分辨率。

地震记录：就是由仪器在地表所测的地震数据
反射系数：表征的是地球的每一层对地震波的反射特征，相当于一个系统或是滤波器，可看作为滤波器系数
地震记录的分辨率：地震记录的目的是想把地球的每一层进行区分和识别，而区分的细度就是所谓的分辨率，所能识别的底层越多，则分辨率越高，反之越低。

地震记录定义（输出信号）

我们首先给出地震记录的定义：
$$x\left(t\right)=s\left(t\right)\ast \epsilon \left(t\right)$$
其中
$x\left(t\right)$：地震记录，$s\left(t\right)$：地震子波， $\epsilon \left(t\right)$：反射系数序列

地震子波包括震源子波，记录滤波器，地表反射和检波器的组合响应。上述定义省去了噪音的影响。

地震子波：与相关子波（相关序列）是不同的概念，它不是相关序列

反卷积要处理的问题

在地震勘探中，当地下层位较密集时，它们之间的反射层将难以区分，见下图：

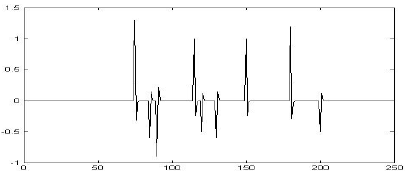
前三个反射层间距很接近。

所以希望反射层的反射系数为一系列的尖脉冲，这样就能从地震记录中把各反射层区分开来，从而提高了地震记录的分辨率。如何将非尖脉冲的信号压缩成尖脉冲的反射系数，就是反卷积要处理的问题和重点。

反卷积方法

首先我们使用地震记录定义
$x\left(t\right)=s\left(t\right)\ast \epsilon \left(t\right)$
对其进行时域到频域的变换（傅里叶变换），得到
$x\left(\omega \right)=s\left(\omega \right)E\left(\omega \right)$
其中
$x\left(\omega \right)$ 为地震记录 $x\left(t\right)$ 的频谱；
$s\left(t\right)$ 为地震子波 $s\left(\omega \right)$ 的频谱；
$E\left(\omega \right)$ 为反射系数的频谱；
显然，
$E\left(\omega \right)=\frac{x\left(\omega \right)}{s\left(\omega \right)}$,
令
$A\left(\omega \right)=\frac{1}{s\left(\omega \right)}$,
则
$E\left(\omega \right)=A\left(\omega \right)x\left(\omega \right)$
转到时域为：
$\epsilon \left(t\right)=a\left(t\right)\ast x\left(t\right)=a\left(t\right)\ast s\left(t\right)\ast \epsilon \left(t\right)$
其中
$a\left(t\right)$ 是 $A\left(\omega \right)$ 的时域序列。

根据上式和卷积的同元性质可知：
$a\left(t\right)\ast s\left(t\right)=\delta \left(t\right)$ （1）

其中
$\delta \left(t\right)=\{\begin{array}{l}0,t\ne 0\\ 1,t=0\end{array}$

而 $a\left(t\right)$ 地震反子波。

根据已知地震子波 $s\left(t\right)$，即可求出地震反子波 $a\left(t\right)$ ，而根据卷积模型
$$\begin{gathered} E\left(\omega \right)=A\left(\omega \right)x\left(\omega \right) \\ \Rightarrow \epsilon \left(t\right)=a\left(t\right)\ast x\left(t\right) \end{gathered}$$
就可求出反射系数 $\epsilon \left(t\right)$。
上述过程是反卷积的全过程，特别地，它是反卷积的一个特例，即反滤波，所谓反滤波是因为滤波算子 $a\left(t\right)$ 是地震子波的逆。

地震子波最小相位的假设：由于在求取反卷积滤波算子时，地震子波的频谱作为分母出现，很明显为了使反滤波算子稳定，地震子波必须是最小相位的，因为最小相位的零点都位于单位圆内，也就是作为分母出现的极点

扩展知识

上一节的过程看似顺理成章，其实隐含了一个最优方法求解滤波算子的过程。我们从最初的地震记录卷积模型得到：
$x\left(t\right)\ast f\left(t\right)=s\left(t\right)\ast f\left(t\right)\ast \epsilon \left(t\right)$
当 $s\left(t\right)\ast f\left(t\right)=\delta \left(t\right)$ 时，即为上一节的式（1）。
其实 $\delta \left(t\right)$ 是一个期望输出，而实际输出为 $s\left(t\right)\ast f\left(t\right)$，那么使用最小二乘原理的目标误差函数为
$e\left(t\right)=\sum {\left(s\left(t\right)\ast f\left(t\right)-\delta \left(t\right)\right)}^2$
所以最理想的情况就是误差函数为0，即 $s\left(t\right)\ast f\left(t\right)=\delta \left(t\right)$。
此外，为了反射系数达到更好的波形，我们可以选择俞式子波作为期望输出（该知识也超出本篇范围）。

小结

本篇既是地震信号补偿频谱的基础也是对提高反射坡面识别率的重要基础，地震信号的处理技术很多都基于反卷积知识，当然还有最小相位，混合相位和最大相位的区分，还有期望输出子波的选择等等，它们都是以此为基础来对地震信号进行处理的。
（如有错误，请指正）