1、卷积

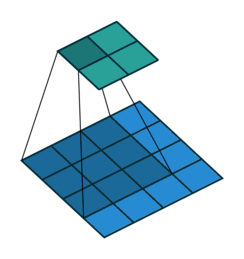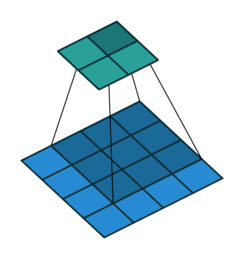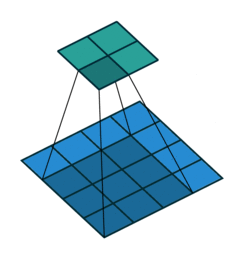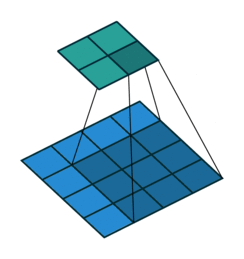
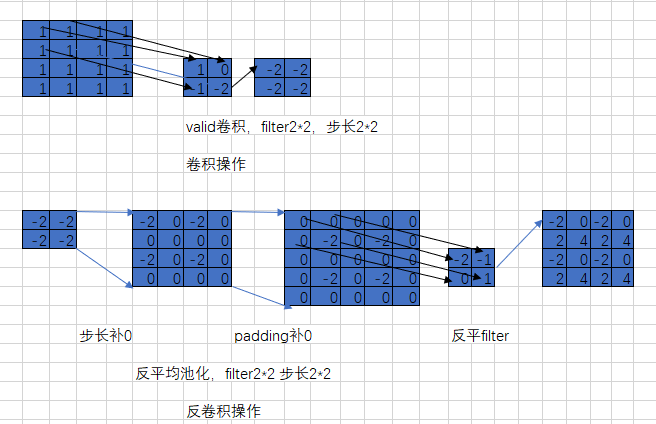
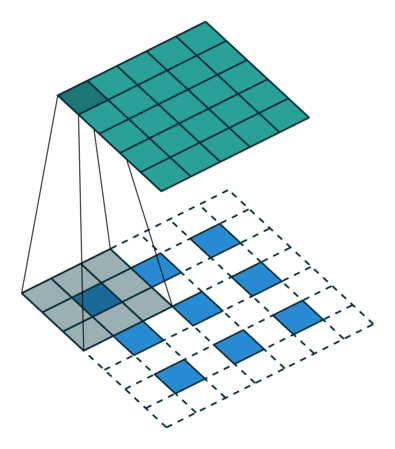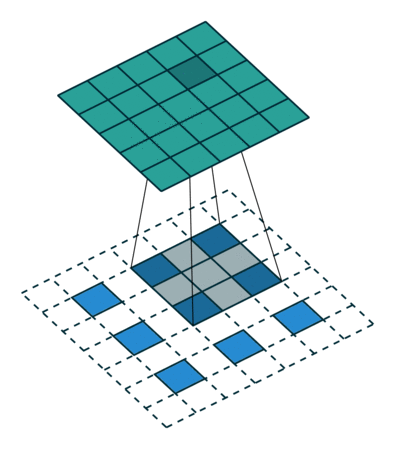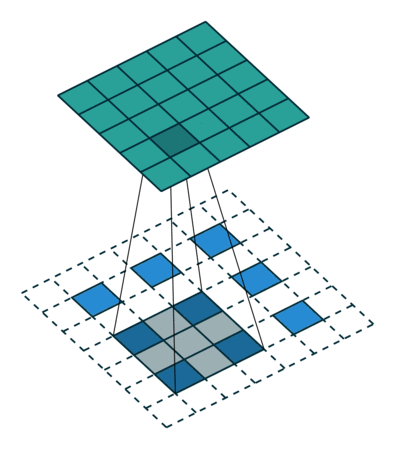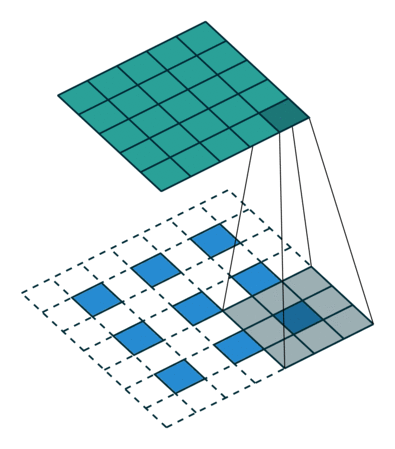
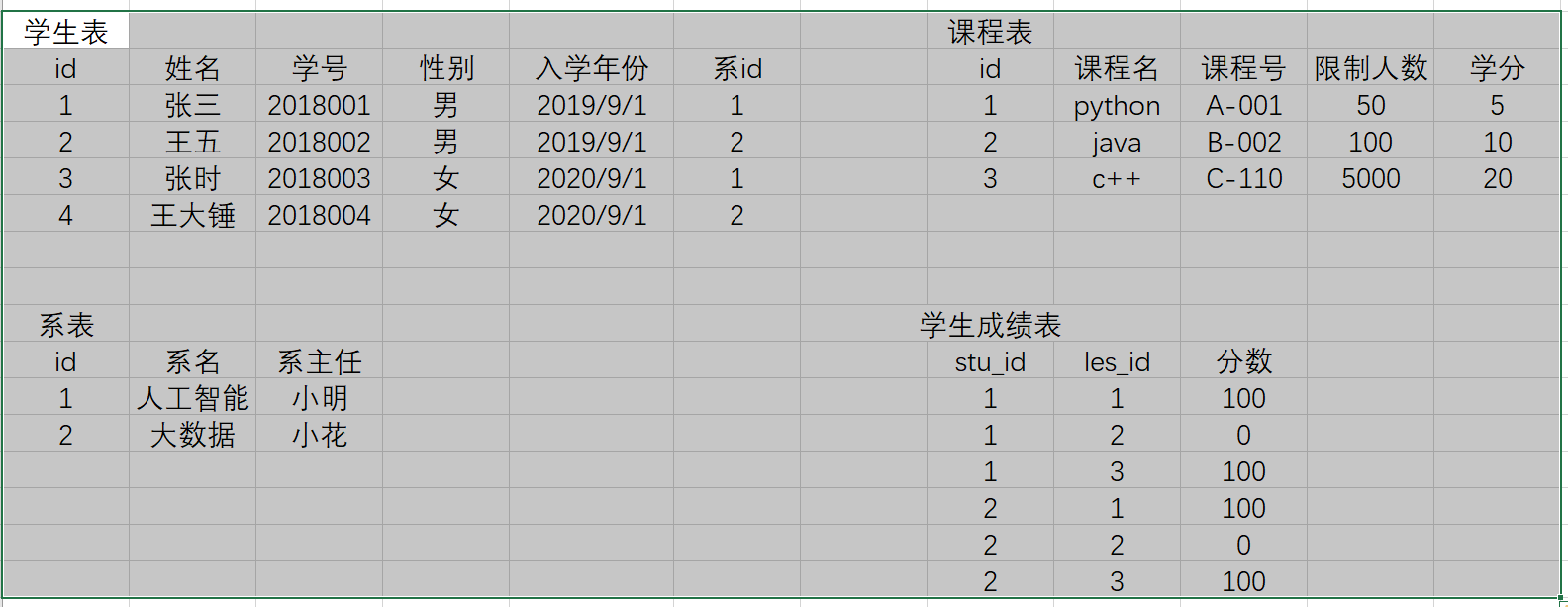
上图展示了一个卷积的过程，其中蓝色的图片(4*4)表示的是进行卷积的图片，阴影的图片(3*3)表示的是卷积核，绿色的图片(2*2)表示是进行卷积计算之后的图片。在卷积操作中有几个比较重要的参数，输入图片的尺寸、步长、卷积核的大小、输出图片的尺寸、填充大小。

 

2、卷积参数介绍

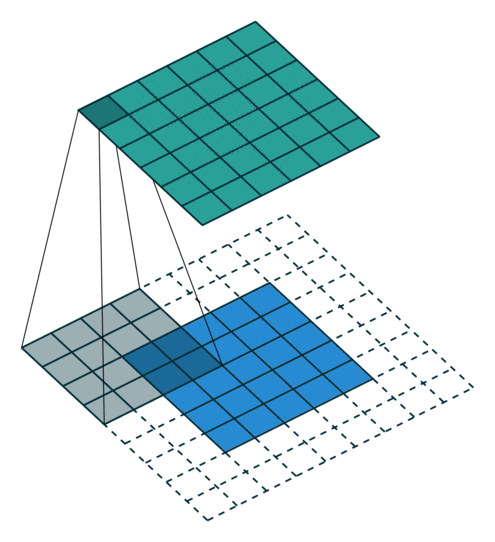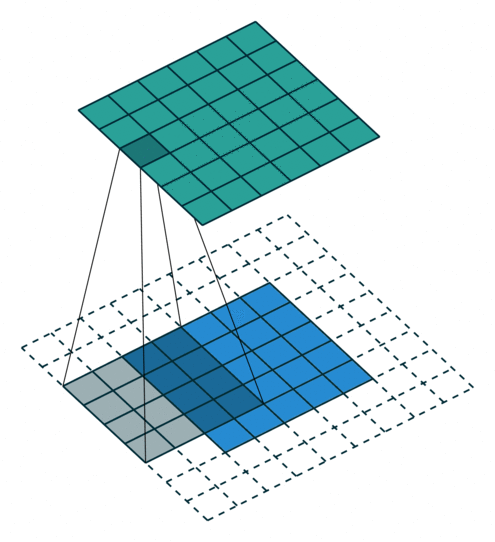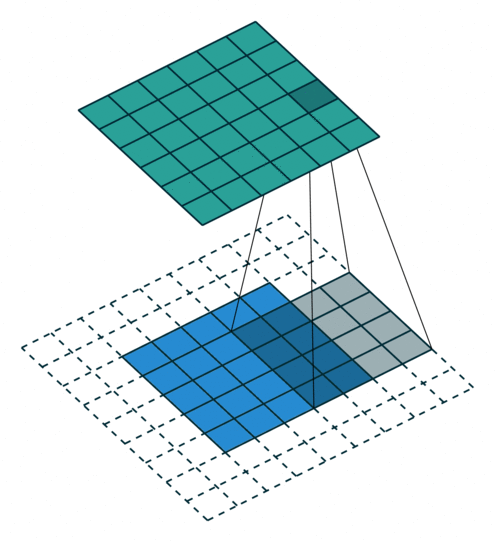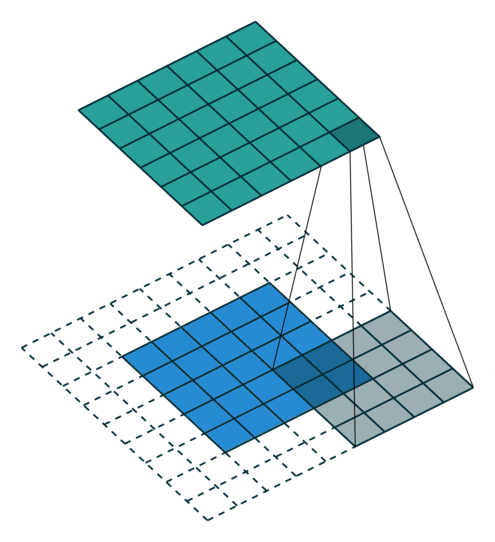
输入图片的尺寸：上图中的蓝色图片(4*4)，表示的是需要进行卷积操作的图片，在后面的公式中用 i 来表示输入图片的尺寸。

卷积核的大小：上图中的会移动阴影图片表示的是卷积核(3*3)，通过不同参数不同大小的卷积核可以提取到图片的不同特征，后面用 k 表示卷积核的尺寸。

步长：是指卷积核移动的长度，通过上图可以发现卷积核水平方向移动的步长和垂直方向移动的步长是一样的都是1，后面用 s 表示步长。

填充大小：是指在输入图片周围填充的圈数，通常都是用0来进行填充的，上图中蓝色图片周围两圈虚线的矩形表示的是填充的值，所以填充掉是2，后面用p来表示填充大小。

输出图片的尺寸：经过卷积操作之后获取到的图片的大小，上图的绿色图片(6*6)，后面用o来表示。

 

3、反卷积

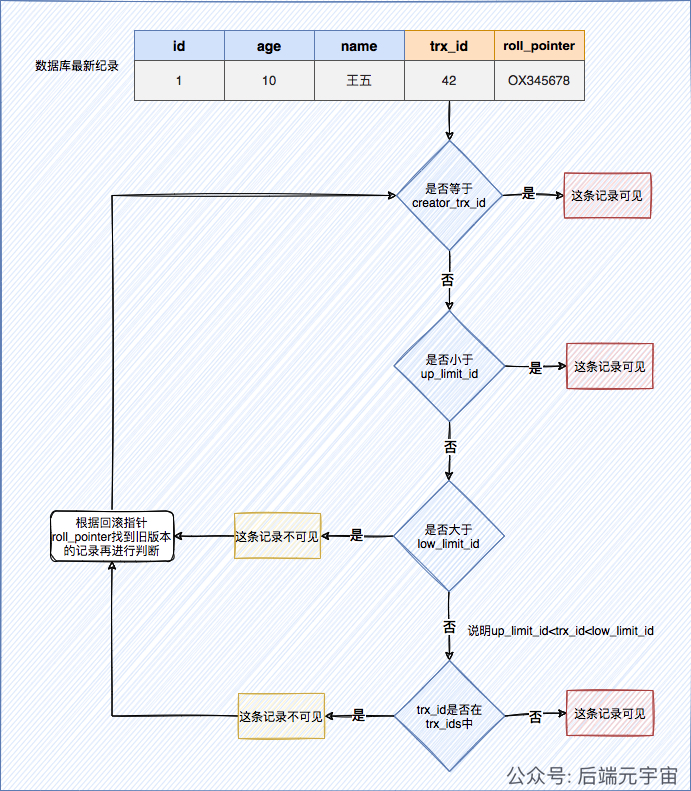
反卷积也被称为转置卷积，反卷积其实就是卷积的逆过程。大家可能对于反卷积的认识有一个误区，以为通过反卷积就可以获取到经过卷积之前的图片，实际上通过反卷积操作并不能还原出卷积之前的图片，只能还原出卷积之前图片的尺寸。那么到底反卷积有什么作用呢？通过反卷积可以用来可视化卷积的过程，反卷积在GAN等领域中有着大量的应用。

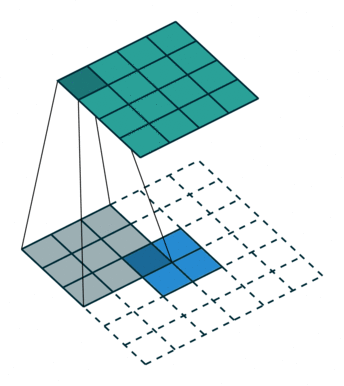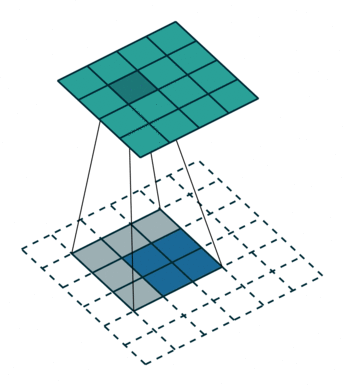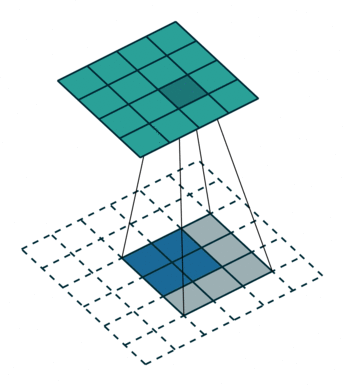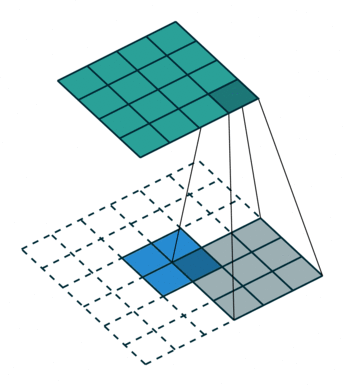
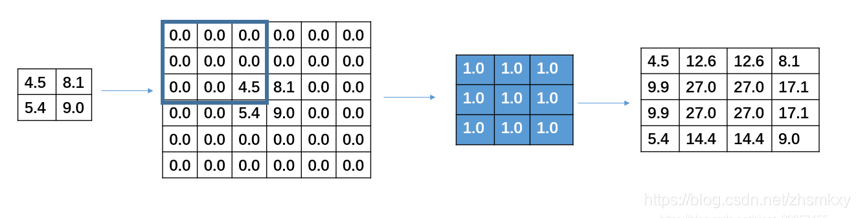
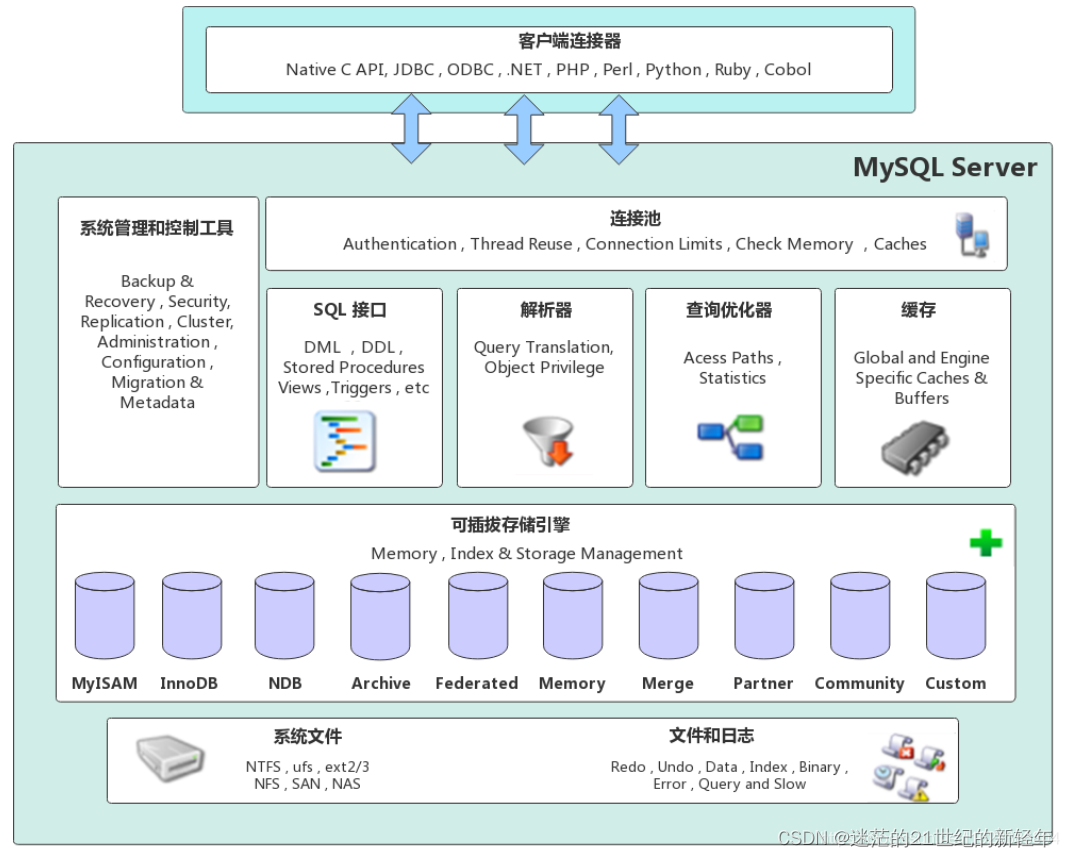
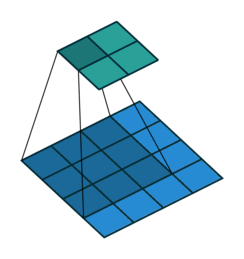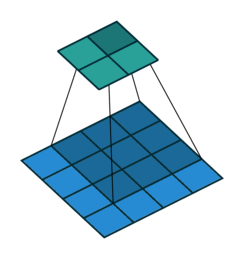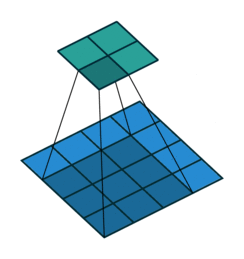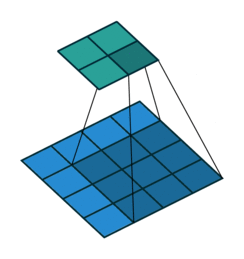
上图展示一个反卷积的工作过程，乍看一下好像反卷积和卷积的工作过程差不多，主要的区别在于反卷积输出图片的尺寸会大于输入图片的尺寸，通常通过增加padding来实现这一操作，上图展示的是一个strides(步长)为1的反卷积。下面看一个strides不为1的反卷积。

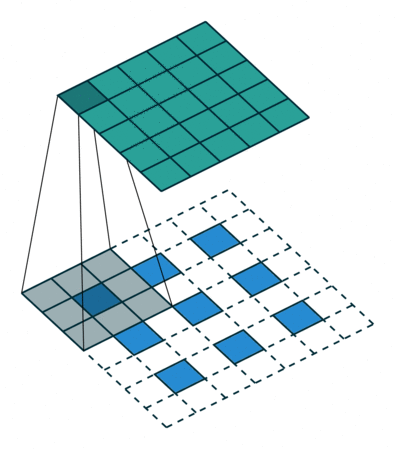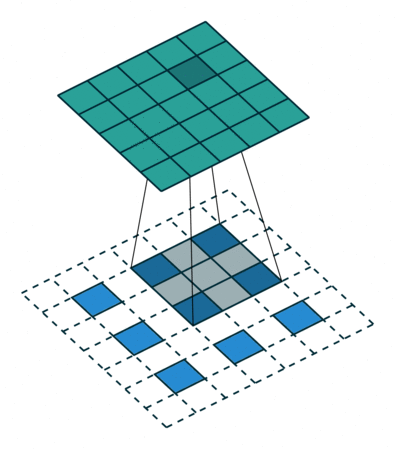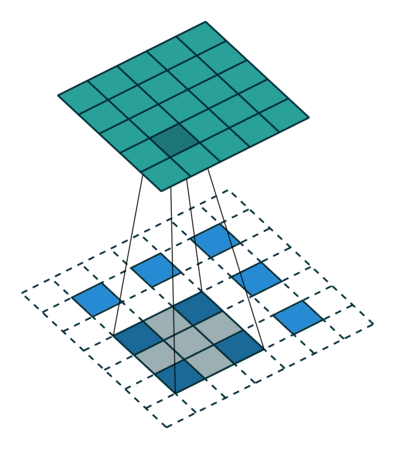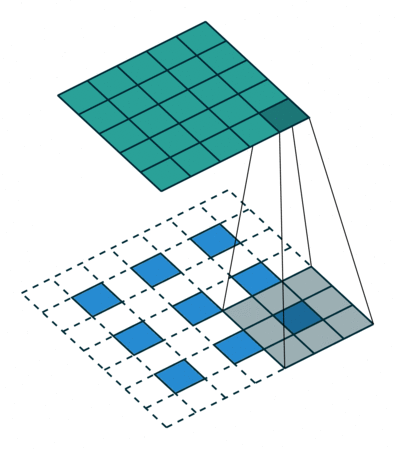
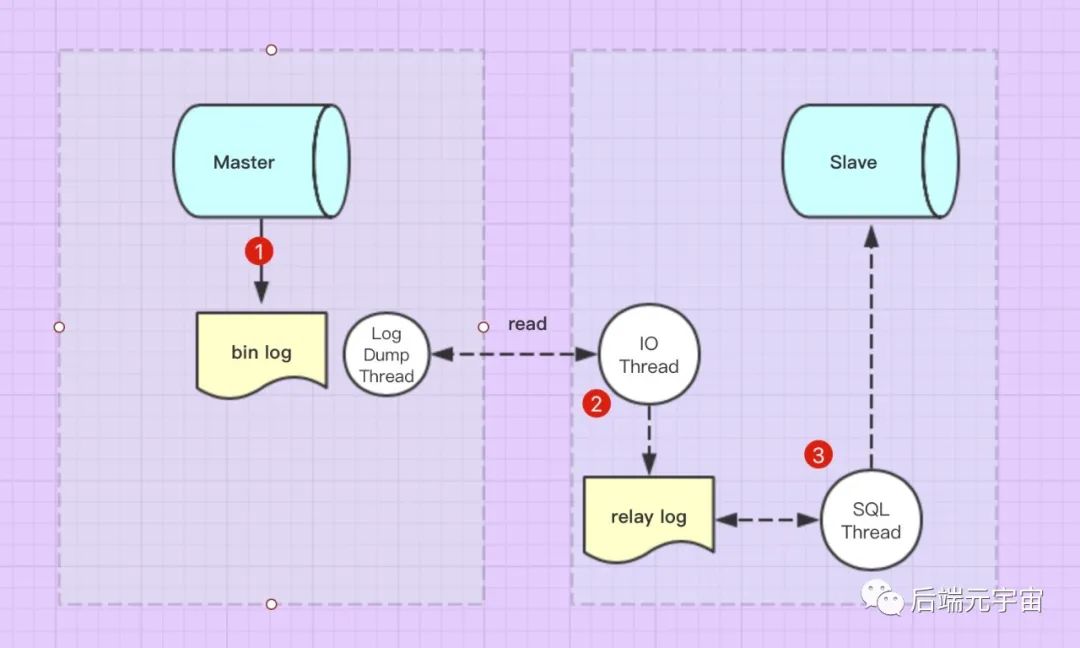
上图中的反卷积的stride为2，通过间隔插入padding来实现的。

 

4、卷积模式

TensorFlow提供的卷积函数padding只有"SAME"和"VALID"两种模式，所以输出矩阵的尺寸大小与之前的公式有所不同，下面介绍这两种模式下输出矩阵尺寸的计算公式：

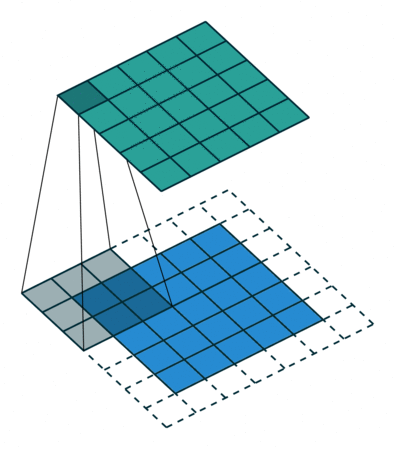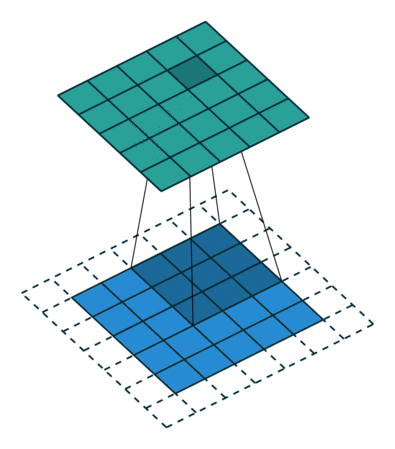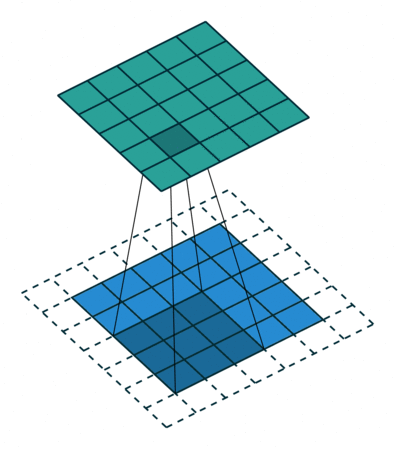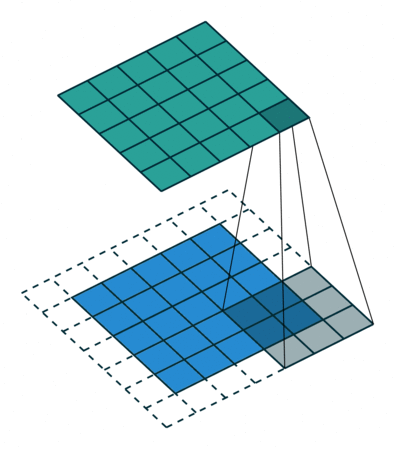
padding为SAME时：ceil(i/s)，其中i表示输入矩阵的大小，s表示卷积核的步长，ceil函数表示向上取整。下图展示是一个padding为SAME的卷积，卷积开始的时候保证卷积核的中心位于输入矩阵角的顶点位置。

padding为VALID时：，k表示卷积核的尺寸。下图展示的是一个padding为VALID的卷积过程，卷积核始终都是位于输入矩阵内进行移动。

 

5、卷积后图像大小计算

如果已知 i、k、p、s，可以求得o，

卷积计算公式如下：

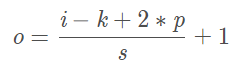
同样，可以根据反卷积的o、s、k、参数来计算反卷积的输出 i，也就是卷积的输入。

反卷积公式如下：

，其实就是根据上式推导出来的。