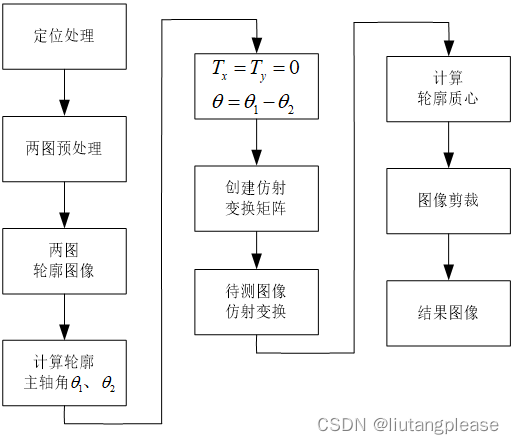
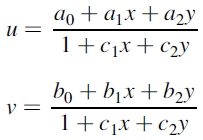图像配准在医学图像领域是一项重要的技术，在许多的临床诊断中，为了分析患者的状况，常常需要采集患者的扫描影像，例如，X线、MRI、CT和超声，这些扫描影像可以对患者的诊断提供依据，然而，在独立的影像中，临床信息并不是十分明显，所以采用单模或者多模的方法用以获得额外的临床信息，出于此目的，发现这些影像间的空间关系就变得很重要。图像配准就是找到一幅图像像素到另一幅图像像素间的空间映射关系。

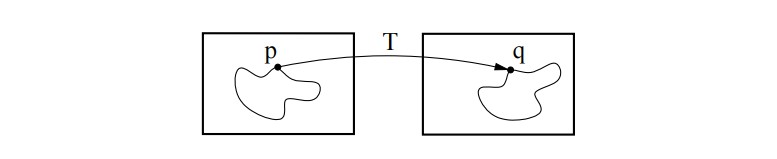
配准过程需要两幅图像，一幅图像（moving image）$ I_M(x) $ 形变到另一幅图像（fixed image）$ I_F(x) $ ，并且这两幅图像都是在各自的空间域上定义且具有相同的维度$ d $，配准就是要找到位移$ u(x) $使得$ I_M(x+u(x)) $ 空间对其到$ I_F(x) $，用一个等价的公式表达就是找到一个变换$ T(x)=x+u(x) $ 使得$ I_M(T(x))$ 空间对其到 $ I_F(x)$，这个变换定义为从$ fixed image $ 到 $ moving image $ 的映射

$ T:\Omega_F \subset \Bbb R^d \to \Omega_M \subset \Bbb R^d $ 对齐的质量通过距离或者相似性测度 $ S$定义，例如平方差和（$ SSD$）、相关比率、互信息（$ MI$），由于这个问题不适用于非刚性变换$ T$，通常引入正则化或惩罚系数 $ \mathcal P$ 来约束$ T$
一般来讲，配准问题是一个使得代价函数 $ \mathcal C $ 最小的优化问题，用公式表达$ T$：
$$\hat{T}=\arg \underset{T}{\min }\mathcal{C}(\mathbf{T};T_F,I_M)$$
$$\mathcal{C}(\mathbf{T};T_F,I_M)=-\mathcal{S}(\mathbf{T};I_F,I_M)+\gamma \mathcal{P}(\mathbf{T})$$

$ \gamma $ 权重因子 为了解决上述最小化问题，有两个基本的方法：参数化和非参数化，这里不讨论非参数化方法，在参数化方法中，引入变换的参数化模型来约束可能变换的数量，原来的优化问题就变成了：
$$\hat{T}=\arg \underset{T_u}{\min }\mathcal{C}({\mathbf{T}}_{\mathbf{u}};T_F,I_M)$$

下标 $u$ 表示变换已被参数化，向量 $u$ 包含变换参数值，例如：当该变换为2D刚性变换，参数向量 $u$ 包含一个旋转角度和$x$和$y$方向上的位移，所以，等式也可以等价于：
$$\hat{u}=\arg \underset{u}{\min }\mathcal{C}(\mathbf{u};T_F,I_M)$$
通过这个等式，原来的问题就变得简化了，通过优化元素$u$取代了优化变换函数T。

图像

相似性测度

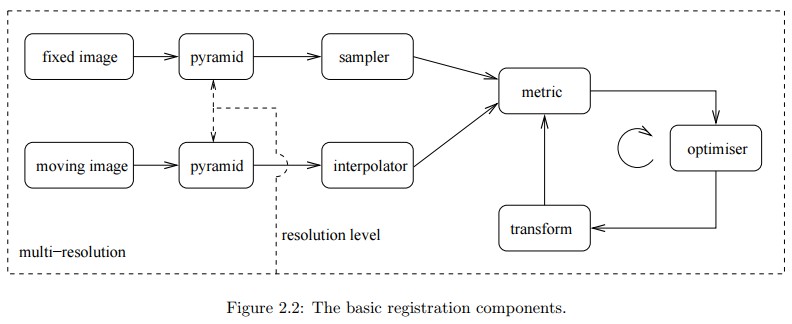
在文献中可以发现相似性测度的几种共同选择，接下来描述几点共同的选择

均方差($ MSD$)：定义

$$MSD(\mu ;I_F,I_M)=\frac{1}{|{\Omega }_F|}\sum _{x_i\in {\Omega }_F}(I_F(x_i)-I_M({\mathbf{T}}_{\mu }(x_i)){)}^2$$

$ \Omega_F $ 为 fixed image 的定义域，$ |\Omega_F| $ 为像素的数量，给定变换$ \boldsymbol T$，这个度量可以通过循环迭代fixed image中的像素来实现

归一化互相关(NCC)

NCC定义为：
$$NCC(\mu ;I_F,I_M)=\frac{{\sum }_{x_i\in {\Omega }_F}(I_F(x_i))-\overline{I_F})(I_M({\mathbf{T}}_{\mu }(x_i))-\overline{I_M})}{\sqrt{{\sum }_{x_i\in {\Omega }_F}(I_F(x_i)-\overline{I_F}{)}^2{\sum }_{x_i\in {\Omega }_F}(I_M({\mathbf{T}}_{\mu }(x_i))-\overline{I_M}{)}^2}}$$