矩阵的初等变换这个概念可能在很多人听来有些陌生,但其实我们早在初中的解多元方程组的时候就用过它。只不过在课本当中,这种方法叫做消元法。我们先来看一个课本里的例子:
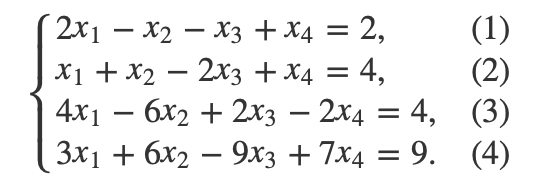
假设我们要解这个方程,怎么做呢?
首先,我们把(1)式加到(2)式,把(4)式加到(3)式,把(1)式乘6加到(4)式可以得到:
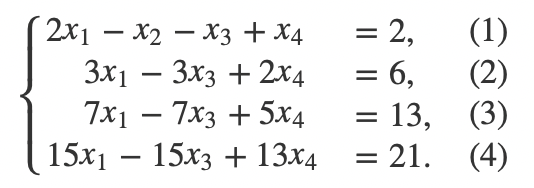
我们再把(4)式减去(2)式乘5,可以解出x4=−3:
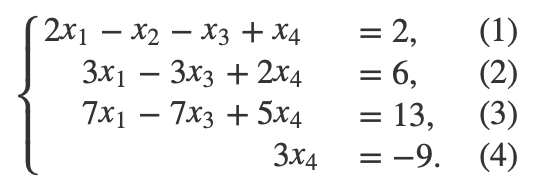
我们把x4=−3带入,可以解出
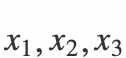 。
。
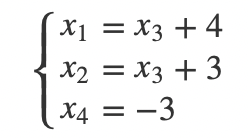
因为消元之后,方程组的数量少于变量的数量,我们无法解出所有的变量。其中的可以取任何值。
上面这个计算的方法我们都非常熟悉,如果我们用一个矩阵来表示所有的次数,那么这个矩阵D可以写成:
那么,我们刚才消元的过程,其实就是对这个矩阵做初等变换。我们把这个过程总结一下,矩阵的初等变换操作包含以下三种:
对调两行
以数k,k≠0乘上某行的所有元素
以数k,k≠0乘上某行所有元素并加到另一行
以上的三种都是针对行为单位的,因此上面的三种变换也称为“行变换”。同样我们也可以对列做如上的三种操作,称为“列变换”。行变换和列变换结合就是矩阵的初等变换。
同样,我们可以对D这个矩阵使用刚才我们上述的初等变换操作,将它变成如下这个结果:
它就对应方程组:
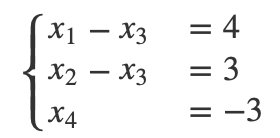
Dt矩阵是经过初等行变换的结果,我们还可以再对它进行列变换,将它变得更简单,我们只要交换第三和第三列,之后就可以通过初等列变换把第五列消除,之后它就变成了下面这个样子:
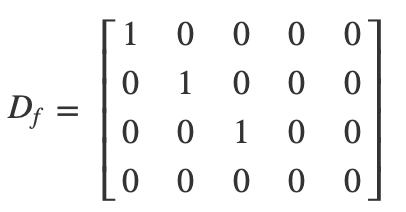
我们用数据归纳法可以很容易证明,所有的m*n的矩阵经过一系列初等变换,都可以变成如下的形式:
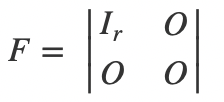
r就是最简矩阵当中非零行的行数,它也被称为矩阵的秩。我们把A矩阵的秩记作: R(A)
之前我们在介绍行列式的时候说过,行列式还存在多种性质。其中之一就是一个矩阵经过初等变换,它的行列式保持不变。我们又知道,如果行列式当中存在某一行或者某一列全部为0,那么它的行列式为0。
所以,我们可以得到,对于n阶矩阵A而言,如果它的秩R(A)
再根据我们前文当中有关可逆矩阵的定义,可以得到,可逆矩阵的秩就等于矩阵的阶数,不可逆矩阵的秩小于矩阵的阶数。所以,可逆矩阵又称为满秩矩阵,不可逆矩阵(奇异矩阵)又称为降秩矩阵。
之前我们在复习行列式以及逆矩阵的时候,总觉得少了些什么,现在有了矩阵的秩的概念之后,这些知识就能串起来了。
代码计算
同样,numpy当中也继承了计算矩阵秩的工具。我们可以很轻松的用一行代码算出矩阵的秩,这样我们在判断矩阵是否可逆的时候,就不需要通过行列式来判断了。因为矩阵秩的计算要比行列式的计算快得多。
import numpy as npnp.linalg.matrix_rank(a)
有了矩阵秩的概念之后,我们后续的很多内容介绍起来都方便了许多,它也是矩阵领域当中非常重要的概念之一。
线性方程组的解
我们理解了矩阵的秩的概念之后,我们现学现用,看看它在线性方程组上的应用。
我们之前在介绍行列式的时候,曾经介绍过n元n个等式的方程组的解,可以用行列式表示。但是现实当中我们遇见的方程组并不一定是n元n等式的,我们推广到一般的情况来看。假设当下有一个n元m个等式的方程组:
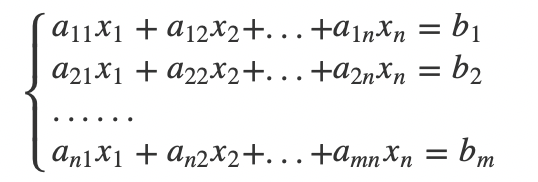
我们可以将它写成矩阵相乘的形式:
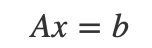

我们利用系数矩阵A和增广矩阵B=(A,b)的秩,可以和方便地看出线性方程组是否有解。我们先来看结论:
当R(A) < R(B)时无解
当R(A) = R(B) = n时,有唯一解
当R(A) = R(B) < n时,有无数解
证明的过程也很简单,主要就是利用矩阵秩和最简矩阵的定义。
我们假设R(A)=r,并将B矩阵化简成最简形式,假设得到的结果是:
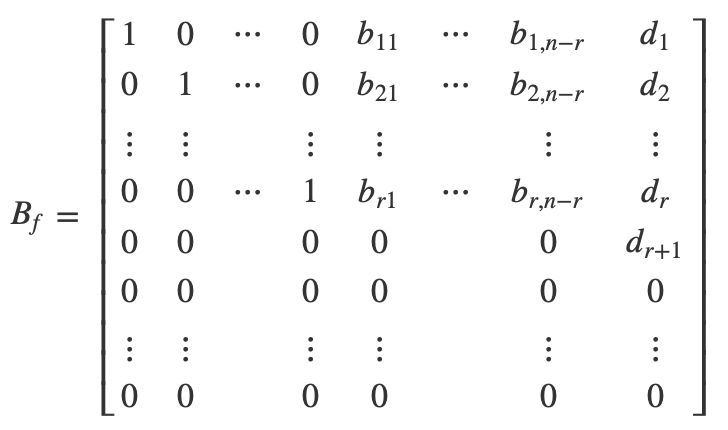
(1)显然,当R(A) < R(B)时,那么矩阵中的,那么第r + 1行对应的方程0 = 1矛盾,所以方程无解。
(2)如果R(A) = R(B) = r = n,那么矩阵中的,并且都不出现,所以我们可以直接写出方程组的解:
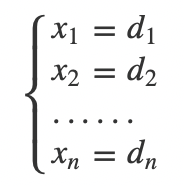
此时,方程组有唯一解
(3)如果R(A) = R(B) = r < n,则B中的
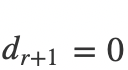 ,我们写出对应的解:
,我们写出对应的解:
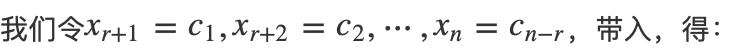
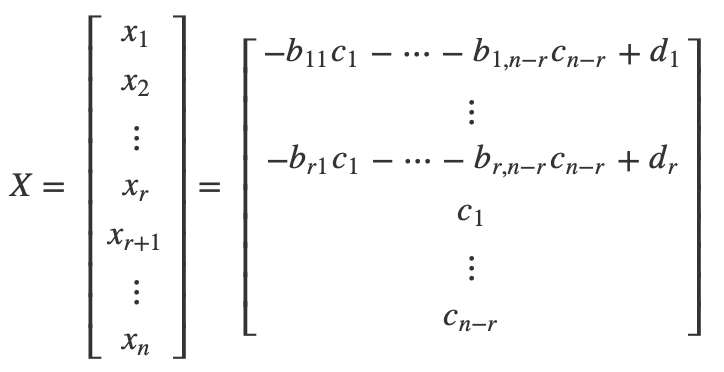
由于参数
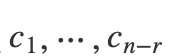 可以取任意值,所以方程有无数解。上面写出的解的形式即是线性方程组的通解。
可以取任意值,所以方程有无数解。上面写出的解的形式即是线性方程组的通解。
齐次线性方程组
如果我们将上面的线性方程组的常数项都置为0,就称为齐次线性方程组,如下:
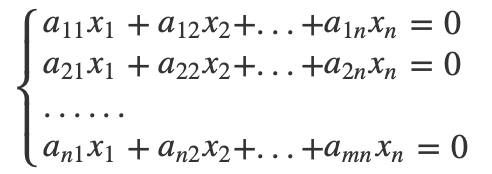
齐次方程组最大的特点就是当
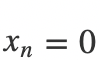 时一定有解,称为方程组的零解。我们还通过增广矩阵来判断,写出来其实还是刚才一样的形式:
时一定有解,称为方程组的零解。我们还通过增广矩阵来判断,写出来其实还是刚才一样的形式:

和非齐次线性方程组不同的是,我们可以断定
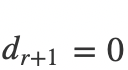 ,如此一来就不存在无解的情况。这个时候我们要判断的就是方程组是否存在非零解,我们一样通过矩阵的秩来判断,判断的条件也很简单,如果R(A) = n,则不存在非零解,如果R(A) < n,则存在无数组非零解。我们先写出R(A) = n的情况,这时候的矩阵Bf为:
,如此一来就不存在无解的情况。这个时候我们要判断的就是方程组是否存在非零解,我们一样通过矩阵的秩来判断,判断的条件也很简单,如果R(A) = n,则不存在非零解,如果R(A) < n,则存在无数组非零解。我们先写出R(A) = n的情况,这时候的矩阵Bf为:
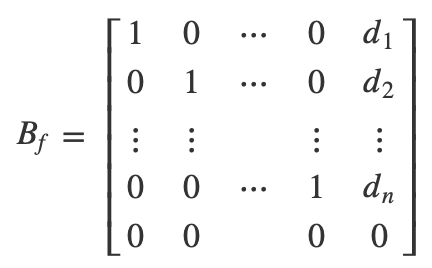
也就是说:
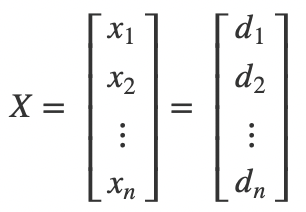

当R(A) < n时方程组和非齐次方程组类似,唯一不同的是可以确定
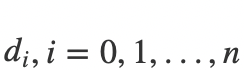 ,我们直接带入之前的通项公式,可以得到:
,我们直接带入之前的通项公式,可以得到:
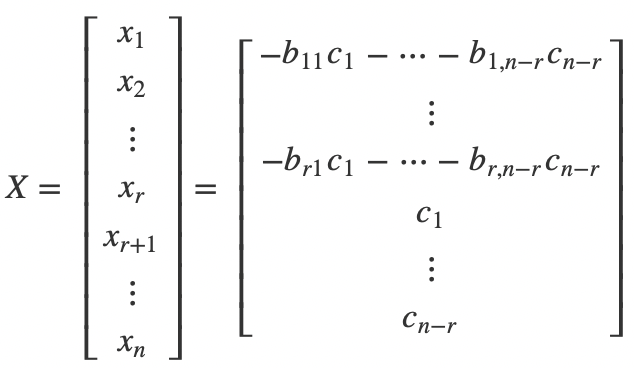
线性方程组的解的公式和计算本身其实并不重要。因为在实际的算法领域,用到的也不多。但是理解线性方程组对于理解后面的向量以及线性空间非常有帮助,文中的公式看着恐怖,但冷静下来真的去试着理解一下,会发现也就那么回事。