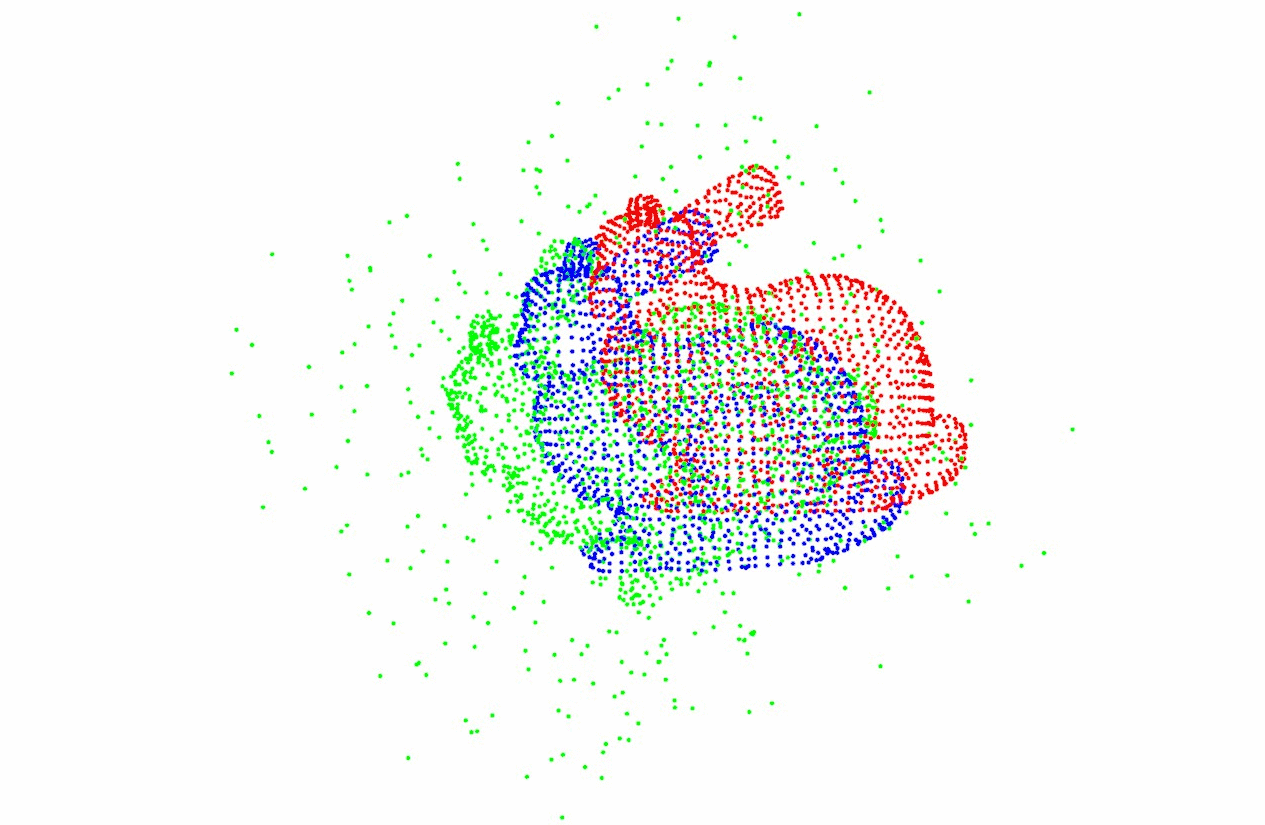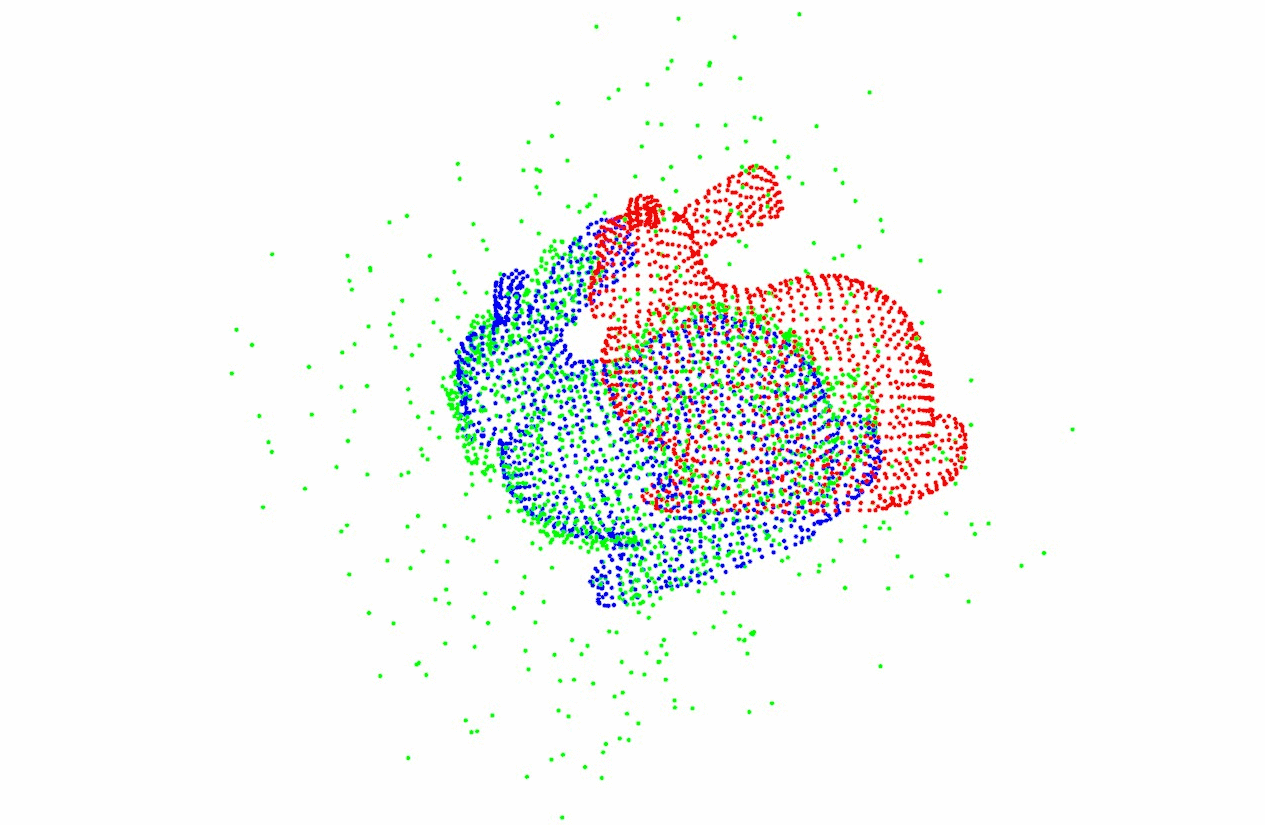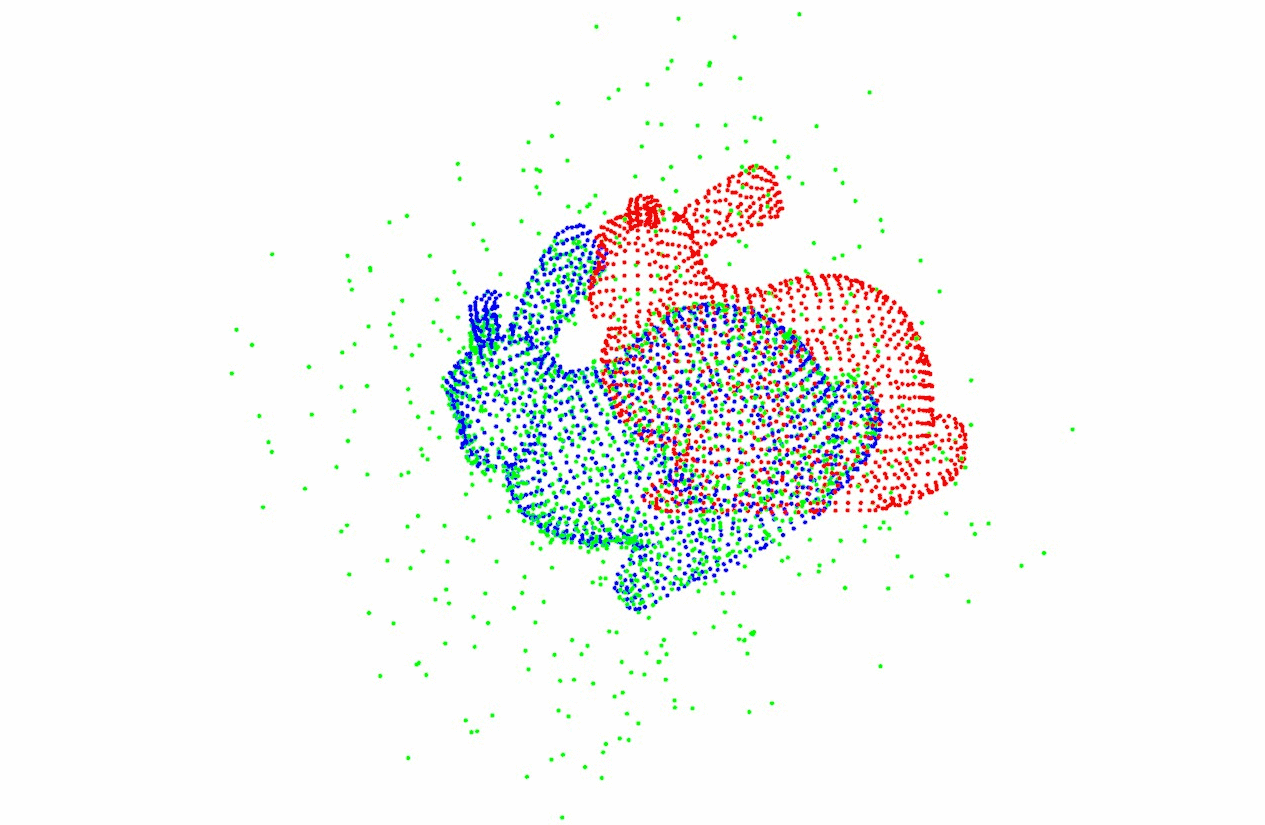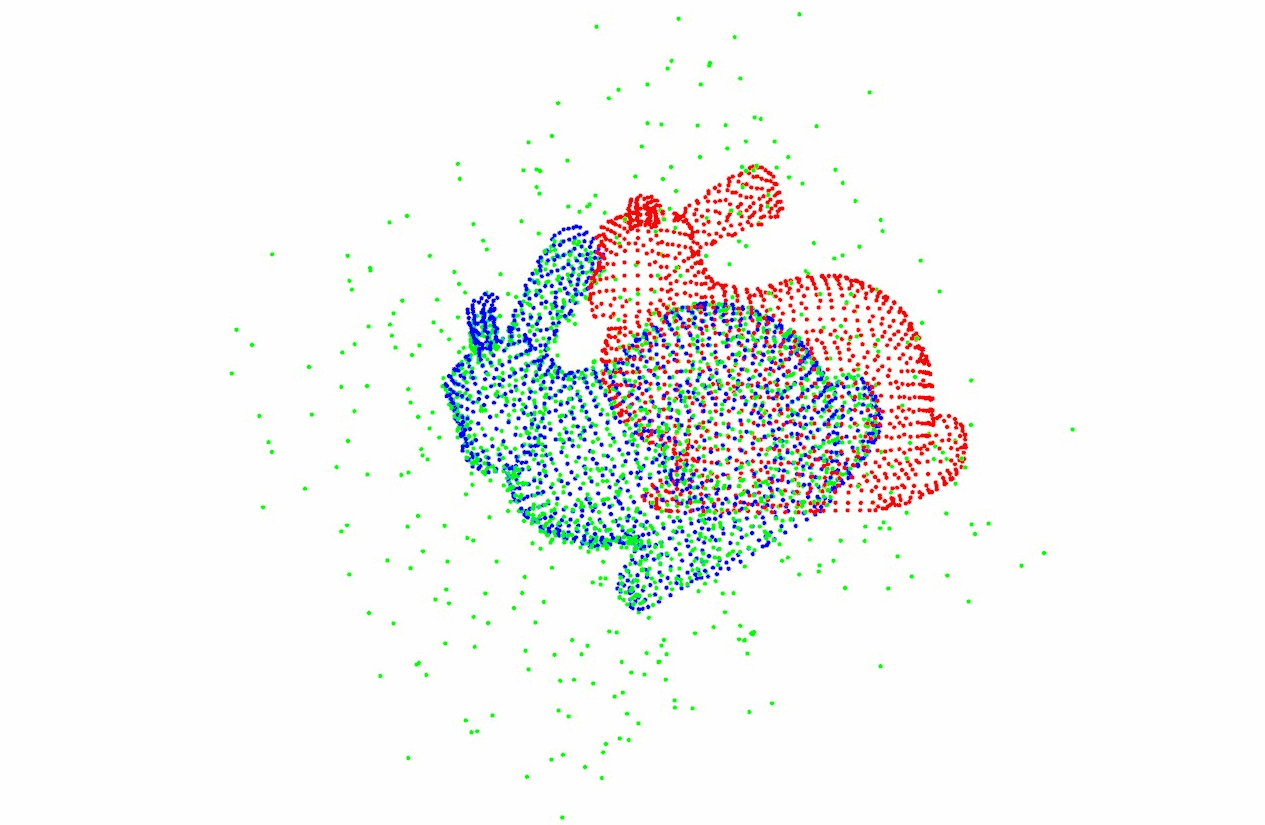
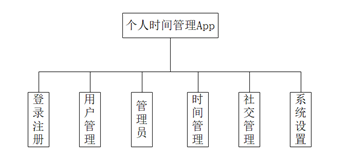
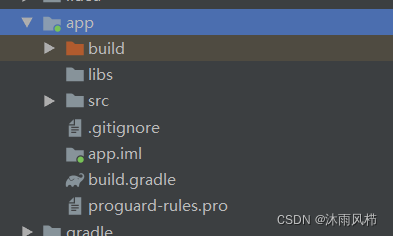
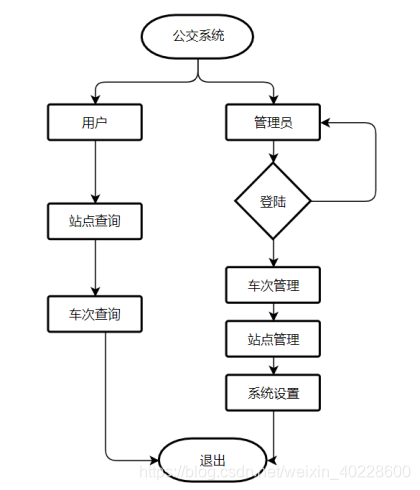
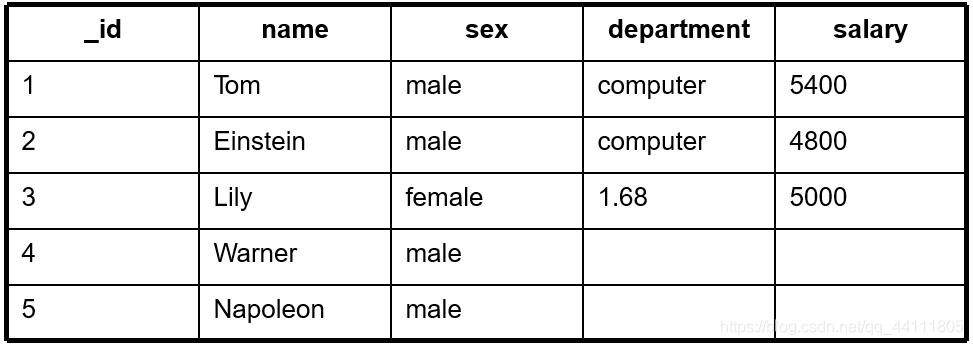
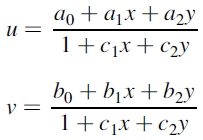图像配准在目标检测、模型重建、运动估计、特征匹配，肿瘤检测、病变定位、血管造影、地质勘探、航空侦察等领域都有广泛的应用。

每一种配准方法通常都针对某个具体问题而设计的，众多方法中，唯一的共性就是每个配准问题最终都要在变换空间中寻找一种最有的变换，这种变换能够使两幅图像之间在某种意义上达到匹配，但对于不同的应用领域，对图像类型的要求不同，就需要具体问题具体分析。

有研究者根据待配准图像之间的关系，将图像配准分为多源图像配准、基于模板的配准、多角度图像配准、时间序列图像配准四大类。详见下图

 

目前，较为常用的是按照在图像配准算法中对待配准图像信息的处理方法进行分类，可以分为三类：

（1）基于待配准图像灰度信息的配准方法

以整幅图像的灰度信息为依据，建立待配准图像和基准参考图像之间的相似性度量，利用某种搜索算法，寻找出使得相似度量达到最优值的变换模型参数。也称之为直接配准法；

 

（2）基于待配准图像变换域内信息的配准方法

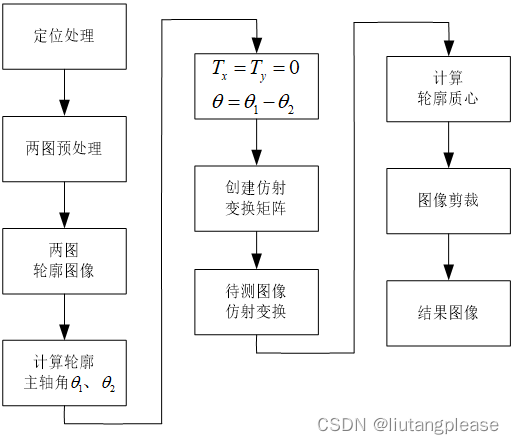
通常是利用傅里叶变换为基础，进行频域内的配准。傅里叶变换能够用于具有平移、旋转、缩放的图像配准中是因为

 （a