什么是产品关联度分析

关联分析是发现交易数据库中不同商品（项）之间的联系，主要应用于电商网站 推荐、线下零售门店商品摆放等场景中。
关联规则：

• 支持度（support）：数据集中包含某几个特定项的概率。比如在1000次的 商品交易中同时出现了A和B的次数是50次，那么此关联的支持度为5%。
• 置信度（Confidence）：在数据集中已经出现A时，B发生的概率，置信度 的计算公式是 ：A与B同时出现的概率/A出现的概率。
• 提升度就是在购买A产品这个条件下购买B产品的可能性与没有这个条件下购买B 产品的可能性之比（置信度/无条件概率）。 一般而言，提升度如果小于1，则该推荐规则不应该被使用。

举个例子，有如下购物车，ABCDE分别代表不同商品

规则	支持度	置信度	提升度
A–D	0.4	0.67	1.12
C–A	0.4	0.5	0.83
A–C	0.4	0.67	0.83
B&C–D	0.2	0.33	0.55

如何计算的呢？
支持度：商品A和D中，他们在购物篮上同时出现的次数2次，占总购物篮的百分之40%
置信度：A出现的概率是0.6，按照公式A与D同时出现的概率/A出现的概率，0.4÷0.6=0.67
提升度：置信度/无条件概率，0.67÷（D的无条件概率：3÷5=0.6） = 1.12

什么是购物篮分析

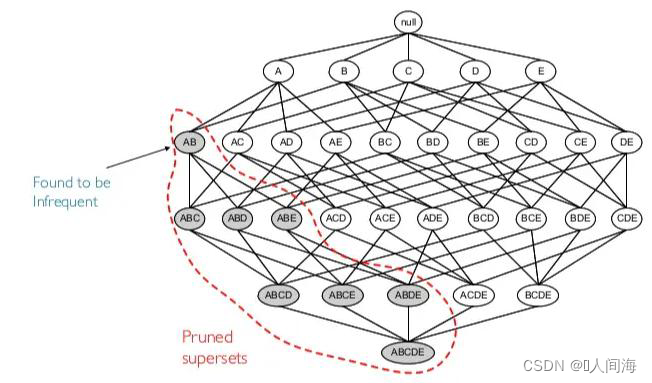
业界一般将单个客户一次购买商品的总和称为一个购物篮，购物篮分析就是针对商品的相关性分析。 因为最初这种关联分析主要是在超市应用广泛，所以也称为“购物篮分析”。购物篮分析有个Apriori算法（先验算法）
购物篮分析要点：

• 找到正确的物品组合
• 找到用户对应不同组合的购买时间
• 找到用户对应不同组合的购买顺序

举个例子
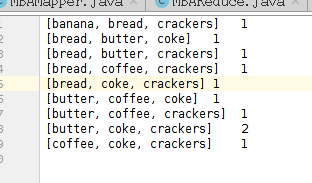
有如下多个交易单

步骤一：计算不同商品的交易频次

步骤二：根据最低支持度筛选商品（假定最低支持度为百分之50）

计算不同组合的交易频次
组合计算公式：

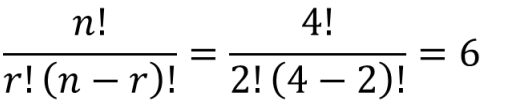
n表示商品数量，r表示一个组合的商品数量

步骤四： 根据最低支持度筛选组合 （最低支持度为50%）

步骤五： 计算不同组合的交易频次 （三种商品）

步骤六： 根据最低支持度筛选组合 （最低支持度为50%）

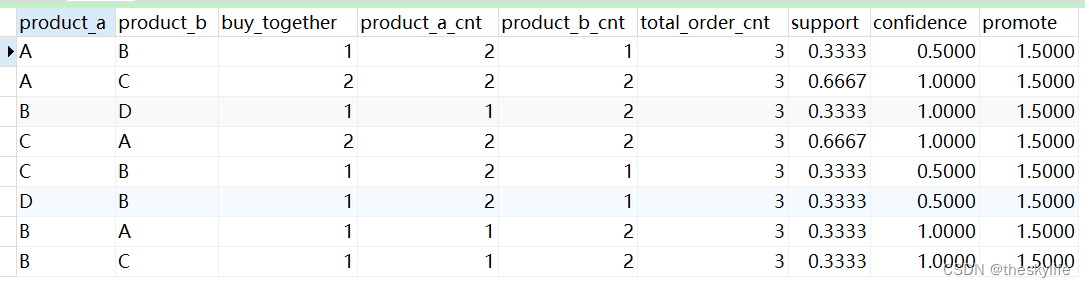
购物篮分析的应用

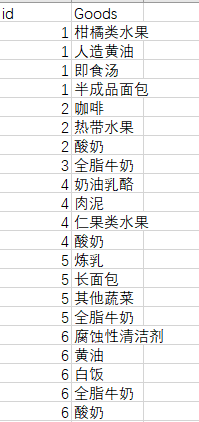
假设有如下订单：购物篮id与售出商品

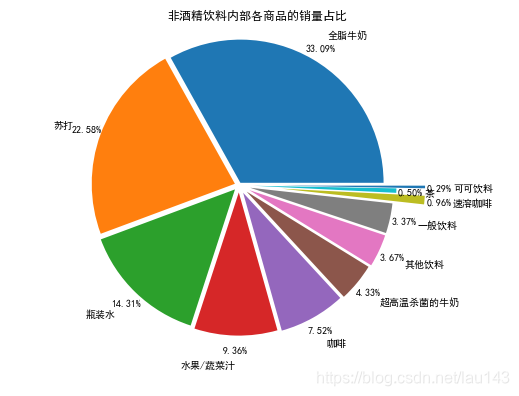
热销产品的情况如下

我们对数据使用Apriori算法，首先得将数据预处理一下，将同一订单（id）下的商品整合到一起

import pandas as pd
inputfile='/content/GoodsOrder.csv'
data = pd.read_csv(inputfile,encoding = 'gbk')# 根据id对“Goods”列合并，并使用“，”将各商品隔开
data['Goods'] = data['Goods'].apply(lambda x:','+x)
data = data.groupby('id').sum().reset_index()# 对合并的商品列转换数据格式
data['Goods'] = data['Goods'].apply(lambda x :[x[1:]])
data_list = list(data['Goods'])# 分割商品名为每个元素
data_translation = []
for i in data_list:p = i[0].split(',')data_translation.append(p)

得到如下格式就可以了

from numpy import *def loadDataSet():return [['a', 'c', 'e'], ['b', 'd'], ['b', 'c'], ['a', 'b', 'c', 'd'], ['a', 'b'], ['b', 'c'], ['a', 'b'],['a', 'b', 'c', 'e'], ['a', 'b', 'c'], ['a', 'c', 'e']]def createC1(dataSet):C1 = []for transaction in dataSet:for item in transaction:if not [item] in C1:C1.append([item])C1.sort()# 映射为frozenset唯一性的，可使用其构造字典return list(map(frozenset, C1))     # 从候选K项集到频繁K项集（支持度计算）
def scanD(D, Ck, minSupport):ssCnt = {}for tid in D:   # 遍历数据集for can in Ck:  # 遍历候选项if can.issubset(tid):  # 判断候选项中是否含数据集的各项if not can in ssCnt:ssCnt[can] = 1  # 不含设为1else:ssCnt[can] += 1  # 有则计数加1numItems = float(len(D))  # 数据集大小retList = []  # L1初始化supportData = {}  # 记录候选项中各个数据的支持度for key in ssCnt:support = ssCnt[key] / numItems  # 计算支持度if support >= minSupport:retList.insert(0, key)  # 满足条件加入L1中supportData[key] = support  return retList, supportDatadef calSupport(D, Ck, min_support):dict_sup = {}for i in D:for j in Ck:if j.issubset(i):if not j in dict_sup:dict_sup[j] = 1else:dict_sup[j] += 1sumCount = float(len(D))supportData = {}relist = []for i in dict_sup:temp_sup = dict_sup[i] / sumCountif temp_sup >= min_support:relist.append(i)
# 此处可设置返回全部的支持度数据（或者频繁项集的支持度数据）supportData[i] = temp_supreturn relist, supportData# 改进剪枝算法
def aprioriGen(Lk, k):retList = []lenLk = len(Lk)for i in range(lenLk):for j in range(i + 1, lenLk):  # 两两组合遍历L1 = list(Lk[i])[:k - 2]L2 = list(Lk[j])[:k - 2]L1.sort()L2.sort()if L1 == L2:  # 前k-1项相等，则可相乘，这样可防止重复项出现# 进行剪枝（a1为k项集中的一个元素，b为它的所有k-1项子集）a = Lk[i] | Lk[j]  # a为frozenset()集合a1 = list(a)b = []# 遍历取出每一个元素，转换为set，依次从a1中剔除该元素，并加入到b中for q in range(len(a1)):t = [a1[q]]tt = frozenset(set(a1) - set(t))b.append(tt)t = 0for w in b:# 当b（即所有k-1项子集）都是Lk（频繁的）的子集，则保留，否则删除。if w in Lk:t += 1if t == len(b):retList.append(b[0] | b[1])return retListdef apriori(dataSet, minSupport=0.2):
# 前3条语句是对计算查找单个元素中的频繁项集C1 = createC1(dataSet)D = list(map(set, dataSet))  # 使用list()转换为列表L1, supportData = calSupport(D, C1, minSupport)L = [L1]  # 加列表框，使得1项集为一个单独元素k = 2while (len(L[k - 2]) > 0):  # 是否还有候选集Ck = aprioriGen(L[k - 2], k)Lk, supK = scanD(D, Ck, minSupport)  # scan DB to get LksupportData.update(supK)  # 把supk的键值对添加到supportData里L.append(Lk)  # L最后一个值为空集k += 1del L[-1]  # 删除最后一个空集return L, supportData  # L为频繁项集，为一个列表，1，2，3项集分别为一个元素# 生成集合的所有子集
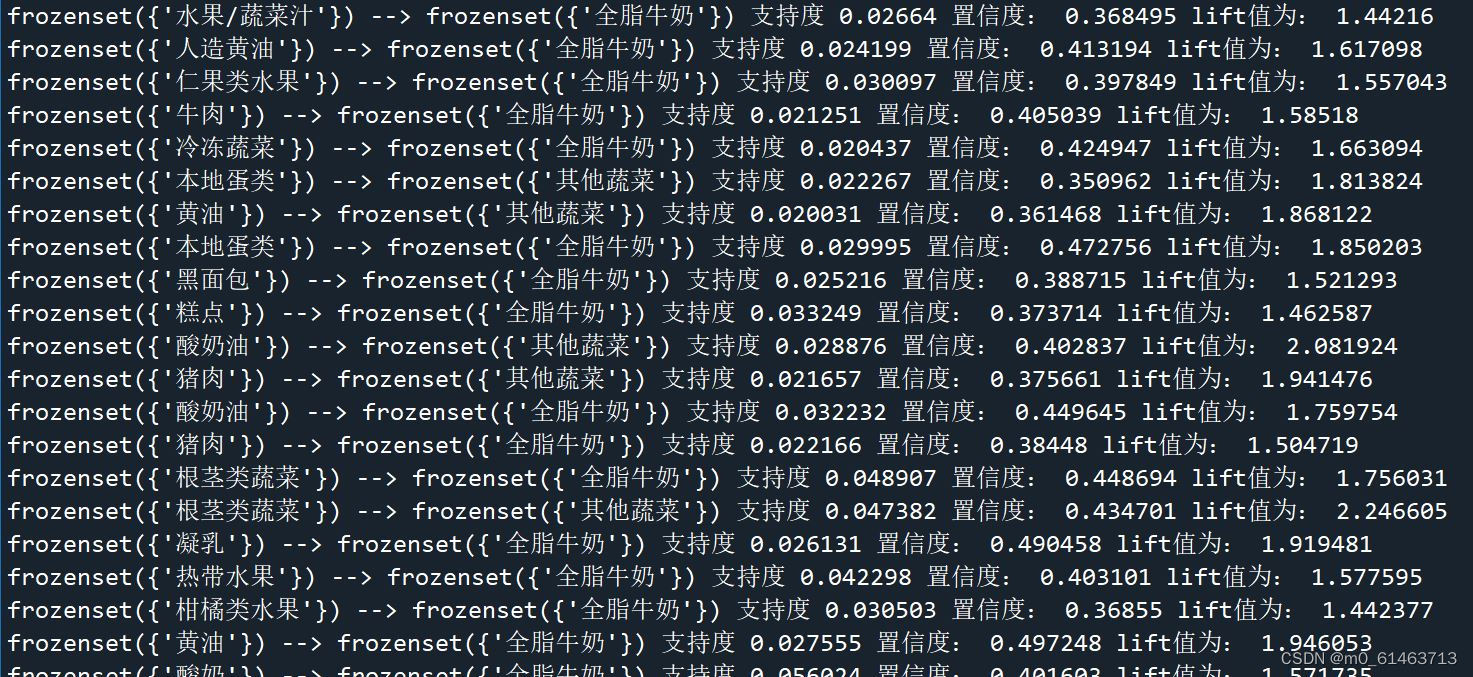
def getSubset(fromList, toList):for i in range(len(fromList)):t = [fromList[i]]tt = frozenset(set(fromList) - set(t))if not tt in toList:toList.append(tt)tt = list(tt)if len(tt) > 1:getSubset(tt, toList)def calcConf(freqSet, H, supportData, ruleList, minConf=0.7):for conseq in H:  #遍历H中的所有项集并计算它们的可信度值conf = supportData[freqSet] / supportData[freqSet - conseq]  # 可信度计算，结合支持度数据# 提升度lift计算lift = p(a & b) / p(a)*p(b)lift = supportData[freqSet] / (supportData[conseq] * supportData[freqSet - conseq])if conf >= minConf and lift > 1:print(freqSet - conseq, '-->', conseq, '支持度', round(supportData[freqSet], 6), '置信度：', round(conf, 6),'lift值为：', round(lift, 6))ruleList.append((freqSet - conseq, conseq, conf))# 生成规则
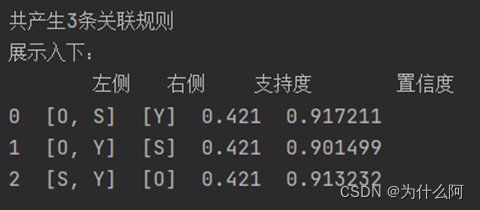
def gen_rule(L, supportData, minConf = 0.7):bigRuleList = []for i in range(1, len(L)):  # 从二项集开始计算for freqSet in L[i]:  # freqSet为所有的k项集# 求该三项集的所有非空子集，1项集，2项集，直到k-1项集，用H1表示，为list类型,里面为frozenset类型，H1 = list(freqSet)all_subset = []getSubset(H1, all_subset)  # 生成所有的子集calcConf(freqSet, all_subset, supportData, bigRuleList, minConf)return bigRuleListif __name__ == '__main__':dataSet = data_translationL, supportData = apriori(dataSet, minSupport = 0.02)rule = gen_rule(L, supportData, minConf = 0.35)

产品定位分析