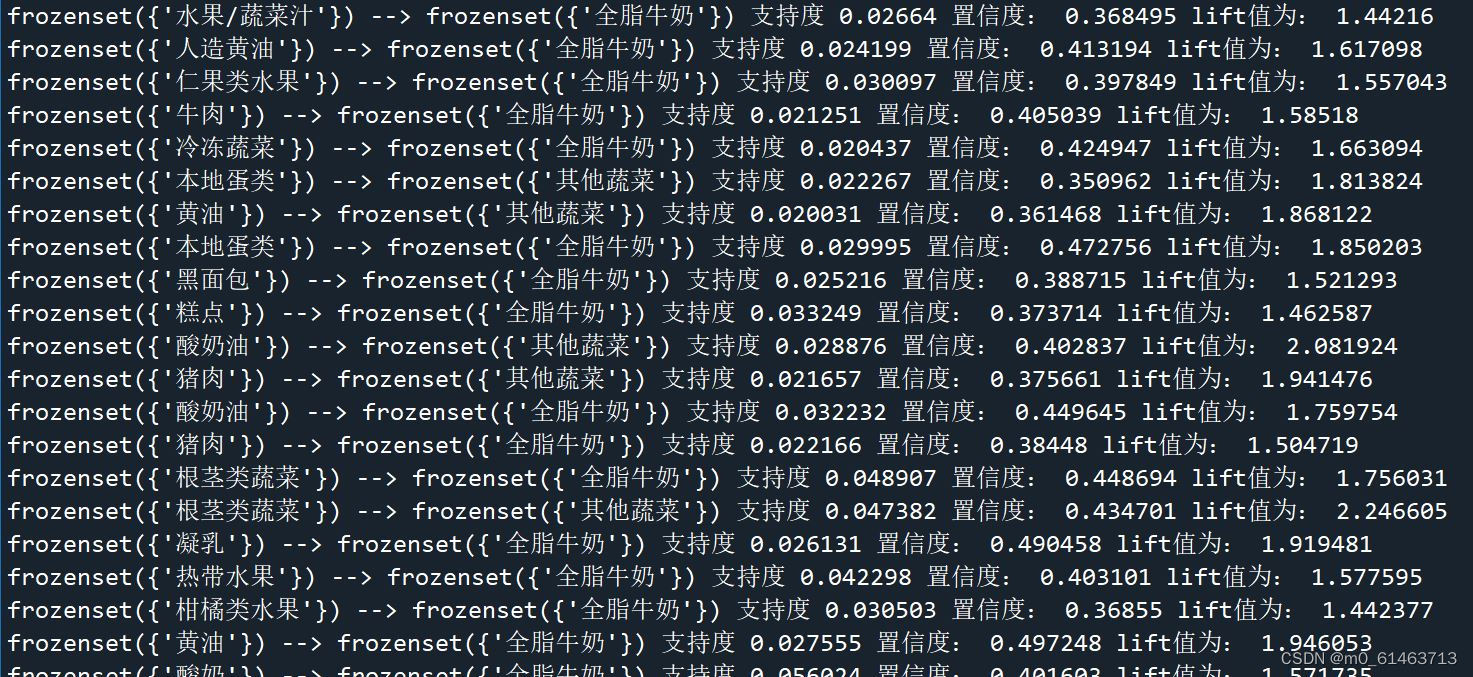
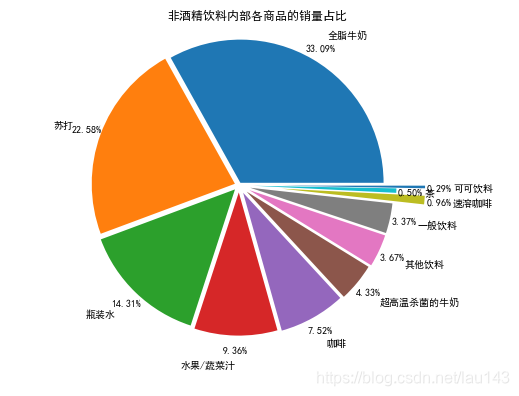
从购物篮分析到关联规则挖掘 Apriori算法

​ 随着大量数据不断的收集和存储，许多业界人士对于从他们的数据库中挖掘知识越来越感兴趣。对于商场而言，从大量的商务事务记录中发现有价值的的关联关系，可以为货物摆放和分析顾客购物习惯等许多商务决策过程提供帮助。

购物篮分析

​ 购物篮分析是一个典型的关联规则挖掘实例，例如如下图所示的9次购物中不同顾客购物篮中的商品，以此可以分析商品之间的关联和顾客的购物习惯，可以分析顾客可能会在一次购物中同时购买哪些商品。

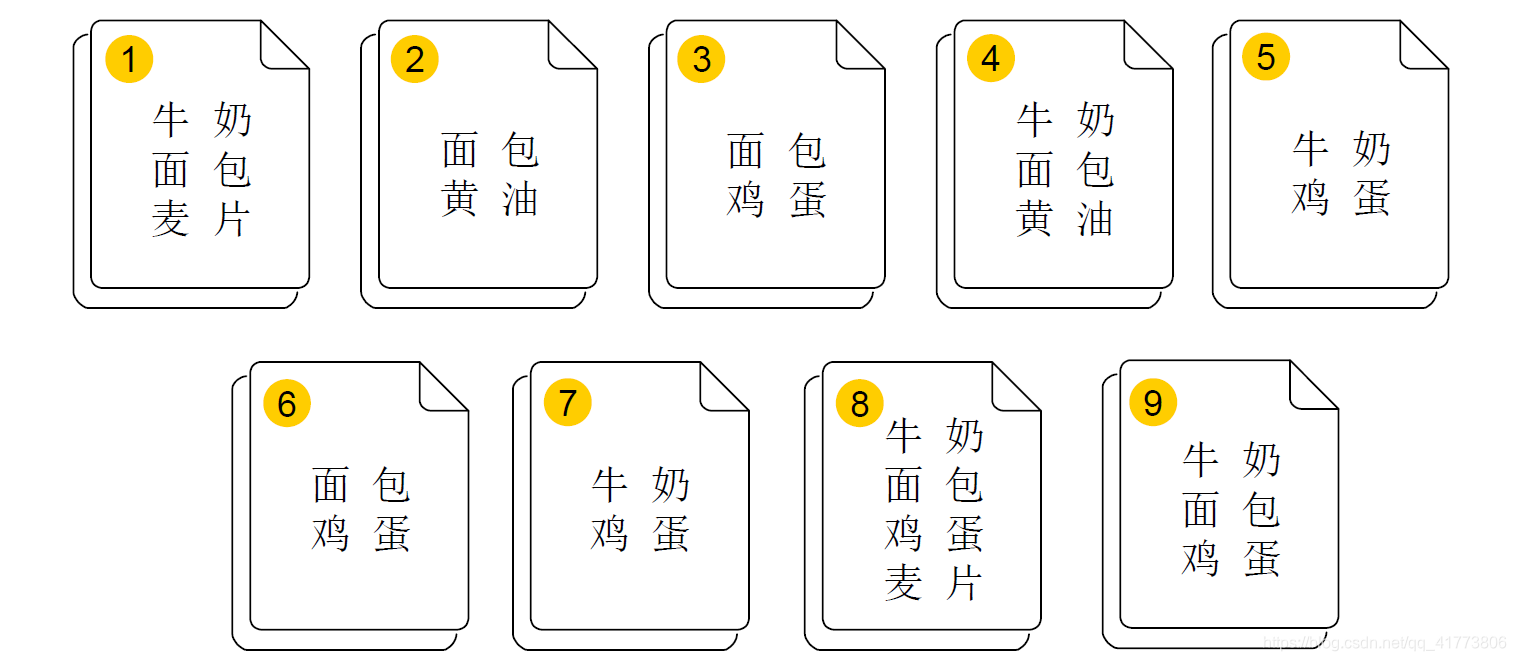
​ 一种简单的分析策略是通过搜索上述9个购买事务中的商品集合，那些经常出现在同一个商品集合中的商品可以认为他们之间存在关联关系，有很大概率会被顾客同时购买。

频繁项集

​ 为了便于分析，我们为商品引入数字ID，购买事务也用事务编号代替，上述9个购买事务用数字化表示如下表所示：

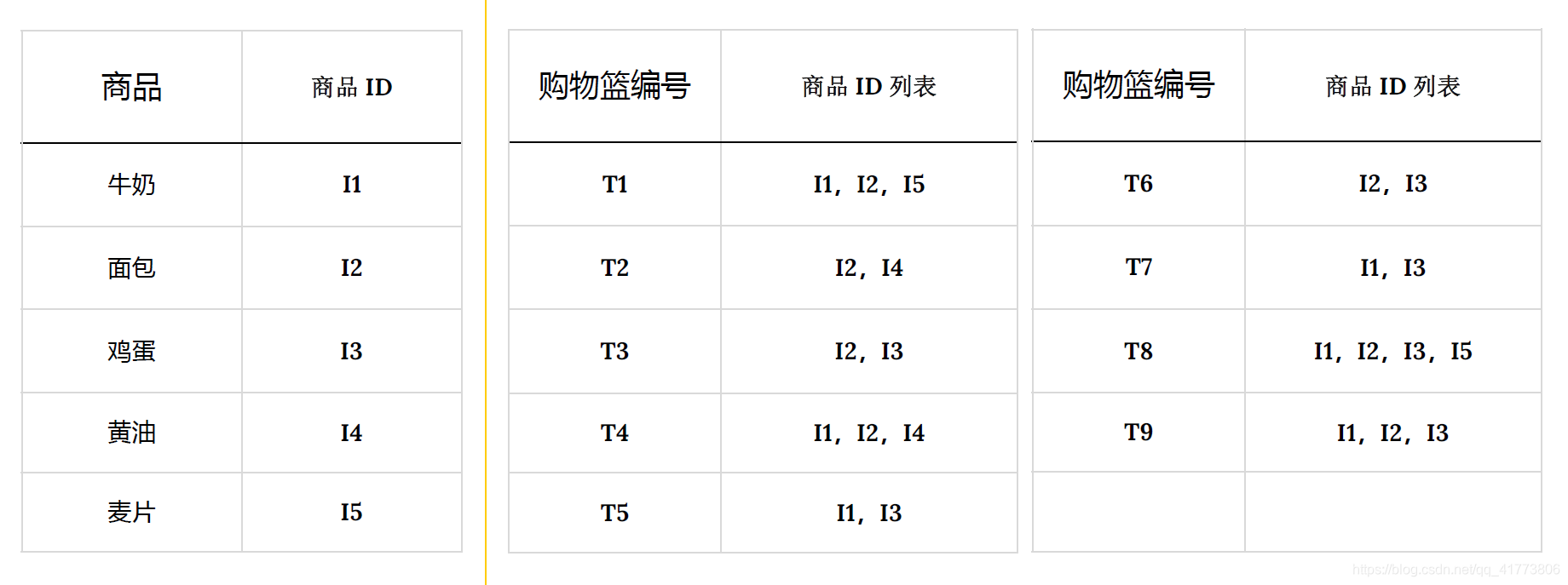
​ 同时，我们引入一些基础概念：

• 项集 itemset：在购物篮分析中一个购买事务就是一个项集，购物篮中的商品就是该项集的项 ， 包含 k 个项的项集称为 k 项集
• 频度/支持度计数 support_count：包含指定项集的事务数称为支持度计数，在购物篮分析中指的是同一个商品集合出现的次数
• 频繁项集 frequent itemset：满足最小支持度阈值的项集称为频繁项集，在购物篮分析中即为多次出现且满足最小频度的商品集合。

​ 我们预设频繁项集的最小频度为2，可以直观的看出 $I1,I2,I3$ 和 $I1,I2,I5$ 被同时购买的次数是2，所以这两种商品组合可以被视为频繁项集，且这些商品之间可能存在关联关系。

关联规则

​ 频繁项集中的项可能存在关联关系，如何得出这种关系呢？一种简单的关联关系分析方法就是计算商品组合之间的条件概率，以 $I1,I2,I5$ 为例得出商品之间关系过程如下：

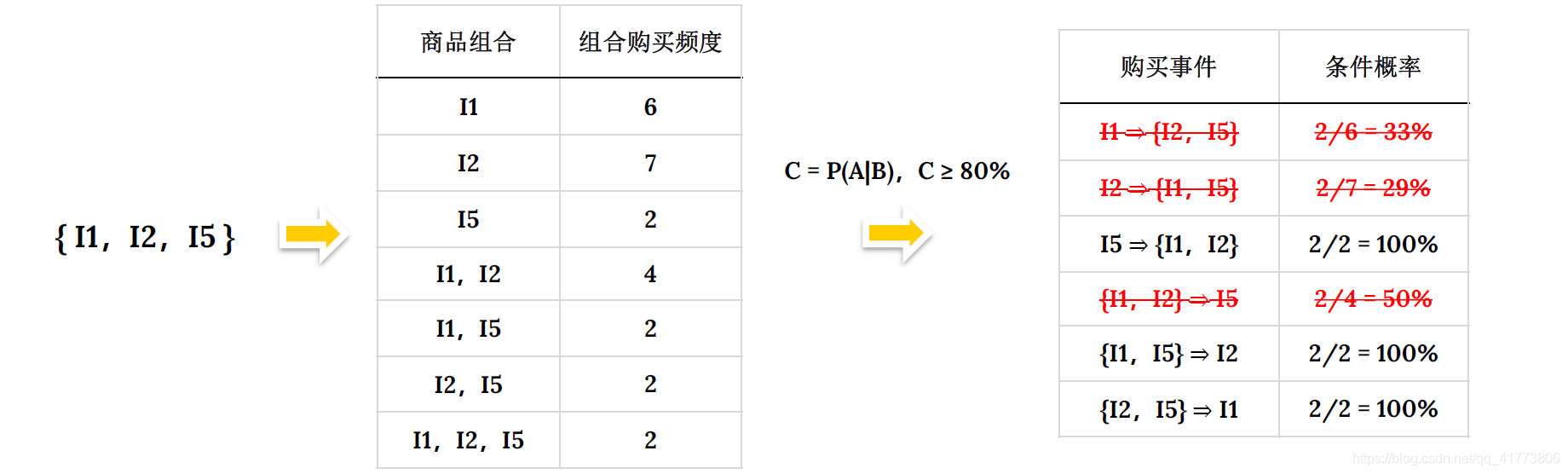
​ 我们考虑最小条件概率为 80% 的购买模式才被视为有效的关联关系，则只有第 3 条、第 5 条和第 6 条是有效的商品关联关系。对应到商品就是： 麦片 > (牛奶，面包)；(牛奶，麦片) > 面包； (面包，麦片) > 牛奶。

​ 上面得到的这种商品的购买模式可以用关联规则的形式表示，例如：(牛奶，麦片) > 面包： { I 1 , I 5 } = > I 2 \left\{I1, I5\right\} => I2 {I1,I5}=>I2 可以使用如下的关联规则表示：
{ I 1 , I 5 } = > I 2 [ s u p p o r t = 22 % ; c o n f i d e n c e = 100 % ] \left\{I1, I5\right\} => I2[support = 22\%; confidence = 100\%] {I1,I5}=>I2[support=22%;confidence=100%]
​ 其中，关联规则的支持度 support 和置信度 confidence 是规则兴趣度的两个度量：

• 支持度 support：支持度是指事件 A 和事件 B 同时发生的概率，即联合概率：

$$support(A=>B)=P(AB)=\frac{support\_count(A\bigcap B)}{support\_count(all)}$$

• 置信度 confidence：置信度指的是发生事件 A 的情况下发生事件 B 的概率，即条件概率：

$$confidence(A=>B)=P(B|A)=\frac{support\_count(A\bigcup B)}{support\_count(A)}$$

• 强规则：同时满足预定义的最小支持度 (min_𝑠𝑢𝑝𝑝𝑜𝑟𝑡)和最小置信度 (min_𝑐𝑜𝑛𝑓𝑖𝑑𝑒𝑛𝑐𝑒)的规则称为强规则。

关联规则挖掘步骤

1. 找出所有的频繁项集：这些项集的每一个频繁出现的次数大于等于预定义的最小支持度计数(min_𝑠𝑢𝑝𝑝𝑜𝑟𝑡_𝑐𝑜𝑢𝑛𝑡)
2. 由频繁项集产生强关联规则：这些规则必须同时满足预定义的最小支持度(min_𝑠𝑢𝑝𝑝𝑜𝑟𝑡)和最小置信度(min_𝑐𝑜𝑛𝑓𝑖𝑑𝑒𝑛𝑐𝑒)

Apriori 算法

​ 超市中的商品种类数以万计，假设我们要分析其中 100 种商品的关联关系那这一百种商品可以构成的项集数目如下：

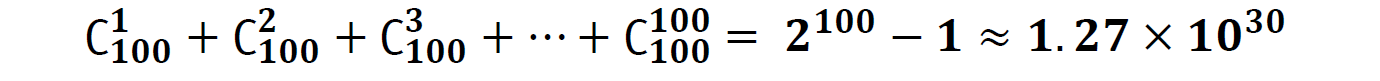
​ 可见随着项数目的增加，项集的数目是呈指数级增长的，这将带来极大的计算和存储问题。为了提高频繁项集的搜索效率，Apriori 算法使用一种称为先验性质的重要性质用于压缩搜索空间。

• 先验性质描述为：频繁项集的所有非空子集也一定是频繁的。
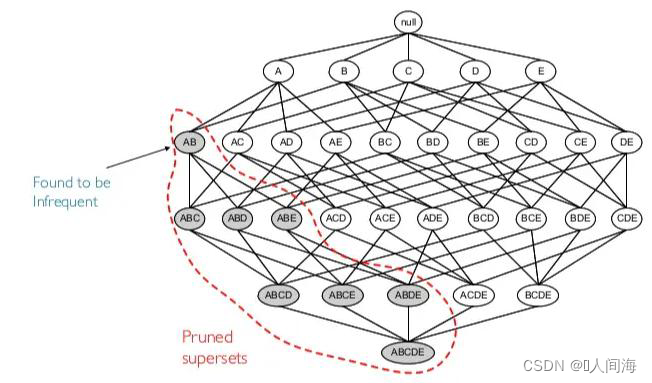
• 先验性质的逆否命题： 如果一个项集是非频繁的，那么它的所有超集也都是非频繁的。

​ 如下图所示，例如项集 { I 1 , I 2 } \left\{I1,I2\right\} {I1,I2}是非频繁的，那么它的超集 { I 1 , I 2 , I 3 } , { I 1 , I 2 , I 4 } , { I 1 , I 2 , I 3 , I 4 } \left\{I1,I2,I3\right\},\left\{I1,I2,I4\right\},\left\{I1,I2,I3,I4\right\} {I1,I2,I3},{I1,I2,I4},{I1,I2,I3,I4}都是非频繁项集，采用这种性质可以大幅度的压缩频繁项集的产生和计算。

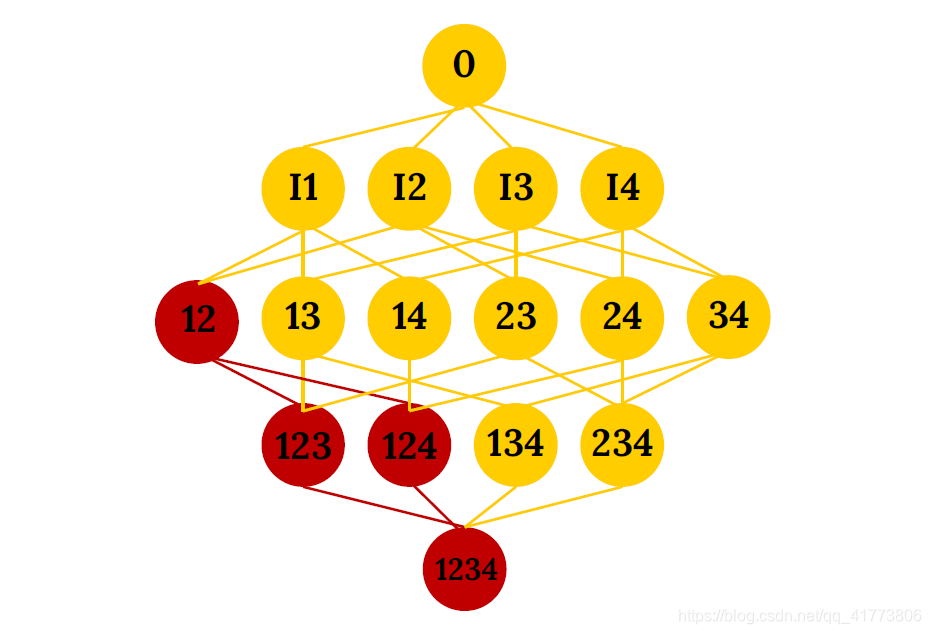
Apriori 算法原理

​ 如下图所示，Apriori 算法是一种逐层搜索的迭代方法，使用 k 项集去搜索 k+1 项。首先， 生成频繁 1 项集： 扫描数据库，累计每个项的计数，收集满足最小支持度的项形成频繁 1 项集记为 𝐿1。然后，基于 𝐿1找出频繁 2 项集记为 𝐿2 基于𝐿2找出频繁 3 项集记为 𝐿3，如此逐层迭代搜索，直到不能在产生新的频繁 k 项集。

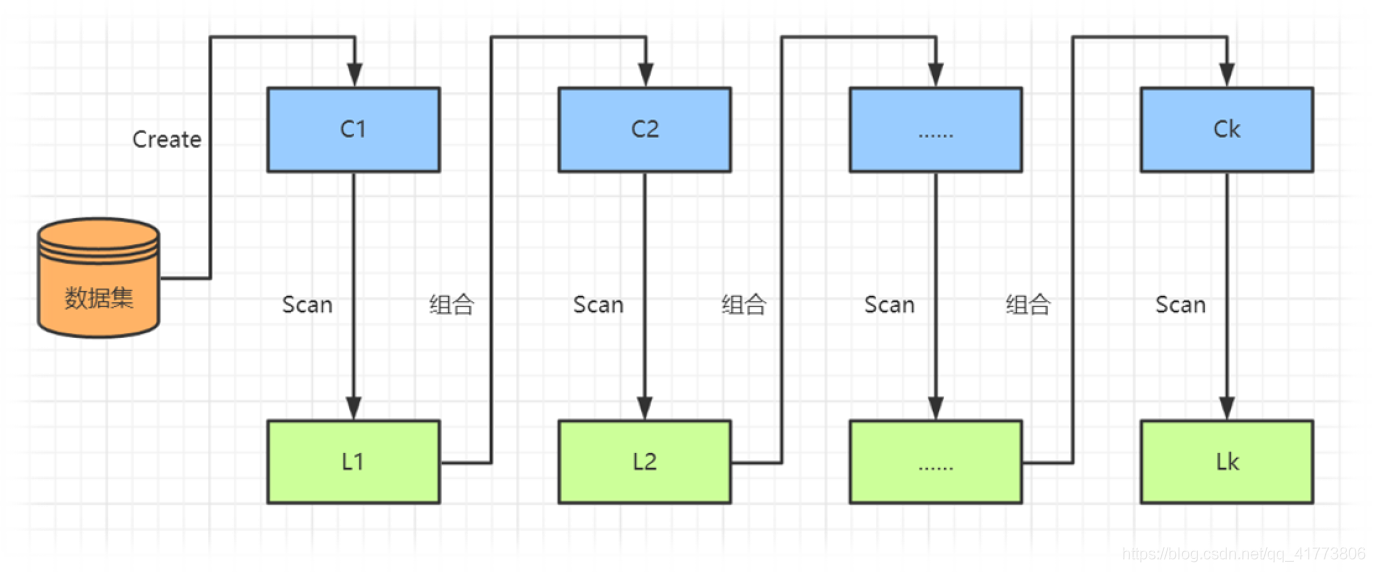
​ Apriori 算法中除了第一层频繁项集挖掘，后面的逐层迭代都由以下两个步骤组成：

连接步生成候选项集集合

​ Apriori 算法在每一层搜索迭代中，通过将上一层频繁项集的集合 𝐿_𝑘−1与自身连接产生候选 k 项集的集合 𝐶𝑘。

​ 𝐿_𝑘−1中频繁项集 𝑙1 和 𝑙2 可连接的条件是： 𝑙1 和 𝑙2 的 k-2 个项是相同的。

剪枝步生成频繁项集集合

​ 连接步生成的候选 k 项集的集合 𝐶𝑘 是待求的频繁 k 项集集合 L𝑘的超集。从 𝐶𝑘 中找出频繁项集需要反复扫描数据库，确定 𝐶𝑘 中每个候选的计数，并根据最小支持度确定 L𝑘。
​ 当事务中项的数目很大时，将产生巨大的搜索空间，为了压缩 𝐶𝑘，使用先验性质对 𝐶𝑘 进行剪枝。即任何非频繁的 k-1 项集都不是频繁 k 项集的子集。所以，如果一个候选 k 项集的 k-1 项子集不在 L_𝑘-1 中，则该候选是非频繁的并从 𝐶𝑘 中剔除。

Apriori 算法实例

​ 基于前面购物篮分析例子中的 9 个事务，使用 Apriori 算法挖掘频繁项集。预设最小支持度为 20% 即最小支持度计数大于等于 2 ，最小置信度为 80%。

1. 挖掘频繁 1 项集：扫描数据库 D 中的所有事务，对每一个项的出现次数计数，得到候选 1 项集集合 𝐶1，根据最小支持度 20% 即最小支持度计数为 2 确定频繁 1 项集集合 𝐿1。

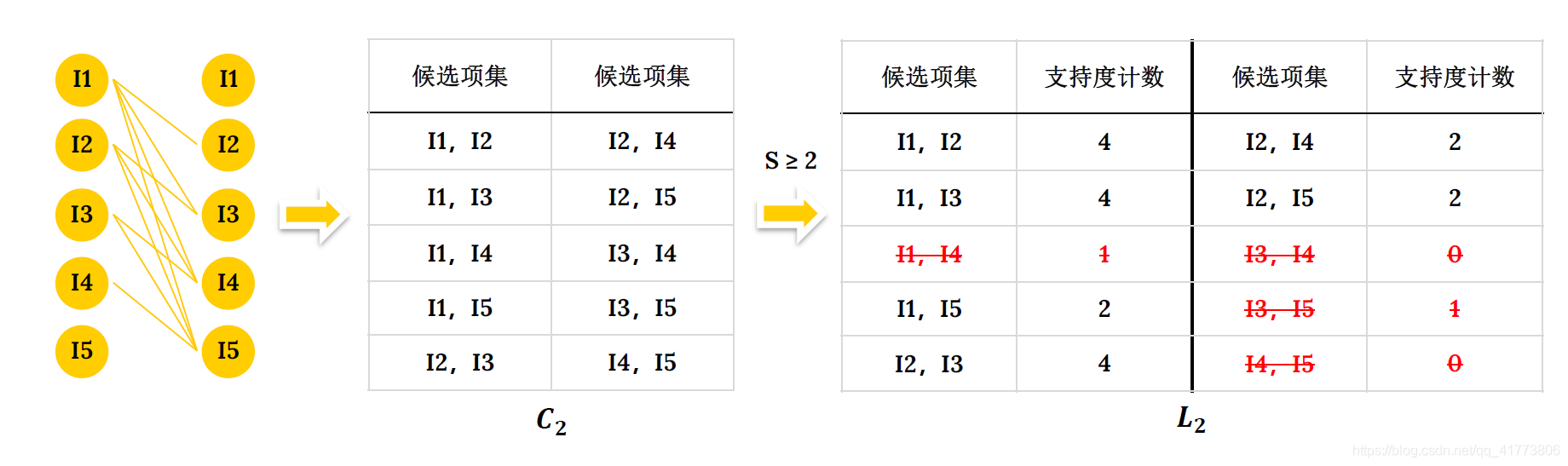
2. 挖掘频繁2项集：首先，连接步： 将频繁 1 项集集合中的元素进行连接产生候选 2 项集集合 𝐶2。然后，剪枝步： 𝐶2 中所有候选的子集都是频繁的，所以不删除任何候选。最后，确定频繁项集 ：扫描数据库 D 中的所有事务，对 𝐶2中的每一个候选项集的出现次数计数 ，根据最小支持度确定频繁 2 项集 𝐿2。

3. 挖掘频繁3项集：首先，连接步： 将频繁 2 项集集合中的元素进行连接产生候选 3 项集集合 𝐶3。然后，剪枝步： 检查 𝐶3 中候选项集的子集是否都是频繁的，如果存在非频繁的子集，将该候选项集从 𝐶3 中删除。最后，确定频繁项集 ：扫描数据库 D 中的所有事务，对 𝐶3 中的每一个候选项集的出现次数计数 ，根据最小支持度确定频繁 3 项集 𝐿3。

4. 停止寻找频繁项集： { I 1 , I 2 , I 3 } \left\{I1,I2,I3\right\} {I1,I2,I3} 和 { I 1 , I 2 , I 5 } \left\{I1,I2,I5\right\} {I1,I2,I5} 连接的唯一个候选项集是 { I 1 , I 2 , I 3 , I 5 } \left\{I1,I2,I3,I5\right\} {I1,I2,I3,I5}，但是其子集 { I 1 , I 3 , I 5 } \left\{I1,I3,I5\right\} {I1,I3,I5}和 { I 2 , I 3 , I 5 } \left\{I2,I3,I5\right\} {I2,I3,I5} 都是非频繁的，该候选项集将被剪去得到的候选 4 项集集合 𝐶4 为空，算法终止。所以最终得到的最大频繁项集是 { I 1 , I 2 , I 3 } \left\{I1,I2,I3\right\} {I1,I2,I3} 和 { I 1 , I 2 , I 5 } \left\{I1,I2,I5\right\} {I1,I2,I5} 。

5. 由频繁项集产生关联规则：关联规则产生，首先，对于每个频繁项集 𝑙，产生 𝑙的所有非空子集集合 𝑆；然后，对于 𝑙的每个非空子集 𝑠, 𝑙 在 𝑠下的条件概率满足最小置信度 (min_𝑐𝑜𝑛𝑓𝑖𝑑𝑒𝑛𝑐𝑒) 则可以输出规则 𝑠⇒(𝑙−𝑠)，这个规则是满足最小支持度和置信度的强规则。
   

Apriori 算法Python实现

# 产生频繁1项集
def scanD(D, Ck,minSupport) :#识别频繁项目集S = {}for i in D:for j in Ck:if j.issubset(i): if j not in S.keys():S[j] = 1else:S[j] += 1numItems = float(len(D)) L= []N=[]supportData = {} #候选集项Ck的支持度字典(key:候选项，value: 文持度)for key in S:support = S[key] / numItemssupportData[key] = supportif support >= minSupport:L. append(key)else:N.append(key)return L,N,supportData# Apriori算法 连接步和剪枝步
def aprioriGen(Lk,k,N):Ck=[]lenLk = len(Lk)for i in range(lenLk):# 连接步 (子连接运算)for j in range(i + 1,lenLk):L1 = list(Lk[i])[:k - 2]L1.sort()L2 = list(Lk[j])[:k - 2]L2.sort()if L1==L2:Ck.append(Lk[i]|Lk[j])#加入并集# 剪枝步 把子集中有属于非频繁项目集的项目删掉for i in N:for j in Ck:if set(i).issubset(j):Ck.remove(j)                   return Ck# Apriori算法 逐层迭代
def apriori(D,minSupport):C1 = createCl(D)L1,N,supportData = scanD(D,C1,minSupport)L=[L1]k=2while (len(L[k-2]) > 0):Ck = aprioriGen(L[k-2],k,N)Lk,Nk,supK = scanD(D,Ck,minSupport)supportData.update(supK)N += NkL.append(Lk)k +=1return L,N,supportData

Apriori 算法改进

Apriori 仍可能产生大量的候选集

​ Apriori 算法虽然通过剪枝在很大程度上压缩了候选项集集合，但是在逐层迭代搜索过程中，如果要生成一个很长的规则，这将产生大量的中间元素，仍然会产生大量的候选集，需要大量的计算和存储资源。

使用哈希函数生成候选集

​ 在基于 𝐿𝑘−1生成候选项集集合 𝐶𝑘时，直接使用哈希函数生成候选项集，达到压缩候选项集目的。
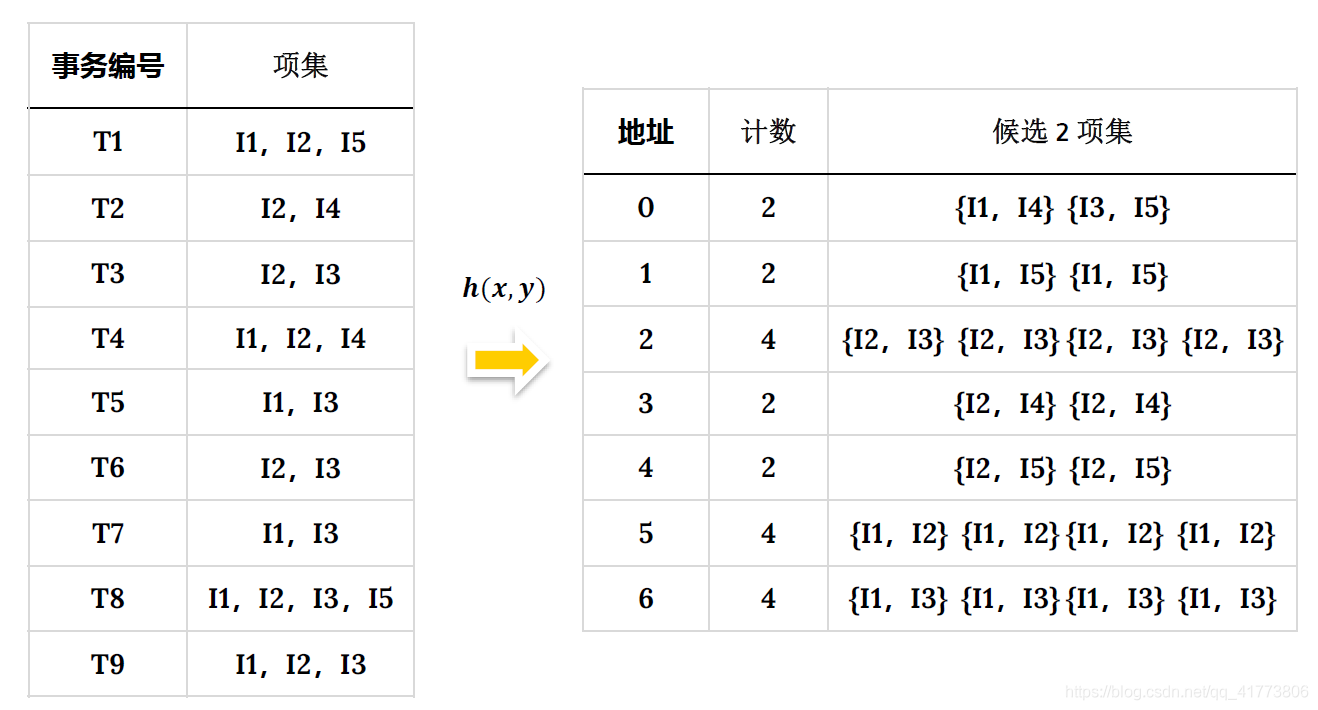
​ 例如上述 Apriori 实例中由 𝐿1生成候选项集集合 𝐶2 时，使用如下哈希函数创建哈希表：
$$h(x,y)=(10x+y)mod7$$
​ 如果预设最小支持度计数为 3 ，则哈希地址为 0 、 1 、 3 、 4 中的候选项集都不可能是频繁的直接被剔除。

频繁模式增长算法 FP-growth

​ FP-growth 算法直接避免了繁杂而开销巨大的候选项集生成过程，采用如下分治策略：
​ (1) 首先，将代表频繁项集的数据库压缩到一棵频繁模式树 FP-Tree
​ (2) 然后，把这种压缩后的数据库划分成一组条件数据库 ，每个数据库关联一个频繁项或模式段，并分别挖掘每个条件数据库。对于每个模式段只需要考察与它相关联的数据集。随着被考察模式的增长，这种方法可以显著地压缩被搜索的数据集大小。

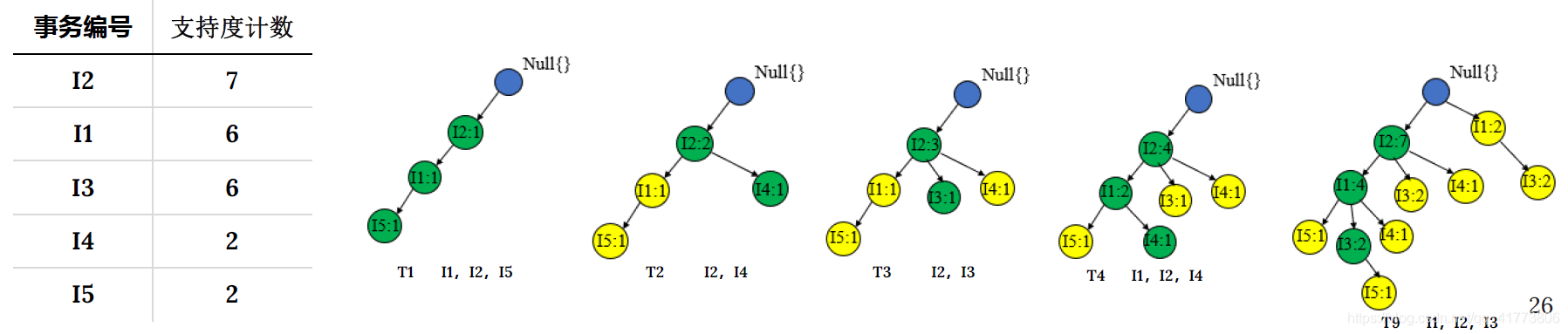
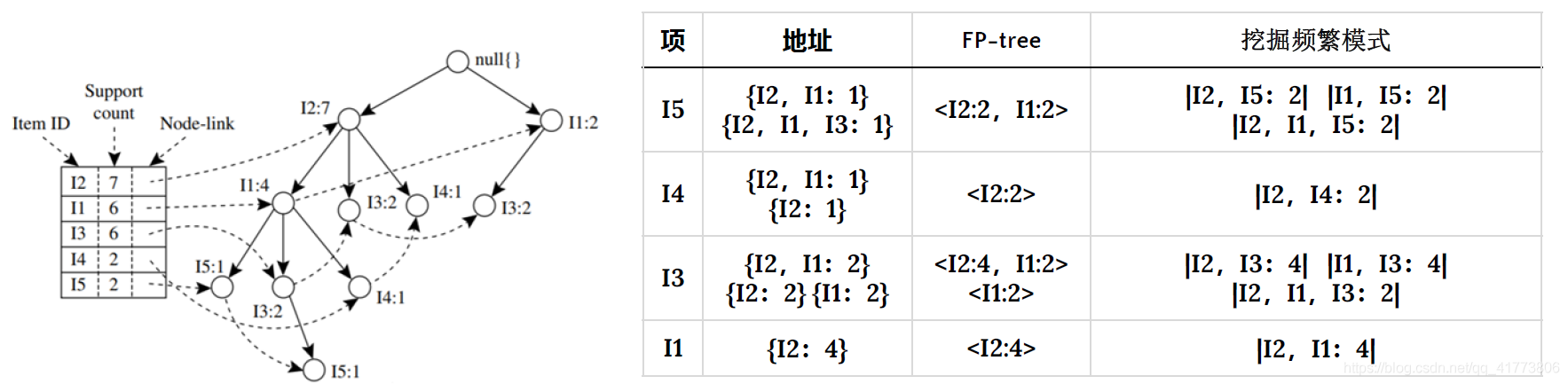
1. 构造频繁模式树 FP-tree ：首先，导出频繁 1 项集集合 𝐿，且将该频繁 1 项集集合按支持度计数降序排序 。然后，依据 𝐿构造频繁模式树，先创建树的根节点，用 null 标记；接着扫描数据库，将每个事务的项集中的项按 𝐿 的次序创建节点，并对每一个事物创建一个分枝。

2. 从FP-tree中挖掘频繁模式：从初始后缀模式即长度为1 的频繁模式开始挖掘，构造一个由 FP-tree 中与该后缀模式一起出现的前缀路径集组成的子数据库，称为该频繁模式的条件模式基。然后，构造该频繁模式的条件 FP-tree ，并递归地在该树上挖掘频繁模式。模式增长通过后缀模式与条件FP-tree产生的频繁模式连接实现。

Apriori 会产生大量虚假的关联规则

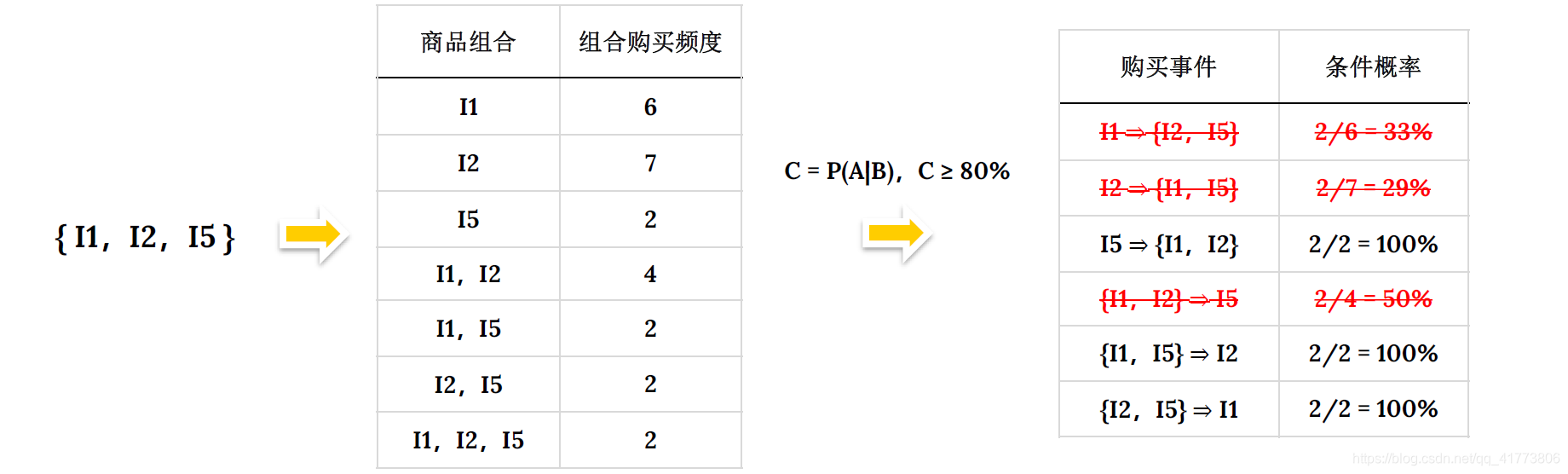
​ Apriori 算法衡量和生成关联规则的标准主要有两个，即支持度和置信度。但仅用这两个标准来衡量关联规则，往往会发现大量冗余的、虚假的关联规则。例如，有 10 个购物事物中有 6 个包含购买可口可乐的事物，有 7 个包含购买百事可乐的事务，同时包含购买可口可乐和百事可乐的事务有 4 个。预设最小支持度为 30%，最小置信度为 60%，使用 Apriori 算法可以得到如下关联规则：

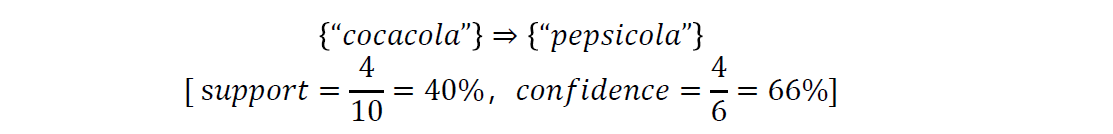
​ 事实上可口可乐和百事可乐的购买事务是负相关的，买一种会降低另一种被购买的可能性，所以这个关联规则是虚假的。

​ 可以看出仅仅使用支持度和置信度不足以过滤掉冗余的和虚假的关联规则。为此，可以使用相关性度量来扩充关联规则的支持度-置信度框架。加入了相关性度量的关联规则称为相关规则用如下形式表示：
$$A=>B[support,confidence,correlation]$$
​ 常用的相关性度量由：

1. 提升度：提升度是一种简单的相关性度量，如果值小于 1 表示 A 的出现和 B 的出现是负相关的，如果值大于 1 表示两者是正相关的，如果值等于 1 表示 A 和 B 是独立的，两者不具有相关性 。

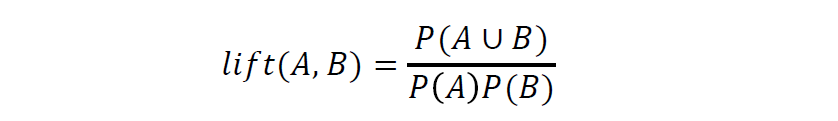
2. 卡方检验：卡方检验也可以用于相关性度量通过表示实际观测值 (𝑎)与理论推断值 (𝑝)之间的偏离程度即卡方值大小来表示相关性 。 如果卡方值越大二者偏差程度越大呈负相关，反之二者偏差越小呈正相关，若两个值完全相等时，卡方值就为 0 表明理论值完全符合 表示事件互相独立 。

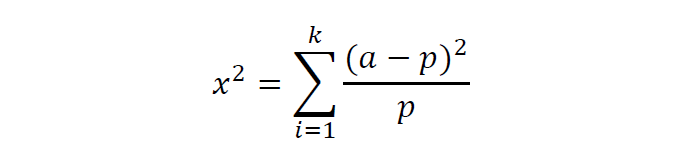
Apriori 对稀有信息分析效果差

​ Apriori 的频繁项集挖掘是基于最小支持度实现的，然而可能有一些有价值的规则的支持度小于这一预设的最小支持度或由于数据量较少无法正确生成相关规则。对于这种数据不平衡的情况，需要尽量减少事务总数的评估影响。

​ 零事务，提升度和卡方检验都受到被分析事务总数的影响，例如有102100 个事务中，可口可乐百事可乐被同时购买的事务有 100 个，可口可乐被单独购买的事务 1000 个，百事可乐被单独购买的事务有 1000 个。这个数据计算出来的提升度和卡方值都出现正关联错误评估。这是由大量的不包含那些考查项集的事务影响造成的，这些事务称为零事务 。实际情况中零事务的个数往往比被考察事务个数大很多。

​ 可以使用不平衡比来评估两个项集的不平衡程度，不平衡比值越大说明两个项集不平衡情况严重，若不平衡比值为 0 说明其平衡情况较好 ，计算公式如下：

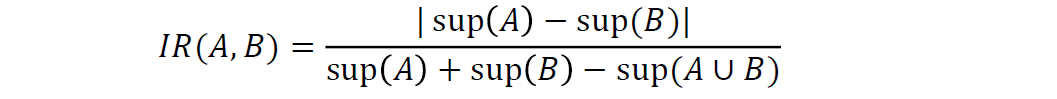
​ 常用的零不变性度量如下所示：

完整Apriori算法 PPT 和 Python 实现代码下载地址：下载地址