1 案例背景

购物篮分析是通过发现顾客在一次购买行为中放入购物篮中不同商品之间的关联，研究顾客的购买行为，从而辅助零售企业制定营销策略的一种数据分析方法。
通过对商场销售数据进行分析，得到顾客的购买行为特征，并根据发现的规律而采取有效的行动，制定商品摆放、商品定价、新商品采购计划，对增加销量并获取最大利润有重要意义。
本案例使用Apriori关联规则算法实现购物篮分析，发现超市不同商品之间的关联关系，并根据商品之间的关联规则制定销售策略。

2 目标

• 构建零售商品的Apriori关联规则模型，分析商品之间的关联性。
• 根据模型结果给出销售策略。

3 分析方法

购物篮关联规则挖掘的主要步骤如下：

(1) 对原始数据进行数据探索性分析，分析商品的热销情况与商品结构。
(2) 对原始数据进行数据预处理，转换数据形式，使之符合Apriori关联规则算法要求。
(3) 在步骤2得到的建模数据基础上，采用Apriori关联规则算法调整模型输入参数，完成商品关联性分析。
(4) 结合实际业务，对模型结果进行分析，根据分析结果给出销售建议，最后输出关联规则结果。

4 数据探索分析

查看数据特征以及对商品热销情况和商品结构进行分析

4.1 数据特征

%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as pltplt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = Falsedata =pd.read_csv('./data/GoodsOrder.csv',encoding = 'gbk')
data.info()  # 查看数据属性
print("-"*40)print('描述性统计结果：\n',data.describe().T)  
# 输出结果
'''
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 43367 entries, 0 to 43366
Data columns (total 2 columns):
id       43367 non-null int64
Goods    43367 non-null object
dtypes: int64(1), object(1)
memory usage: 677.7+ KB
----------------------------------------
描述性统计结果：count         mean          std  min     25%     50%     75%     max
id  43367.0  4908.589504  2843.118248  1.0  2455.5  4828.0  7380.5  9835.0
'''

4.2 分析热销商品

销量排行前10商品的销量及其占比

# 对商品进行分类汇总
Top10 = data.groupby(['Goods']).count().reset_index()  
Top10 = Top10.sort_values('id',ascending=False)x = Top10[:10]['Goods'][::-1]
y = Top10[:10]['id'][::-1]
plt.figure(figsize=(18,12), dpi=80)
plt.barh(x, y, height=0.5, color='#6699CC')
plt.xlabel('销量',size=16)
plt.ylabel('商品类别',size=16) 
plt.title('商品的销量TOP10', size=24)
plt.xticks(size=16) # x轴字体大小调整
plt.yticks(size=16) # y轴字体大小调整
plt.show()

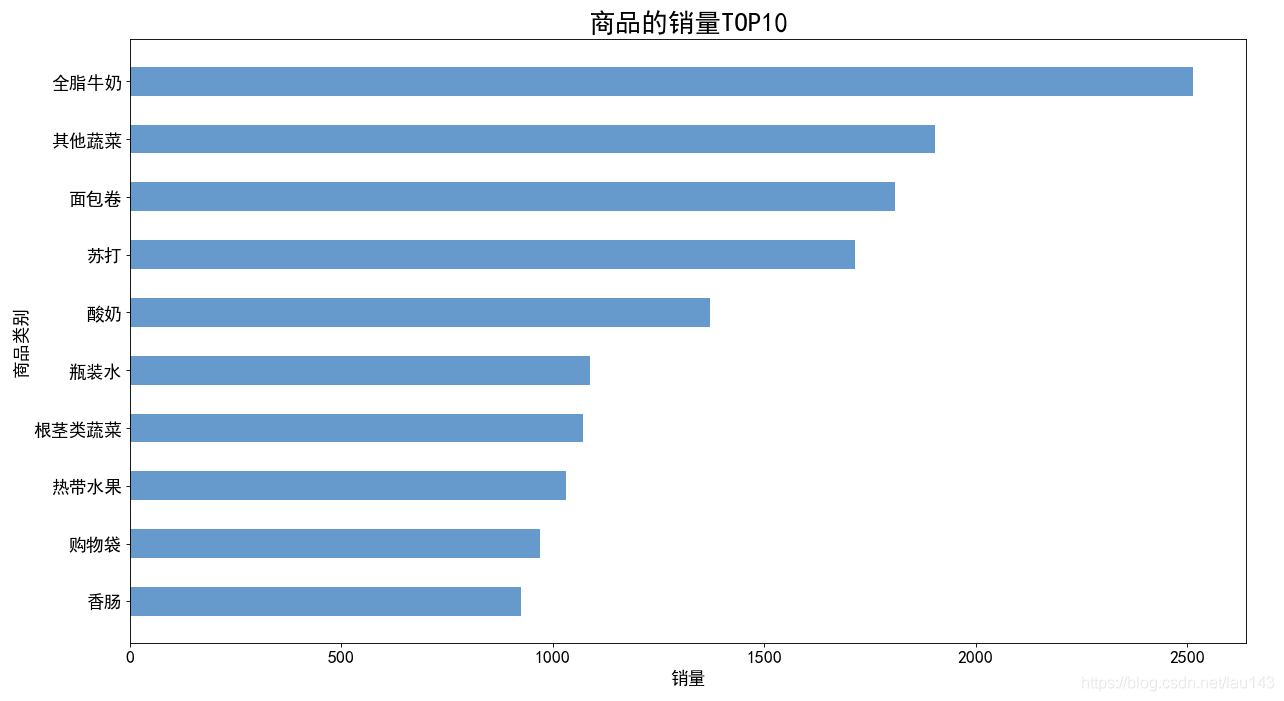
销量排行前10商品的销量占比

# 销量排行前10商品的销量占比
data_nums = data.shape[0]
for index, row in Top10[:10].iterrows():print(row['Goods'],row['id'],row['id']/data_nums)'''
全脂牛奶 2513 0.25551601423487547
其他蔬菜 1903 0.1934926283680732
面包卷 1809 0.18393492628368074
苏打 1715 0.17437722419928825
酸奶 1372 0.13950177935943062
瓶装水 1087 0.11052364006100661
根茎类蔬菜 1072 0.10899847483477376
热带水果 1032 0.10493136756481952
购物袋 969 0.09852567361464158
香肠 924 0.09395017793594305
'''

各类别商品的销量及其占比

inputfile1 = './data/GoodsOrder.csv'
inputfile2 = './data/GoodsTypes.csv'# 读入数据
data = pd.read_csv(inputfile1,encoding = 'gbk')
types = pd.read_csv(inputfile2,encoding = 'gbk') group = data.groupby(['Goods']).count().reset_index()
sort = group.sort_values('id',ascending = False).reset_index()data_nums = data.shape[0]  # 总量
del sort['index']# 合并两个datafreame,on='Goods'
sort_links = pd.merge(sort,types)# 根据类别求和，每个商品类别的总量，并排序
sort_link = sort_links.groupby(['Types']).sum().reset_index()
sort_link = sort_link.sort_values('id',ascending = False).reset_index()
del sort_link['index']  # 删除“index”列# 求百分比，然后更换列名，最后输出到文件
sort_link['count'] = sort_link.apply(lambda line: line['id']/data_nums,axis=1)
sort_link.rename(columns = {'count':'percent'},inplace = True)
print('各类别商品的销量及其占比:\n',sort_link)# 保存结果
outfile1 = './percent.csv'
sort_link.to_csv(outfile1,index = False,header = True,encoding='gbk')'''
各类别商品的销量及其占比:Types    id   percent
0  非酒精饮料  7594  0.175110
1     西点  7192  0.165840
2     果蔬  7146  0.164780
3   米粮调料  5185  0.119561
4     百货  5141  0.118546
5     肉类  4870  0.112297
6   酒精饮料  2287  0.052736
7    食品类  1870  0.043120
8     零食  1459  0.033643
9     熟食   541  0.012475
'''

每类商品销量占比

data = sort_link['percent']
labels = sort_link['Types']
plt.figure(figsize=(7, 7))
plt.pie(data,labels=labels,autopct='%1.2f%%',startangle=90)
plt.title('每类商品销量占比')
# plt.savefig('./persent.png')  # 把图片以.png格式保存
plt.show()

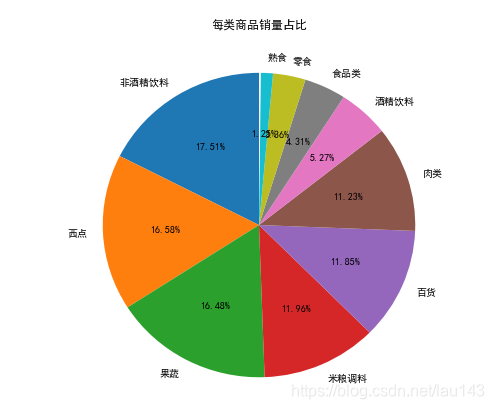
分析：
通过分析各类别商品的销量及其占比情况可知，非酒精饮料、西点、果蔬3类商品的销量差距不大，占总销量的50%左右。

进一步查看销量第一的非酒精饮料类商品的内部商品结构，并绘制饼图显示其销量占比情况

# 先筛选“非酒精饮料”类型的商品，然后求百分比，然后输出结果到文件。
selected = sort_links.loc[sort_links['Types'] == '非酒精饮料']
# 对所有的“非酒精饮料”求和
child_nums = selected['id'].sum()
# 求百分比
selected.loc[:,'child_percent'] = selected.apply(lambda line: line['id']/child_nums,axis = 1)
selected.rename(columns = {'id':'count'},inplace = True)
print('非酒精饮料内部商品的销量及其占比:\n',selected)
outfile2 = './child_percent.csv'
sort_link.to_csv(outfile2,index = False,header = True,encoding='gbk')  # 输出结果'''
非酒精饮料内部商品的销量及其占比:Goods  count  Types  child_percent
0        全脂牛奶   2513  非酒精饮料       0.330919
3          苏打   1715  非酒精饮料       0.225836
5         瓶装水   1087  非酒精饮料       0.143139
16     水果/蔬菜汁    711  非酒精饮料       0.093627
22         咖啡    571  非酒精饮料       0.075191
38   超高温杀菌的牛奶    329  非酒精饮料       0.043324
45       其他饮料    279  非酒精饮料       0.036740
51       一般饮料    256  非酒精饮料       0.033711
101      速溶咖啡     73  非酒精饮料       0.009613
125         茶     38  非酒精饮料       0.005004
144      可可饮料     22  非酒精饮料       0.002897
'''

展示非酒精饮品内部各商品的销量占比

data = selected['child_percent']
labels = selected['Goods']plt.figure(figsize = (8,6))
# 设置每一块分割出的间隙大小
explode = (0.02,0.03,0.04,0.05,0.06,0.07,0.08,0.08,0.3,0.1,0.3)
plt.pie(data,explode = explode,labels = labels,autopct = '%1.2f%%',pctdistance = 1.1,labeldistance = 1.2)
# 设置标题
plt.title("非酒精饮料内部各商品的销量占比")
# 把单位长度都变的一样
plt.axis('equal')# 保存图形
# plt.savefig('./child_persent.png')
plt.show()

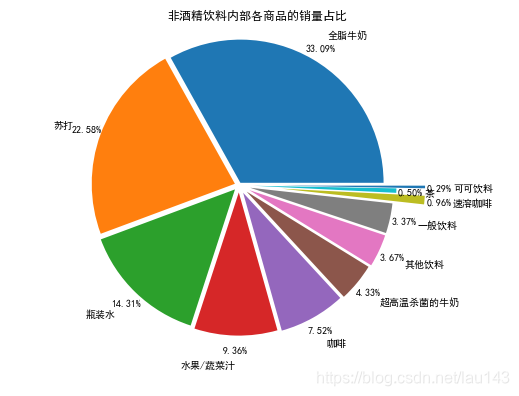
分析：
通过分析非酒精饮料内部商品的销量及其占比情况可知，全脂牛奶的销量在非酒精饮料的总销量中占比超过33%，前3种非酒精饮料的销量在非酒精饮料的总销量中的占比接近70%，这就说明大部分顾客到店购买的饮料为这3种，而商场就需要时常注意货物的库存，定期补货。

5 数据预处理

前面对数据探索分析发现数据完整，并不存在缺失值。建模之前需要转变数据的格式，才能使用Apriori函数进行关联分析。这里对数据进行转换。

inputfile = 'data/GoodsOrder.csv'
data = pd.read_csv(inputfile,encoding = 'gbk')# 根据id对“Goods”列合并，并使用“，”将各商品隔开
data['Goods'] = data['Goods'].apply(lambda x:','+x)
data = data.groupby('id').sum().reset_index()# 对合并的商品列转换数据格式
data['Goods'] = data['Goods'].apply(lambda x :[x[1:]])
data_list = list(data['Goods'])# 分割商品名为每个元素
data_translation = []
for i in data_list:p = i[0].split(',')data_translation.append(p)
print('数据转换结果的前5个元素：\n', data_translation[0:5])'''
数据转换结果的前5个元素：[['柑橘类水果', '人造黄油', '即食汤', '半成品面包'], ['咖啡', '热带水果', '酸奶'], ['全脂牛奶'], ['奶油乳酪', '肉泥', '仁果类水果', '酸奶'], ['炼乳', '长面包', '其他蔬菜', '全脂牛奶']]
'''

6 模型构建

本案例的目标是探索商品之间的关联关系，因此采用关联规则算法，以挖掘它们之间的关联关系。关联规则算法主要用于寻找数据中项集之间的关联关系，它揭示了数据项间的未知关系。基于样本的统计规律，进行关联规则分析。根据所分析的关联关系，可通过一个属性的信息来推断另一个属性的信息。当置信度达到某一阈值时，就可以认为规则成立。

Apriori算法是常用的关联规则算法之一，也是最为经典的分析频繁项集的算法，它是第一次实现在大数据集上可行的关联规则提取的算法。除此之外，还有FP-Tree算法，Eclat算法和灰色关联算法等。本案例主要使用Apriori算法进行分析。

模型具体实现步骤:

• 设置建模参数最小支持度、最小置信度，输入建模样本数据
• 采用Apriori关联规则算法对建模的样本数据进行分析，以模型参数设置的最小支持度、最小置信度以及分析目标作为条件，如果所有的规则都不满足条件，则需要重新调整模型参数，否则输出关联规则结果。

目前，如何设置最小支持度与最小置信度并没有统一的标准。大部分都是根据业务经验设置初始值，然后经过多次调整，获取与业务相符的关联规则结果。本案例经过多次调整并结合实际业务分析，选取模型的输入参数为：最小支持度0.02、最小置信度0.35。其关联规则代码如代码所示。

from numpy import *def loadDataSet():return [['a', 'c', 'e'], ['b', 'd'], ['b', 'c'], ['a', 'b', 'c', 'd'], ['a', 'b'], ['b', 'c'], ['a', 'b'],['a', 'b', 'c', 'e'], ['a', 'b', 'c'], ['a', 'c', 'e']]def createC1(dataSet):C1 = []for transaction in dataSet:for item in transaction:if not [item] in C1:C1.append([item])C1.sort()# 映射为frozenset唯一性的，可使用其构造字典return list(map(frozenset, C1))   # 从候选K项集到频繁K项集（支持度计算）
def scanD(D, Ck, minSupport):ssCnt = {}for tid in D:   # 遍历数据集for can in Ck:  # 遍历候选项if can.issubset(tid):  # 判断候选项中是否含数据集的各项if not can in ssCnt:ssCnt[can] = 1  # 不含设为1else:ssCnt[can] += 1  # 有则计数加1numItems = float(len(D))  # 数据集大小retList = []  # L1初始化supportData = {}  # 记录候选项中各个数据的支持度for key in ssCnt:support = ssCnt[key] / numItems  # 计算支持度if support >= minSupport:retList.insert(0, key)  # 满足条件加入L1中supportData[key] = support  return retList, supportDatadef calSupport(D, Ck, min_support):dict_sup = {}for i in D:for j in Ck:if j.issubset(i):if not j in dict_sup:dict_sup[j] = 1else:dict_sup[j] += 1sumCount = float(len(D))supportData = {}relist = []for i in dict_sup:temp_sup = dict_sup[i] / sumCountif temp_sup >= min_support:relist.append(i)# 此处可设置返回全部的支持度数据（或者频繁项集的支持度数据）supportData[i] = temp_supreturn relist, supportData# 改进剪枝算法
def aprioriGen(Lk, k):retList = []lenLk = len(Lk)for i in range(lenLk):for j in range(i + 1, lenLk):  # 两两组合遍历L1 = list(Lk[i])[:k - 2]L2 = list(Lk[j])[:k - 2]L1.sort()L2.sort()if L1 == L2:  # 前k-1项相等，则可相乘，这样可防止重复项出现# 进行剪枝（a1为k项集中的一个元素，b为它的所有k-1项子集）a = Lk[i] | Lk[j]  # a为frozenset()集合a1 = list(a)b = []# 遍历取出每一个元素，转换为set，依次从a1中剔除该元素，并加入到b中for q in range(len(a1)):t = [a1[q]]tt = frozenset(set(a1) - set(t))b.append(tt)t = 0for w in b:# 当b（即所有k-1项子集）都是Lk（频繁的）的子集，则保留，否则删除。if w in Lk:t += 1if t == len(b):retList.append(b[0] | b[1])return retListdef apriori(dataSet, minSupport=0.2):
# 前3条语句是对计算查找单个元素中的频繁项集C1 = createC1(dataSet)D = list(map(set, dataSet))  # 使用list()转换为列表L1, supportData = calSupport(D, C1, minSupport)L = [L1]  # 加列表框，使得1项集为一个单独元素k = 2while (len(L[k - 2]) > 0):  # 是否还有候选集Ck = aprioriGen(L[k - 2], k)Lk, supK = scanD(D, Ck, minSupport)  # scan DB to get LksupportData.update(supK)  # 把supk的键值对添加到supportData里L.append(Lk)  # L最后一个值为空集k += 1del L[-1]  # 删除最后一个空集return L, supportData  # L为频繁项集，为一个列表，1，2，3项集分别为一个元素# 生成集合的所有子集
def getSubset(fromList, toList):for i in range(len(fromList)):t = [fromList[i]]tt = frozenset(set(fromList) - set(t))if not tt in toList:toList.append(tt)tt = list(tt)if len(tt) > 1:getSubset(tt, toList)def calcConf(freqSet, H, supportData, ruleList, minConf=0.7):for conseq in H:  #遍历H中的所有项集并计算它们的可信度值conf = supportData[freqSet] / supportData[freqSet - conseq]  # 可信度计算，结合支持度数据# 提升度lift计算lift = p(a & b) / p(a)*p(b)lift = supportData[freqSet] / (supportData[conseq] * supportData[freqSet - conseq])if conf >= minConf and lift > 1:print(freqSet - conseq, '-->', conseq, '支持度', round(supportData[freqSet], 6), '置信度：', round(conf, 6),'lift值为：', round(lift, 6))ruleList.append((freqSet - conseq, conseq, conf))# 生成规则
def gen_rule(L, supportData, minConf = 0.7):bigRuleList = []for i in range(1, len(L)):  # 从二项集开始计算for freqSet in L[i]:  # freqSet为所有的k项集# 求该三项集的所有非空子集，1项集，2项集，直到k-1项集，用H1表示，为list类型,里面为frozenset类型，H1 = list(freqSet)all_subset = []getSubset(H1, all_subset)  # 生成所有的子集calcConf(freqSet, all_subset, supportData, bigRuleList, minConf)return bigRuleListif __name__ == '__main__':dataSet = data_translationL, supportData = apriori(dataSet, minSupport = 0.02)rule = gen_rule(L, supportData, minConf = 0.35)

根据输出结果，对其中4条进行解释分析如下：

• {‘其他蔬菜’，‘酸奶’}=>{‘全脂牛奶’}支持度约为2.23%，置信度约为51.29%。说明同时购买酸奶、其他蔬菜和全脂牛奶这3种商品的概率达51.29%，而这种情况发生的可能性约为2.23%。
• {‘其他蔬菜’}=>{‘全脂牛奶’}支持度最大约为7.48%，置信度约为38.68%。说明同时购买其他蔬菜和全脂牛奶这两种商品的概率达38.68%，而这种情况发生的可能性约为7.48%。
• {‘根茎类蔬菜’}=>{‘全脂牛奶’}支持度约为4.89%，置信度约为44.87%。说明同时购买根茎类蔬菜和全脂牛奶这3种商品的概率达44.87%，而这种情况发生的可能性约为4.89%。
• {‘根茎类蔬菜’}=>{‘其他蔬菜’}支持度约为4.74%，置信度约为43.47%。说明同时购买根茎类蔬菜和其他蔬菜这两种商品的概率达43.47%，而这种情况发生的可能性约为4.74%。

由上分析可知，顾客购买酸奶和其他蔬菜的时候会同时购买全脂牛奶，其置信度最大达到51.29%。因此，顾客同时购买其他蔬菜、根茎类蔬菜和全脂牛奶的概率较高。

对于模型结果，从购物者角度进行分析：现代生活中，大多数购物者为“家庭煮妇”，购买的商品大部分是食品，随着生活质量的提高和健康意识的增加，其他蔬菜、根茎类蔬菜和全脂牛奶均为现代家庭每日饮食的所需品。因此，其他蔬菜、根茎类蔬菜和全脂牛奶同时购买的概率较高，符合人们的现代生活健康意识。

7 模型应用

模型结果表明：顾客购买其他商品的时候会同时购买全脂牛奶。因此，商场应该根据实际情况将全脂牛奶放在顾客购买商品的必经之路上，或是放在商场显眼的位置，以方便顾客拿取。顾客同时购买其他蔬菜、根茎类蔬菜、酸奶油、猪肉、黄油、本地蛋类和多种水果的概率较高，因此商场可以考虑捆绑销售，或者适当调整商场布置，将这些商品的距离尽量拉近，从而提升顾客的购物体验。