一、实验目的
- 掌握对数据进行预处理和探索性分析的方法;
- 掌握如何利用Apriori关联规则算法进行购物篮分析。
二实验内容
- 构建零售商品的Apriori关联规则模型,分析商品之间的关联性;
- 根据模型结果给出销售策略。
三、实验操作步骤和结果分析
首先导入需要用到的库
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt加载数据集
# 加载数据
order_data = pd.read_csv("GoodsOrder.csv")
types_data = pd.read_csv("GoodsTypes.csv")查看原始数据集的缺失值情况
# 原始数据集缺失值情况。
print("GoodsOrder数据的缺失值情况:\n",order_data.isnull().sum())
print("GoodsTypes数据的缺失情况:\n",types_data.isnull().sum())运行截图:

查看数据形状
# 数据形状
print("GoodsOrder表形状:",order_data.shape)
print("GoodsTypes表形状:",types_data.shape)运行截图:

绘制销量前十的商品柱状图
# 统计销量前10的商品
# 按照Goods列进行分组然后计数,并重新设置索引。
group = data1.groupby(['Goods']).count().reset_index()
print("group:\n",group)
# 按照id进行降序排列
sort = group.sort_values(by='id',ascending = False).reset_index(drop=True)
print("sort:\n",sort)plt.rcParams['font.sans-serif'] = ['SimHei'] # 设置图形里面中文为黑体
# 绘制销量前10的商品数理统计图
plt.figure(figsize=(8, 5))
sns.barplot(x=sort.iloc[:10,0],y=sort.iloc[:10,1])
plt.ylabel('商品销量',fontsize=15)
plt.xlabel('商品类别',fontsize=15)
plt.title('销量排名前10的商品销量情况',fontsize=20)
绘制销量前十商品的占比折线图
# 销量前十的商品销量占比统计图
plt.figure(figsize=(8, 5))
plt.plot(sort.iloc[:10, 0], part)
plt.title("销量前十的商品占比折线图", fontsize=20)
plt.xlabel("商品类别", fontsize=14)
plt.ylabel("比率", fontsize=14)

绘制销量最后10位的商品数量统计图
plt.figure(figsize=(8,5))
# plt.plot(sort.iloc[-10:, 0],sort.iloc[-10:, 1]) # 绘制折线图
sns.barplot(x=sort.iloc[-10:, 1],y=sort.iloc[-10:, 0])
plt.xlabel("商品销量")
plt.ylabel("商品类别")
plt.title("销量排名最后10位的商品销量情况",fontsize=20)
统计每个商品类别的销量及占比
#
type_count = outer.groupby("Types").count().reset_index()
type_count["rate"] = type_count["Goods"]/len(data1) # 计算商品类别销量占比
type_count.sort_values("id",ascending=False,inplace=True) # 对销量进行降序排序
print(type_count)# 绘制每个商品类别的销量占比饼状图
plt.figure(figsize=(6,5))
plt.pie(x=type_count["rate"],labels=type_count["Types"],autopct='%1.2f%%',labeldistance=1.05)
plt.axis('equal') # 显示为圆(避免比例压缩为椭圆)
plt.title('不同商品类型销量占比',fontsize=15)
绘制每个商品类别的销量占比饼状图
#
plt.figure(figsize=(6,5))
plt.pie(x=type_count["rate"],labels=type_count["Types"],autopct='%1.2f%%',labeldistance=1.05)
plt.axis('equal') # 显示为圆(避免比例压缩为椭圆)
plt.title('不同商品类型销量占比',fontsize=15)
# 绘制非酒精饮料类别中不同商品占比的条形图
plt.figure(figsize=(10, 5))
sns.barplot(x=list(drink["id"]), y=list(drink["Goods"]))
plt.title("非酒精饮料类别中不同商品的销量", fontsize= 15)
plt.xlabel("商品销量")
plt.ylabel("商品类别")
# 西点
pastry = outer[outer["Types"] == "西点"].groupby("Goods").count().reset_index()
# 绘制西点类别中不同商品占比的条形图
plt.figure(figsize=(10, 5))
sns.barplot(x=list(pastry["id"]), y=list(pastry["Goods"]))
plt.title("西点类别中不同商品的销量", fontsize= 15)
plt.xlabel("商品销量")
plt.ylabel("商品类别")
# 果蔬
pastry = outer[outer["Types"] == "果蔬"].groupby("Goods").count().reset_index()
# 绘制果蔬类别中不同商品占比的条形图
plt.figure(figsize=(10, 5))
sns.barplot(x=list(pastry["id"]), y=list(pastry["Goods"]))
plt.title("果蔬类别中不同商品的销量", fontsize= 15)
plt.xlabel("商品销量")
plt.ylabel("商品类别")plt.show()
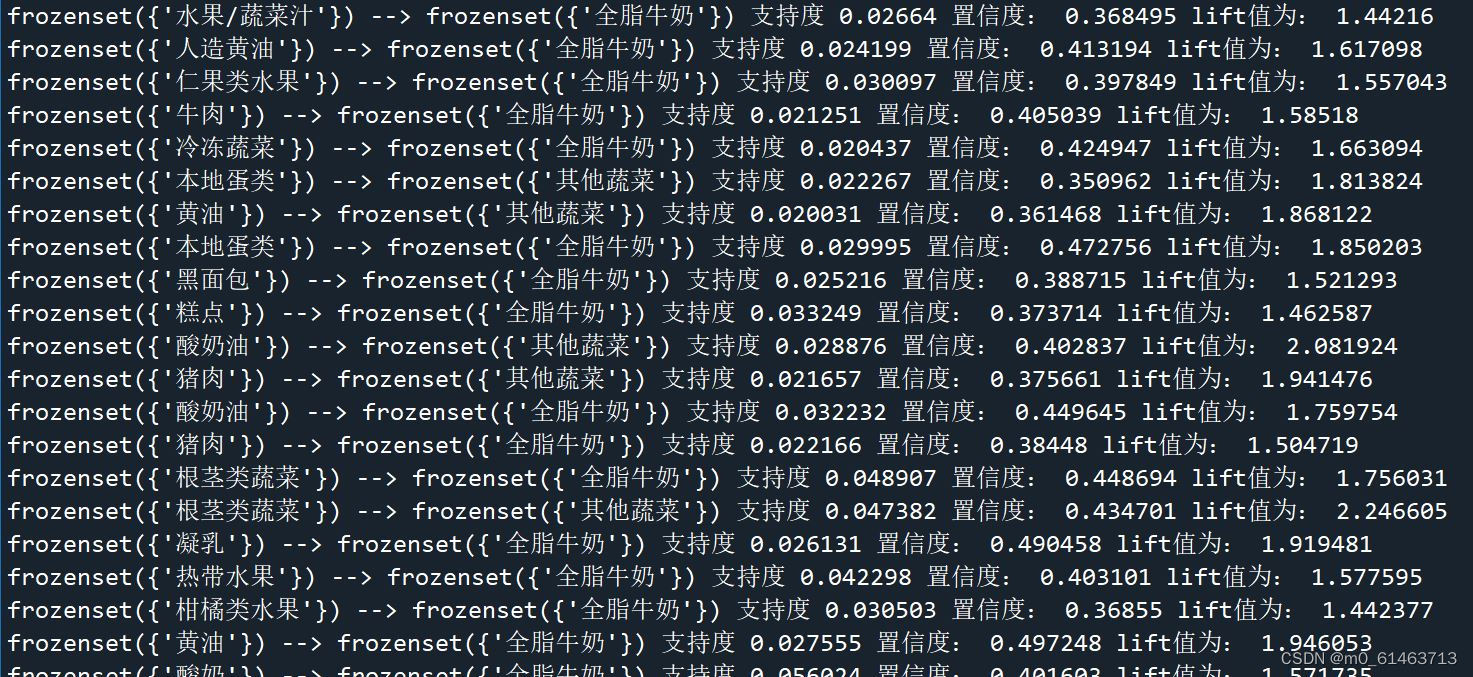
通过不断的修改最小支持度和置信度,最终综合考虑不同的结果,我将最小支持度设为0.02,最小置信度设置为0.3,得到122个支持度大于0.02的频繁项集。37个关联规则,如下图所示。


保存到csv文件中的强关联规则:

(三) 手动实现Apriori算法
- 伪代码
# 找出频繁 1 项集 L1 =find_frequent_1 - itemsets(D); For(k=2; !=Null; k++){
# 产生候选,并剪枝 = Apriori_gen(Lk-1);
# 扫描 D 进行候选计数 For each 事务t in D{ =subset( , t); # 得到 t 的子集 For each 候选 c 属于 c.count++; } # 返回候选项集中不小于最小支持度的项集 ={
c 属于 | c.count>=min_sup
}
}
Return L= 所有的频繁集; 连接(join)
Procedure Apriori_gen ( : frequent(k-1)-itemsets) For each 项集 属于 For each 项集 属于 If( ( [1]= [1])&&( [2]= [2])&& ……&&( [k-2]= [k-2])&&( [k-1]< [k-1]) )
then{ c = 连接 # 连接步:产生候选 # 若k-1项集中已经存在子集c则进行剪枝 if has_infrequent_subset(c, ) then delete c; # 剪枝步:删除非频繁候选 else add c to ; } Return ; 剪枝
Procedure has_infrequent_sub (c: candidate k-itemset; : frequent(k-1)-itemsets) For each (k-1)-subset s of c If s 不属于 then Return true; Return false; - 手敲Apriori算法代码
def DealData(): # 数据预处理Order_data = pd.read_csv("GoodsOrder.csv")# 遍历每一个商品名,在其后面加上一个空格,便于合并每一张订单中的所有商品Order_data["Goods"] = Order_data["Goods"].map(lambda x : x+" ")Order_data = Order_data.groupby("id").sum().reset_index()# print(Order_data)# 将每一张订单中的每一个商品提取出来Order_data["Goods"] = Order_data["Goods"].map(lambda x:x.strip().split(" "))order = list(Order_data["Goods"])# print(order)return order
def findOneSet(data):"""计算1项候选集C1:param data: 数据集:return: 1项候选集"""C1 = []for i in data: # i为每一行的数据for j in i: # j为每一列的数据,即一张订单中的单个商品元素if [j] not in C1:C1.append([j])C1 = list(map(frozenset, C1)) # 将集合C1冻结,不能添加或者删除元素。return C1
def CalculateSupport(data, C, min_support):"""计算1项候选集的支持度,剔除不满足最小支持度的项集:param data::param C::param min_support: 最小支持度:return: 频繁1项集及其支持度"""dict_c = dict() # 存储中间值,用于计数# 统计项集中的每一项元素for i in data:for j in C:if j.issubset(i): # 判断j是否为i的子集if j not in dict_c: # 判断是否统计过该元素dict_c[j] = 1 # 没有统计过就初始化为1else:dict_c[j] += 1sumc = float(len(data)) # 事务的总数# 计算支持度sd = dict() # 用于存放频繁集的支持度listc = [] # 存放频繁项集for i in dict_c:t = dict_c[i] /sumc # 计算支持度,临时存放# 存下满足最小支持度的频繁项集if t > min_support:listc.append(i) # 添加评频繁1项集sd[i] = t # 存入支持度return listc, sd # 返回频繁一项集和支持度
def AprioriGenerate(lk, k):"""利用剪枝算法,找出k项候选集:param lk: 频繁k-1项集:param k: 第k项:return: 第k项候选集"""listk = [] # 存放第k项候选集length_lk = len(lk) # 第k-1项频繁集的长度# 两两组合for i in range(length_lk):for j in range(i+1, length_lk):l1 = list(lk[i])[:k-2]l2 = list(lk[j])[:k-2]l1.sort()l2.sort()#前k-1项相等,就可以相乘,从而防止重复项出现if l1 == l2:s = lk[i] | lk[j] # s是被冻结的集合,不能增加删除元素# 进行剪枝s1 = list(s)son = [] # 她的所有k-1项子集# 构造son,遍历每一个商品元素,转换成集合set,依次从s1中删除该元素,并加入到son中for x in range(len(s1)):t = [s1[x]]t1 = frozenset(set(s1)- set(t))son.append(t1)# 当son都是频繁项集时,保留s1c = 0for r in son:if r in lk: # 判断是否属于候选集c += 1# 所有子集都是候选集则其自身为候选集if len(son) == c:listk.append(son[0] | son[1])return listk
def scanData(data, Ck, min_support):"""计算候选k项集的支持度,找出满足最小支持度的频繁k项集及其支持度:param data: 数据集:param Ck: 候选k项集:param min_support 最小支持度::return: 返回频繁k项集"""dicts = dict() # 存放支持度for i in data:for j in Ck:if j.issubset(i):if j not in dicts:dicts[j] = 1else:dicts[j] += 1# 计算支持度sumi = len(data) # 事务总数listck = [] # 存放频繁k项集sd = dict() # 存放频繁集的支持度for q in dicts:s = dicts[q] / sumiif s > min_support: # 判段支持度是否满足最小支持度listck.insert(0, q)sd[q] = s# 返回频繁k项集和其支持度return listck, sd
def Apriori(data, min_support=0.1):"""Apriori关联规整算法:param data: 数据集:param min_support: 最小支持度:return: 频繁项集和支持度"""global frequentItem# 先找到1项候选集C1 = findOneSet(data)# 将数据转换成列表,方便计算支持度data = list(map(set,data))# 计算1项候选集的支持度,找到满足最小支持度的项集l1, support_data = CalculateSupport(data, C1, min_support)l = [l1] #添加到列表之中,使得1项频繁集成一个单独的元素k = 2 # k项while len(l[k-2]) > 0: # 循环直到没有候选集结束# 产生k项候选集CkCk = AprioriGenerate(l[k-2], k) # 产生k项候选集Ck# 计算候选k项集的支持度,找出满足最小支持度的候选集lk, supportk = scanData(data, Ck, min_support)support_data.update(supportk) # 添加支持度l.append(lk) #将k项的频繁集添加到l中k += 1del l[-1] # 注意l的最后一个值为空值,需要删除for i in l:# print(i[:])for j in i:# print(list(j)[:])frequentItem.append(list(j)[:])frequentItem = pd.DataFrame({"频繁项集": frequentItem})return l, support_data # 返回频繁项集和支持度,l是一个频繁项集列表
def obtainSubset(list1, list2):"""获取集合的所有子集"""for i in range(len(list1)):t = [list1[i]]t1 = frozenset(set(list1) - set(t)) # k-1项集if t1 not in list2:list2.append(t1)t1 = list(t1)if len(t1) > 1:obtainSubset(t1, list2) # 递归所有非1项子集
def CalculateConfidence(frequent, h, support_data, relation, min_confidence):"""计算置信度,找出满足最小置信度的数据:param frequent: k项频繁集:param h: k项频繁集对应的所有子集:param support_data: 支持度:param relation: 强关联规整:param min_confidence: 最小置信度"""global allresult# 遍历frequent中的所有子集并计算其置信度for i in h:con = support_data[frequent] / support_data[frequent - i]# 提升度lift = support_data[frequent] / (support_data[i] * support_data[frequent - i])if con >= min_confidence and lift > 1:print("{}-->{},支持度:{},置信度:{},lift值:{}".format(list(frequent - i)[:], list(i)[:], round(support_data[frequent], 6),round(con, 6), round(lift, 6)))allresult.loc[len(allresult)] = ["(" + " ".join(list(frequent - i)[:]).strip()+")"+"-->"+ "("+ " ".join(list(i)[:]).strip()+")",round(support_data[frequent], 6),round(con, 6),round(lift, 6)]# print("{}-->{},支持度:{},置信度:{},lift值:{}".format(frequent - i, i,# round(support_data[frequent], 6),# round(con, 6), round(lift, 6)))relation.append((frequent- i, i, con))
def AttainRelation(l, support_data, min_confidence = 0.65):"""生成强关联规则:param l: 频繁集:param support_data: 支持度:param min_confidence: 最小置信度:return: 强关联规则"""rela = [] # 存放强关联规整# 从2项频繁集开始计算置信度for i in range(1, len(l)):for j in l[i]:h = list(j)sonlist = [] # 存放h的所有子集# 生成所有子集obtainSubset(h, sonlist)# print(sonlist)# 计算置信度,找出满足最小置信度的数据CalculateConfidence(j, sonlist, support_data, rela, min_confidence)return rela # 强相关规整
if __name__ == "__main__":data = DealData()global frequentItem # 定义全局变量,用于存储频繁项集frequentItem = []global allresult # 定义全局变量,用于存储强关联allresult = pd.DataFrame(columns=["rule", "support", "confidence", "lift"])# 返回频繁集及其对应的支持度L, supportData = Apriori(data, min_support=0.02)# 生成强关联规则rule = AttainRelation(L, supportData, min_confidence=0.30)# 按照置信度降序排序allresult.sort_values(by="confidence",ascending=False, inplace=True)print(frequentItem)print(allresult.reset_index(drop=True))由于前面以经使用python封装好的第三方库调用了Apriori算法进行计算,所以这里就直接使用前面已经得出的结果,将最小支持度设定为0.02,最小置信度设定为0.3,得到122个频繁项集,37条关联规则,如下图所示。


销售策略
针对以上计算的结果,我发现(其他蔬菜,酸奶)全脂牛奶这一条的关联规则是置信度最高的。

置信度为0.51。但是它们之间并不是十分明显的强关联,而且酸奶和全脂牛奶在人们的日常生活中是可以互相替代的商品,根据市场产品销售波动理论,互相替代的产品彼此之间有着明显的竞争关系,是很难出现一荣俱荣,一损俱损的。因此在日常销售中,应该将全脂牛奶和酸奶放在一起销售,减小空间上的距离有助于顾客消费这两种商品,如果这两种商品距离过远,很多顾客出于少走两步买不必要商品的心理就会减少购物欲望。
(面包卷)—>(全脂牛奶)是支持度最高的关联规则

其支持度为0.05634,这个值是比较低的,因此也要将面包卷放在全脂牛奶的附近,有利于销量的增加。
根据前面的数据分析阶段,我大致推测该店铺靠近居民区,主要为社区居民提供日常餐饮类商品,通过前面的计算,并没有发现很明显的强关联规则,因此很多彼此有联系的商品对于消费者来说都是可买可不买的,如果能够在消费者购物的时候增加这些可买可不买的商品曝光度,那么就会大大增加顾客购买消费的概率,从而提高店铺的销售收入,尤其是销量前三的商品,全脂牛奶、其他蔬菜、面包卷,通过前面的计算,我发现酸奶、黄油、凝乳、根茎类蔬菜、本地蛋类、冷冻蔬菜、人造黄油、热带水果、仁果类水果、黑面包、猪肉、柑橘类水果、香肠等商品都和销量前三的商品有关联。将这些与销量前三有关系的商品放在一起,或者放在顾客的必经之路上,将会大大增加这些商品的销量。
四、实验代码
数据分析代码
'''
python3.7
-*- coding: UTF-8 -*-
@Project -> File :Code -> d1
@IDE :PyCharm
@Author :YangShouWei
@USER: 296714435
@Date :2021/4/19 14:47:16
@LastEditor:
'''import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt# 加载数据
order_data = pd.read_csv("GoodsOrder.csv")
types_data = pd.read_csv("GoodsTypes.csv")# 原始数据集缺失值情况。
print("GoodsOrder数据的缺失值情况:\n",order_data.isnull().sum())
print("GoodsTypes数据的缺失情况:\n",types_data.isnull().sum())# 数据形状
print("GoodsOrder表形状:",order_data.shape)
print("GoodsTypes表形状:",types_data.shape)# 将两张表中的数据进行连接
outer = pd.merge(order_data, types_data, on='Goods', how='outer')
print("两个原始数据表外连接后的形状:\n",outer.shape)
print(outer)
inner = pd.merge(order_data, types_data, on='Goods')
print("两个原始数据表内连接后的形状:\n",inner.shape)
print(inner)# 重新设置order数据索引
data1 = order_data.reset_index()
print("order数据集的重复值情况",data1.duplicated().sum())# 对购物篮数据进行描述性分析
print("描述性分析:\n",data1.describe())# 统计销量前10的商品
# 按照Goods列进行分组然后计数,并重新设置索引。
group = data1.groupby(['Goods']).count().reset_index()
# print("group:\n",group)
# 按照id进行降序排列
sort = group.sort_values(by='id',ascending = False).reset_index(drop=True)
# print("sort:\n",sort)plt.rcParams['font.sans-serif'] = ['SimHei'] # 设置图形里面中文为黑体
# 绘制销量前10的商品数理统计图
plt.figure(figsize=(8, 5))
sns.barplot(x=sort.iloc[:10,0],y=sort.iloc[:10,1])
plt.ylabel('商品销量',fontsize=15)
plt.xlabel('商品类别',fontsize=15)
plt.title('销量排名前10的商品销量情况',fontsize=20)# 销量前十的商品销售情况
print("商品名称\t商品销量\t商品销量占所有商品总销量的比例")
part = []
for index, i in sort[:10].iterrows():print("{}\t{}\t{}".format(i['Goods'],i["id"], i["id"]/len(data1)))part.append(i["id"]/len(data1))# 销量前十的商品销量占比统计图
plt.figure(figsize=(8, 5))
plt.plot(sort.iloc[:10, 0], part)
plt.title("销量前十的商品占比折线图", fontsize=20)
plt.xlabel("商品类别", fontsize=14)
plt.ylabel("比率", fontsize=14)# 绘制销量最后10位的商品数量统计图
plt.figure(figsize=(8,5))
# plt.plot(sort.iloc[-10:, 0],sort.iloc[-10:, 1]) # 绘制折线图
sns.barplot(x=sort.iloc[-10:, 1],y=sort.iloc[-10:, 0])
plt.xlabel("商品销量")
plt.ylabel("商品类别")
plt.title("销量排名最后10位的商品销量情况",fontsize=20)# 销量最后十位的商品销售情况
print("商品名称\t商品销量\t商品销量占所有商品总销量的比例")
part = []
for index, i in sort[-10:].iterrows():print("{}\t{}\t{}".format(i['Goods'],i["id"], i["id"]/len(data1)))part.append(i["id"]/len(data1))# 绘制销量最后10位的商品销量占比统计图
plt.figure(figsize=(8, 5))
plt.plot(sort.iloc[-10:, 0], part)
plt.title("销量最后十位的商品占比折线图", fontsize=20)
plt.xlabel("商品类别", fontsize=14)
plt.ylabel("比率", fontsize=14)# 统计每个商品类别的销量及占比
type_count = outer.groupby("Types").count().reset_index()
type_count["rate"] = type_count["Goods"]/len(data1) # 计算商品类别销量占比
type_count.sort_values("id",ascending=False,inplace=True) # 对销量进行降序排序
print(type_count.reset_index(drop=True))# 绘制每个商品类别的销量占比饼状图
plt.figure(figsize=(6,5))
plt.pie(x=type_count["rate"],labels=type_count["Types"],autopct='%1.2f%%',labeldistance=1.05)
plt.axis('equal') # 显示为圆(避免比例压缩为椭圆)
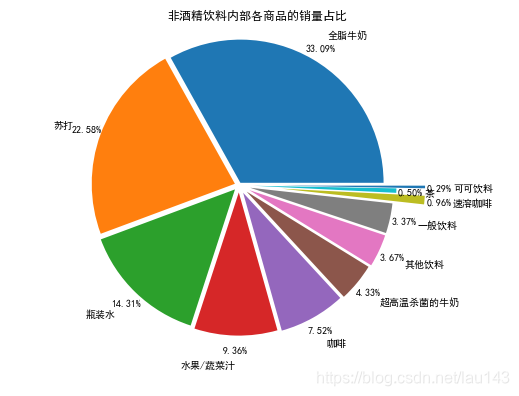
plt.title('不同商品类型销量占比',fontsize=15)# 非酒精饮料的商品销量统计
drink = outer[outer["Types"] == "非酒精饮料"].groupby("Goods").count().reset_index()
# print(drink)
# print(list(drink["id"]))
# print(list(drink["Goods"]))# 绘制非酒精饮料类别中不同商品占比的饼状图
# plt.figure(figsize=(6,5))
# plt.pie(x=list(drink["id"]),labels=list(drink["Goods"]),autopct='%1.2f%%',labeldistance=1.05)
# plt.axis('equal') # 显示为圆(避免比例压缩为椭圆)
# plt.title('非酒精饮料类别中不同商品销量占比',fontsize=15)# 绘制非酒精饮料类别中不同商品占比的条形图
plt.figure(figsize=(10, 5))
sns.barplot(x=list(drink["id"]), y=list(drink["Goods"]))
plt.title("非酒精饮料类别中不同商品的销量", fontsize= 15)
plt.xlabel("商品销量")
plt.ylabel("商品类别")# 西点
pastry = outer[outer["Types"] == "西点"].groupby("Goods").count().reset_index()
# 绘制西点类别中不同商品占比的条形图
plt.figure(figsize=(10, 5))
sns.barplot(x=list(pastry["id"]), y=list(pastry["Goods"]))
plt.title("西点类别中不同商品的销量", fontsize= 15)
plt.xlabel("商品销量")
plt.ylabel("商品类别")# 果蔬
pastry = outer[outer["Types"] == "果蔬"].groupby("Goods").count().reset_index()
# 绘制果蔬类别中不同商品占比的条形图
plt.figure(figsize=(10, 5))
sns.barplot(x=list(pastry["id"]), y=list(pastry["Goods"]))
plt.title("果蔬类别中不同商品的销量", fontsize= 15)
plt.xlabel("商品销量")
plt.ylabel("商品类别")plt.show()# 将同一张订单里面的商品合并
# 遍历订单数据中的每一行,在每个商品名后面添加一个空格,便于将同一张订单里面的商品合并到一起。
order_data["Goods"] = order_data["Goods"].map(lambda x : x+" ")
order_data = order_data.groupby("id").sum().reset_index() # 按照订单号进行分组,然后进行同一张订单的商品合并。order = [] # 存放每一张订单中的商品,二维矩阵
for index, i in order_data.iterrows():t = i["Goods"].split(" ") # 将订单中的商品分割成每一个商品t.pop(-1) # 删除空格元素order.append(t)
# print(order)调用Python封装好的Apriori算法库
'''
python3.7
-*- coding: UTF-8 -*-
@Project -> File :Code -> Apriori
@IDE :PyCharm
@Author :YangShouWei
@USER: 296714435
@Date :2021/4/20 13:47:49
@LastEditor:
'''
import pandas as pd
import numpy as np
from mlxtend.frequent_patterns import apriori # 生成频繁项集
from mlxtend.frequent_patterns import association_rules # 生成强关联规则
import warnings # 消除警告warnings.filterwarnings("ignore") # 排除程序运行时的警告def DealData(): # 数据预处理Order_data = pd.read_csv("GoodsOrder.csv")# 遍历每一个商品名,在其后面加上一个空格,便于合并每一张订单中的所有商品Order_data["Goods"] = Order_data["Goods"].map(lambda x : x+" ")Order_data = Order_data.groupby("id").sum().reset_index()# print(Order_data)# 将每一张订单中的每一个商品提取出来Order_data["Goods"] = Order_data["Goods"].map(lambda x:x.strip().split(" "))order = list(Order_data["Goods"])# print(order)return orderif __name__ =="__main__":order = DealData()column_list = []for var in order:column_list = set(column_list) | set(var)# print(column_list)print('将订单数据转换成0-1矩阵')# 建立一个data = pd.DataFrame(np.zeros((len(order), 169)), columns=column_list)# print(data.index)for i in range(len(order)):for j in order[i]:# print(i, j)data.loc[i, j] += 1# print(data)# Apriori算法output = apriori(data, min_support=0.02, use_colnames=True)output = pd.DataFrame(output) # 将结果转换成DataFrame形式# 按照支持度进行降序排序output.sort_values(by="support", ascending=False, inplace=True)# print(output.head(20))print(output.reset_index(drop=True))# 将结果保存至CSV文件output.to_csv("frequent.csv", index=False, encoding="gbk")# 生成关联准则relation = association_rules(output, metric="confidence", min_threshold=0.3)relation = pd.DataFrame(relation)# 按照置信度的大小进行降序排序relation.sort_values(by="confidence", ascending=False, inplace=True)# pd.set_option('display.max_columns', 5) # 设置最大显示列数的多少# print(relation)print(relation.iloc[:,:6])# 将结果保存至CSV文件relation.to_csv("relation.csv", index = False, encoding="gbk")手动实现Apriori算法
'''
python3.7
-*- coding: UTF-8 -*-
@Project -> File :Code -> hand
@IDE :PyCharm
@Author :YangShouWei
@USER: 296714435
@Date :2021/4/20 19:14:02
@LastEditor:
'''
import pandas as pddef DealData(): # 数据预处理Order_data = pd.read_csv("GoodsOrder.csv")# 遍历每一个商品名,在其后面加上一个空格,便于合并每一张订单中的所有商品Order_data["Goods"] = Order_data["Goods"].map(lambda x : x+" ")Order_data = Order_data.groupby("id").sum().reset_index()# print(Order_data)# 将每一张订单中的每一个商品提取出来Order_data["Goods"] = Order_data["Goods"].map(lambda x:x.strip().split(" "))order = list(Order_data["Goods"])# print(order)return orderdef findOneSet(data):"""计算1项候选集C1:param data: 数据集:return: 1项候选集"""C1 = []for i in data: # i为每一行的数据for j in i: # j为每一列的数据,即一张订单中的单个商品元素if [j] not in C1:C1.append([j])C1 = list(map(frozenset, C1)) # 将集合C1冻结,不能添加或者删除元素。return C1def CalculateSupport(data, C, min_support):"""计算1项候选集的支持度,剔除不满足最小支持度的项集:param data::param C::param min_support: 最小支持度:return: 频繁1项集及其支持度"""dict_c = dict() # 存储中间值,用于计数# 统计项集中的每一项元素for i in data:for j in C:if j.issubset(i): # 判断j是否为i的子集if j not in dict_c: # 判断是否统计过该元素dict_c[j] = 1 # 没有统计过就初始化为1else:dict_c[j] += 1sumc = float(len(data)) # 事务的总数# 计算支持度sd = dict() # 用于存放频繁集的支持度listc = [] # 存放频繁项集for i in dict_c:t = dict_c[i] /sumc # 计算支持度,临时存放# 存下满足最小支持度的频繁项集if t > min_support:listc.append(i) # 添加评频繁1项集sd[i] = t # 存入支持度return listc, sd # 返回频繁一项集和支持度def AprioriGenerate(lk, k):"""利用剪枝算法,找出k项候选集:param lk: 频繁k-1项集:param k: 第k项:return: 第k项候选集"""listk = [] # 存放第k项候选集length_lk = len(lk) # 第k-1项频繁集的长度# 两两组合for i in range(length_lk):for j in range(i+1, length_lk):l1 = list(lk[i])[:k-2]l2 = list(lk[j])[:k-2]l1.sort()l2.sort()#前k-1项相等,就可以相乘,从而防止重复项出现if l1 == l2:s = lk[i] | lk[j] # s是被冻结的集合,不能增加删除元素# 进行剪枝s1 = list(s)son = [] # 她的所有k-1项子集# 构造son,遍历每一个商品元素,转换成集合set,依次从s1中删除该元素,并加入到son中for x in range(len(s1)):t = [s1[x]]t1 = frozenset(set(s1)- set(t))son.append(t1)# 当son都是频繁项集时,保留s1c = 0for r in son:if r in lk: # 判断是否属于候选集c += 1# 所有子集都是候选集则其自身为候选集if len(son) == c:listk.append(son[0] | son[1])return listkdef scanData(data, Ck, min_support):"""计算候选k项集的支持度,找出满足最小支持度的频繁k项集及其支持度:param data: 数据集:param Ck: 候选k项集:param min_support 最小支持度::return: 返回频繁k项集"""dicts = dict() # 存放支持度for i in data:for j in Ck:if j.issubset(i):if j not in dicts:dicts[j] = 1else:dicts[j] += 1# 计算支持度sumi = len(data) # 事务总数listck = [] # 存放频繁k项集sd = dict() # 存放频繁集的支持度for q in dicts:s = dicts[q] / sumiif s > min_support: # 判段支持度是否满足最小支持度listck.insert(0, q)sd[q] = s# 返回频繁k项集和其支持度return listck, sddef Apriori(data, min_support=0.1):"""Apriori关联规整算法:param data: 数据集:param min_support: 最小支持度:return: 频繁项集和支持度"""global frequentItem# 先找到1项候选集C1 = findOneSet(data)# 将数据转换成列表,方便计算支持度data = list(map(set,data))# 计算1项候选集的支持度,找到满足最小支持度的项集l1, support_data = CalculateSupport(data, C1, min_support)l = [l1] #添加到列表之中,使得1项频繁集成一个单独的元素k = 2 # k项while len(l[k-2]) > 0: # 循环直到没有候选集结束# 产生k项候选集CkCk = AprioriGenerate(l[k-2], k) # 产生k项候选集Ck# 计算候选k项集的支持度,找出满足最小支持度的候选集lk, supportk = scanData(data, Ck, min_support)support_data.update(supportk) # 添加支持度l.append(lk) #将k项的频繁集添加到l中k += 1del l[-1] # 注意l的最后一个值为空值,需要删除for i in l:# print(i[:])for j in i:# print(list(j)[:])frequentItem.append(list(j)[:])frequentItem = pd.DataFrame({"频繁项集": frequentItem})return l, support_data # 返回频繁项集和支持度,l是一个频繁项集列表def obtainSubset(list1, list2):"""获取集合的所有子集"""for i in range(len(list1)):t = [list1[i]]t1 = frozenset(set(list1) - set(t)) # k-1项集if t1 not in list2:list2.append(t1)t1 = list(t1)if len(t1) > 1:obtainSubset(t1, list2) # 递归所有非1项子集def CalculateConfidence(frequent, h, support_data, relation, min_confidence):"""计算置信度,找出满足最小置信度的数据:param frequent: k项频繁集:param h: k项频繁集对应的所有子集:param support_data: 支持度:param relation: 强关联规整:param min_confidence: 最小置信度"""global allresult# 遍历frequent中的所有子集并计算其置信度for i in h:con = support_data[frequent] / support_data[frequent - i]# 提升度lift = support_data[frequent] / (support_data[i] * support_data[frequent - i])if con >= min_confidence and lift > 1:# print("{}-->{},支持度:{},置信度:{},lift值:{}".format(list(frequent - i)[:], list(i)[:], round(support_data[frequent], 6),# round(con, 6), round(lift, 6)))allresult.loc[len(allresult)] = ["(" + " ".join(list(frequent - i)[:]).strip()+")"+"-->"+ "("+ " ".join(list(i)[:]).strip()+")",round(support_data[frequent], 6),round(con, 6),round(lift, 6)]# print("{}-->{},支持度:{},置信度:{},lift值:{}".format(frequent - i, i,# round(support_data[frequent], 6),# round(con, 6), round(lift, 6)))relation.append((frequent- i, i, con))def AttainRelation(l, support_data, min_confidence = 0.65):"""生成强关联规则:param l: 频繁集:param support_data: 支持度:param min_confidence: 最小置信度:return: 强关联规则"""rela = [] # 存放强关联规整# 从2项频繁集开始计算置信度for i in range(1, len(l)):for j in l[i]:h = list(j)sonlist = [] # 存放h的所有子集# 生成所有子集obtainSubset(h, sonlist)# print(sonlist)# 计算置信度,找出满足最小置信度的数据CalculateConfidence(j, sonlist, support_data, rela, min_confidence)return rela # 强相关规整if __name__ == "__main__":data = DealData()global frequentItem # 定义全局变量,用于存储频繁项集frequentItem = []global allresult # 定义全局变量,用于存储强关联allresult = pd.DataFrame(columns=["rule", "support", "confidence", "lift"])# 返回频繁集及其对应的支持度L, supportData = Apriori(data, min_support=0.02)# 生成强关联规则rule = AttainRelation(L, supportData, min_confidence=0.30)# 按照置信度降序排序allresult.sort_values(by="confidence",ascending=False, inplace=True)print(frequentItem)print(allresult.reset_index(drop=True))实验总结
这次实验是我第一次接触关联挖掘Apriori的底层算法,虽然之前也看过关联挖掘Apriori算法,但是并没有进行深入的研究。虽然上课老师讲解了Apriori算法并且书上也给出了伪代码的示例,但是真的去自己手敲一遍底层算法难度还是挺大的,研究了课本的伪代码,也在网上找了很多参考资料才磕磕绊绊勉强把Apriori算法手动实现。
虽然这个过程难度挺大的,但是我也花了很多时间去钻研,学到了很多新的知识,对于关联挖掘有了深入的了解和认识,真的受益匪浅。
参考文献:数据挖掘实战—商品零售购物篮分析

![[Python] 电商平台用户的购物篮分析](https://img-blog.csdnimg.cn/20201001091330238.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2xhbV95eA==,size_16,color_FFFFFF,t_70#pic_center)








![[windows]修改本机host配置](https://img-blog.csdnimg.cn/20200929161406301.gif#pic_center)