数据挖掘实战—商品零售购物篮分析

文章目录

- 引言
- 一、数据探索性分析
- - 1.数据质量分析
  - - 1.1 缺失值分析
    - 1.2 异常值分析
    - 1.3 重复数据分析
  - 2.数据特征分析
  - - 2.1 描述性统计分析
    - 2.2 分布分析
    - - 2.2.1 商品热销情况分布分析
      - 2.2.2 按类别划分商品销量分布分析
      - 2.2.3 商品内部结构分布分析
- 二、数据预处理
- 三、模型构建

案例数据百度网盘链接-提取码：1234
使用的notebook百度网盘链接-提取码：1234

传送门：

数据挖掘实战—财政收入影响因素分析及预测
数据挖掘实战—航空公司客户价值分析
数据挖掘实战—商品零售购物篮分析
数据挖掘实战—基于水色图像的水质评价
数据挖掘实战—家用热水器用户行为分析与事件识别
数据挖掘实战—电商产品评论数据情感分析

引言

购物篮分析是通过发现顾客在一次购买行为中放入购物篮中不同商品之间的关联，研究顾客的购买行为，从而辅助零售企业制定营销策略的一种数据分析方法。本文使用Apriori关联规则算法实现购物篮分析，发现超市不同商品之间的关联关系，并根据商品之间的关联规则制定销售策略。定义数据挖掘目标如下：

构建零售商品的Apriori关联规则模型，分析商品之间的关联性
根据模型结果给出销售策略

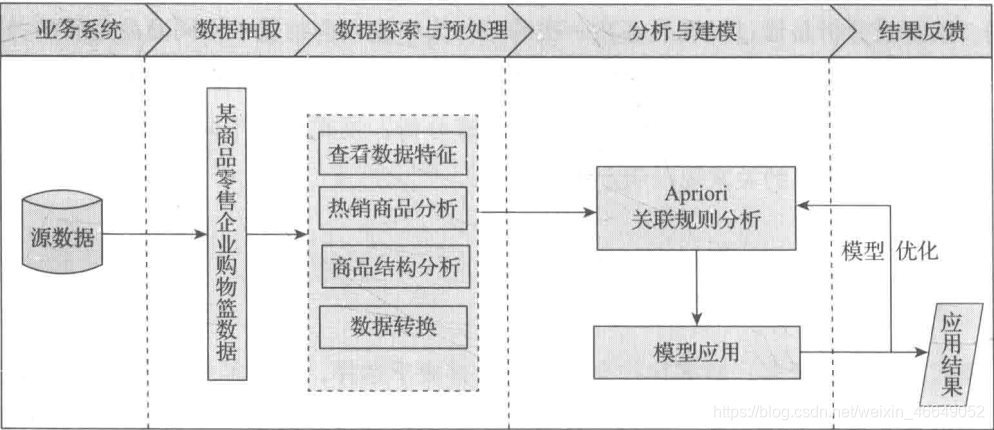
购物篮关联规则分析数据挖掘步骤如下：

对原始数据进行探索性分析，分析商品的热销情况与商品结构
对原始数据进行数据预处理，转换数据形式，使之符合Apriori关联规则算法要求
采用Apriori关联规则算法调整模型的输入参数，完成商品的关联性分析
结合实际业务，对模型结果进行分析，给出对应的销售策略

在这里插入图片描述

一、数据探索性分析

%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import missingno as mg# 加载数据
order_data = pd.read_csv('data/GoodsOrder.csv',index_col=0,header=0,encoding='gbk')
type_data = pd.read_csv('data/GoodsTypes.csv',index_col=0,header=0,encoding='gbk')

1.数据质量分析

1.1 缺失值分析

order_data.isnull().sum()

在这里插入图片描述
数据中不含有缺失值

1.2 异常值分析

a = 0
b = 0
for i in order_data['Goods']:if i in list(type_data.index):a += 1else:b += 1
print(a,b)
# 43285 82

发现第一表中的部分商品名称没有在第二个表格中出现，可能存在异常值

1.3 重复数据分析

data = order_data.reset_index() #重置索引
data.duplicated().sum()

在这里插入图片描述
发现数据中没有重复值

2.数据特征分析

2.1 描述性统计分析

data.describe().T

在这里插入图片描述
发现共有43367个观测值（售出商品总数），不存在缺失值，共有9835条购物篮数据

2.2 分布分析

2.2.1 商品热销情况分布分析

通过对Goods列进行统计，可以进行商品热销情况分析，计算销量排行前10的商品销量。有以下两种方式：

group = data.groupby(['Goods']).count().reset_index() # 计数
sort = group.sort_values(by='id',ascending = False).reset_index(drop=True)

在这里插入图片描述

order_data.Goods.value_counts().reset_index()

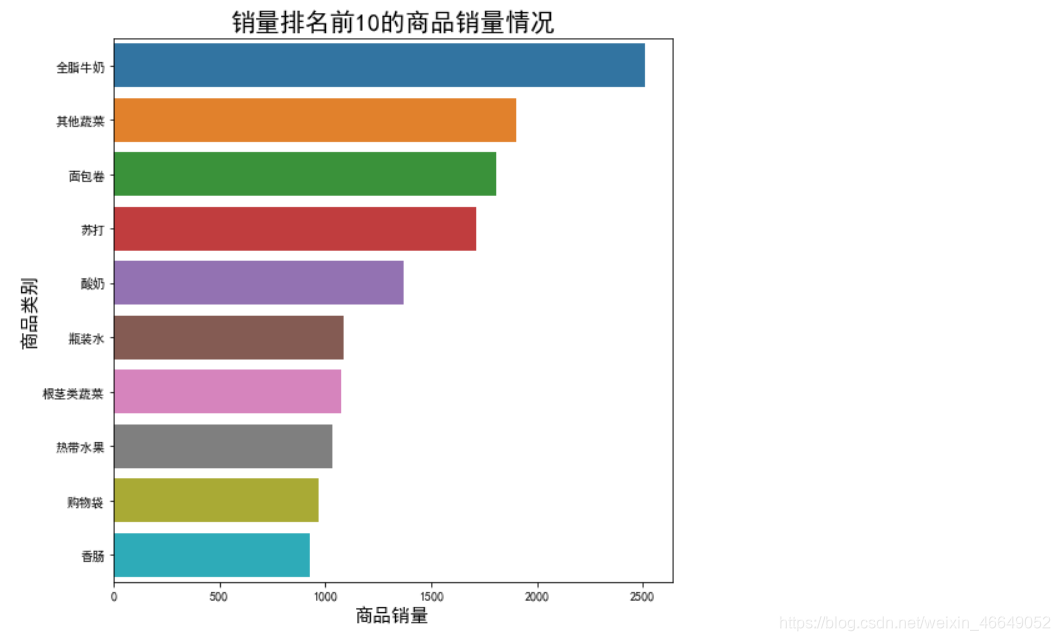
在这里插入图片描述

print('销量排行前10的商品销量\n',sort[:10])

在这里插入图片描述

fig,ax = plt.subplots(figsize=(8,8))
# ax.barh(sort.iloc[:10,0],sort.iloc[:10,1])
sns.barplot(y=sort.iloc[:10,0],x=sort.iloc[:10,1])
ax.set_xlabel('商品销量',fontsize=15)
ax.set_ylabel('商品类别',fontsize=15)
ax.set_title('销量排名前10的商品销量情况',fontsize=20)
plt.savefig('Top10.png')

在这里插入图片描述

# 计算销量前10的商品占比
for index,row in sort[:10].iterrows():print(row['Goods'],row['id'],row['id']/len(data))

在这里插入图片描述
通过以上分析，我们得出商品销量前10的商品以及它们的销量占比

2.2.2 按类别划分商品销量分布分析

接下来，将商品归类，分析各类商品的销量及占比情况

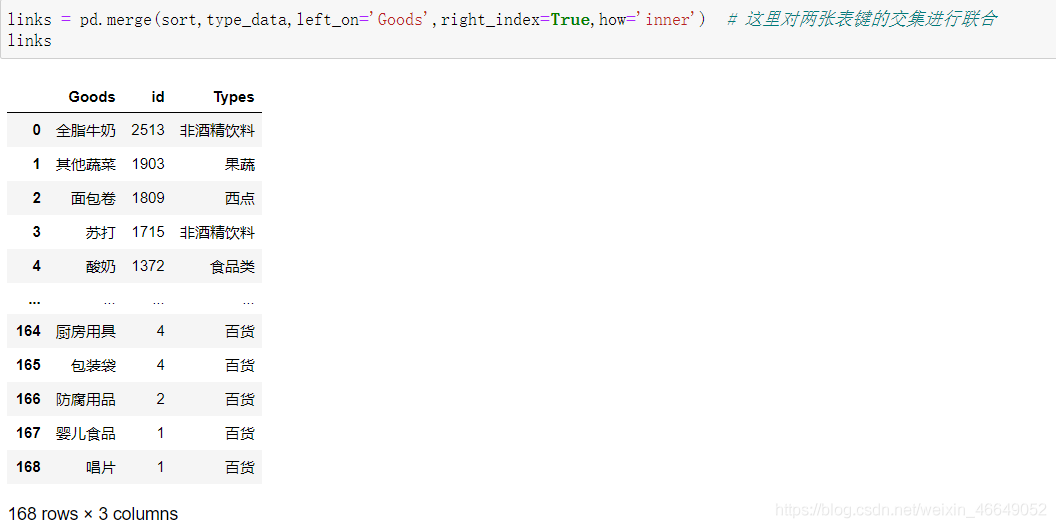
links = pd.merge(sort,type_data,left_on='Goods',right_index=True,how='inner')  # 这里对两张表键的交集进行联合

这里对两个表中键的交集进行联合，消除了异常值。
在这里插入图片描述

求每个类别商品的销量

# 根据商品类别进行分组并求和
type_links = links.groupby(['Types']).sum().reset_index()
# 排序
type_links = type_links.sort_values('id',ascending=False).reset_index(drop=True)

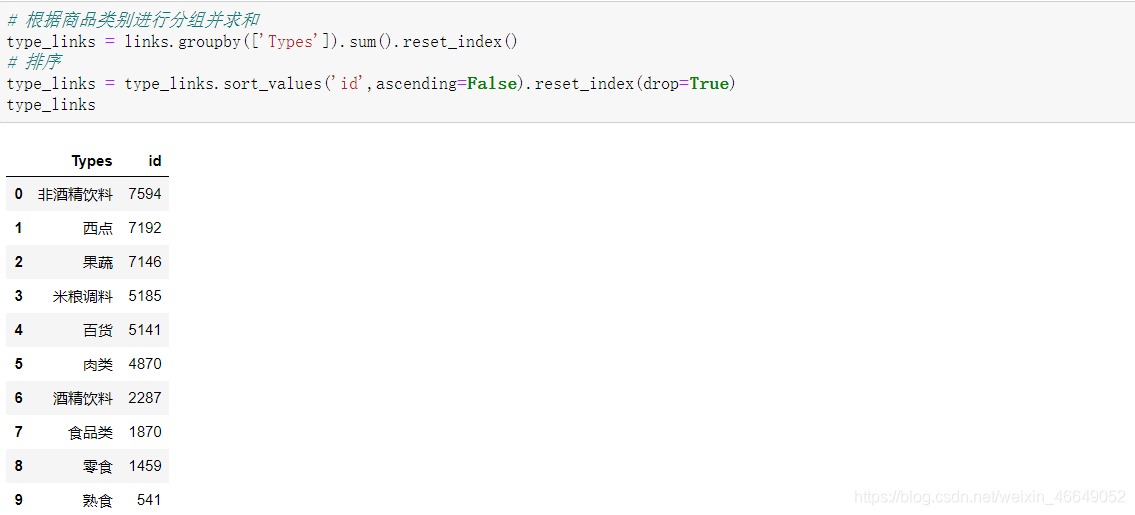
在这里插入图片描述
求每个类别商品的销量占比

# axis = 0对每一列应用函数，axis=1对每行应用函数
type_links['count'] = type_links.apply(lambda x : x['id'] / len(order_data),axis=1)
# 重命名
type_links.rename(columns={'count':'percent'},inplace=True)
print('各类商品的销量及占比\n',type_links)
type_links.to_csv('percent.csv',index=False,header=True,encoding='gbk')

在这里插入图片描述
绘制各类别销量占比的饼状图

# 画饼图展示每类商品的销量占比
data = type_links['percent']
label = type_links['Types']
plt.figure(figsize=(8,8))
plt.pie(data,labels=label,autopct='%1.2f%%',labeldistance=1.05,shadow=True)
plt.axis('equal')  # 显示为圆（避免比例压缩为椭圆）
plt.title('每类商品销量占比',fontsize=20)
plt.savefig('percent.png')

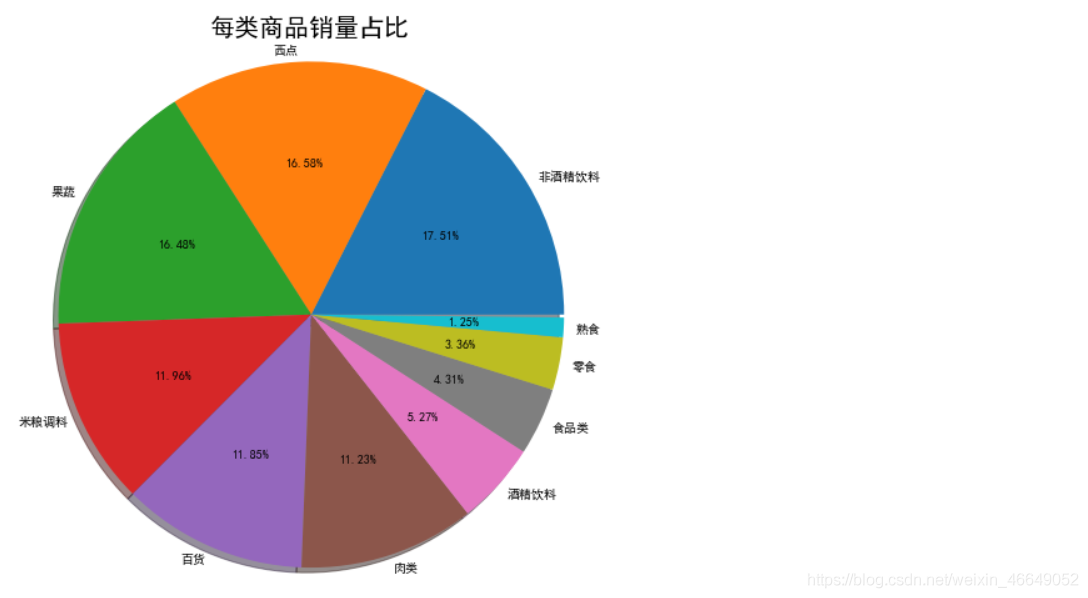
在这里插入图片描述
从饼状图中可以看出：果蔬、西点、非酒精饮料这3类商品的销量差距不大，占总销量的50%左右。同时。按大类划分，食品类销量总和接近90%左右，说明顾客倾向于购买食品类商品，其他商品并非销售主力。

2.2.3 商品内部结构分布分析

通过饼状图，我们可以发现非酒精饮料销量第1，我们以非酒精饮料为例，展示非酒精饮料的商品结构。我们先在links筛选出非酒精饮料的商品名称，然后在统计每一个商品名称的销量及占比

selected = links.loc[links.Types == '非酒精饮料']

在这里插入图片描述
计算每一种非酒精饮料的占比

noalcohol = selected['id'].sum()
selected['count'] = selected.apply(lambda x : x['id']/noalcohol,axis=1)
selected.rename(columns={'count':'percent'},inplace=True)

在这里插入图片描述
饼状图展示非酒精饮料的商品结构

# 画饼状图
data = selected['percent']
label = selected['Goods']
plt.figure(figsize=(8,8))
plt.pie(data,labels=label,autopct='%1.2f%%',labeldistance=1.05)
plt.axis('equal')  # 显示为圆（避免比例压缩为椭圆）
plt.title('非酒类饮料的商品结构',fontsize=20)
plt.savefig('noalcohol.png')

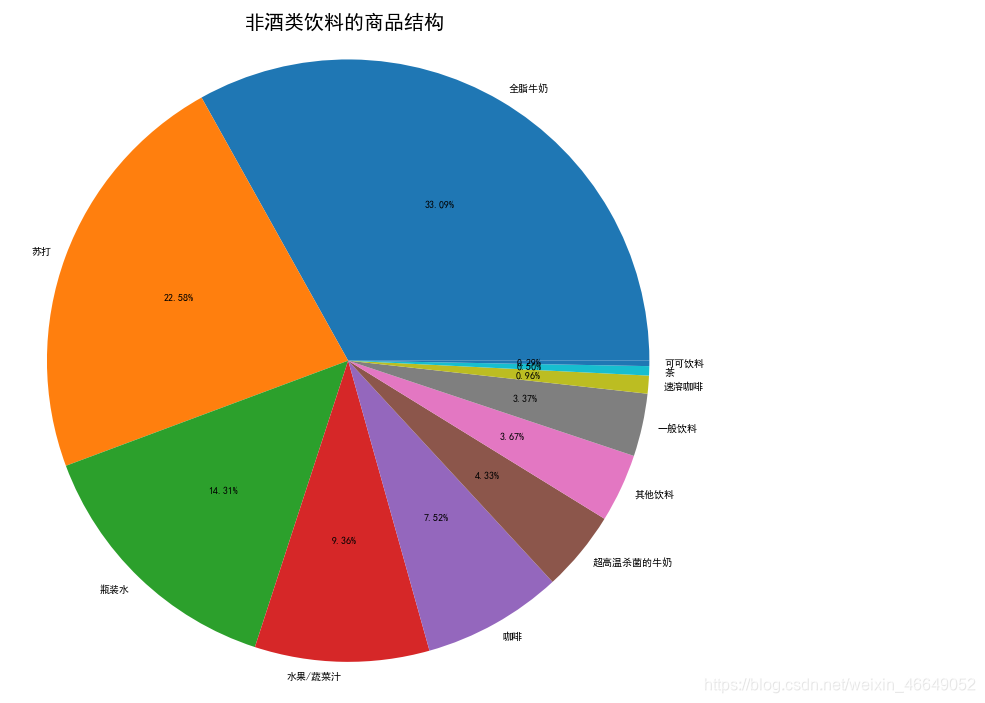
在这里插入图片描述
同理，我们可以得到其他类别商品的商品结构
西点：

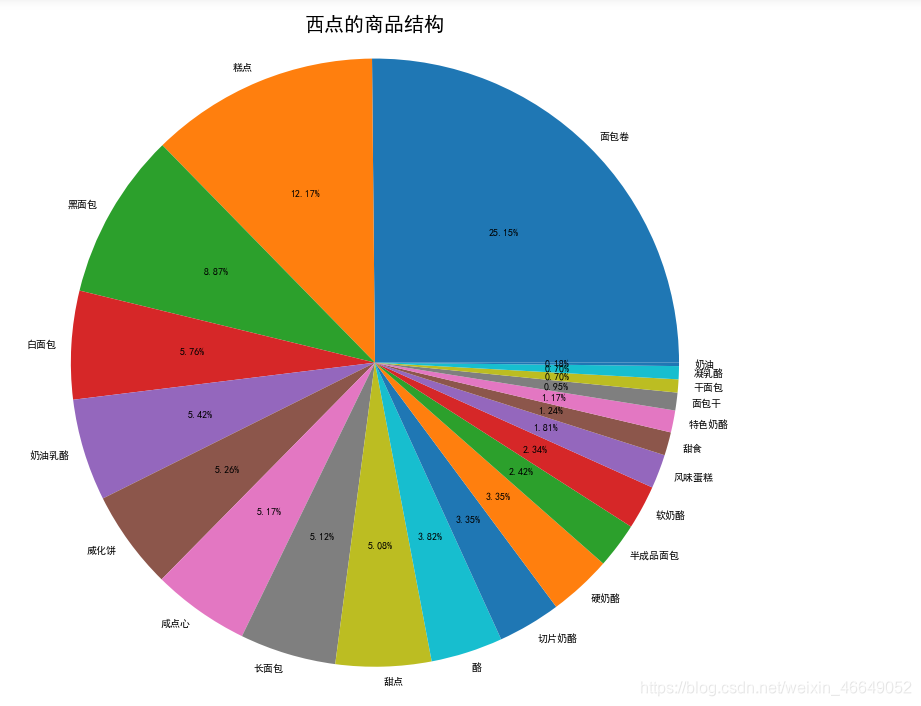
果蔬：
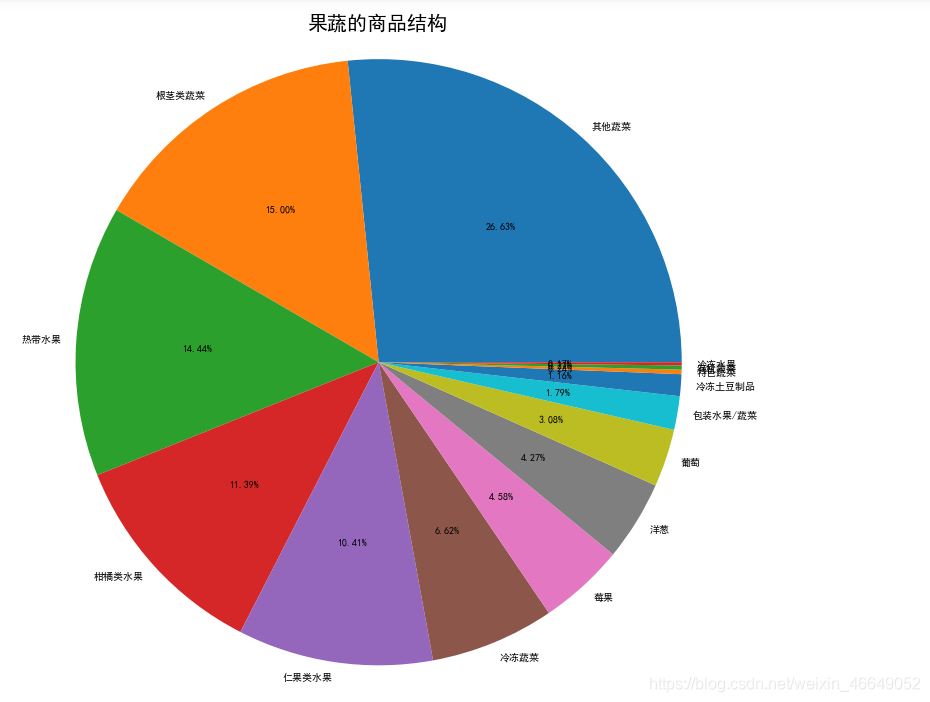
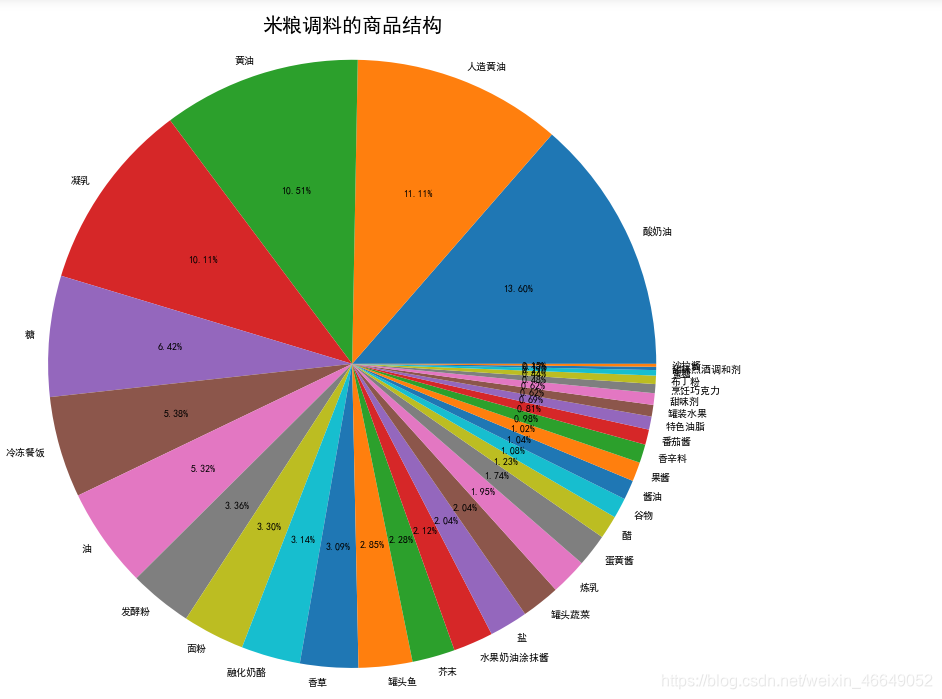
在这里插入图片描述
米粮调料：

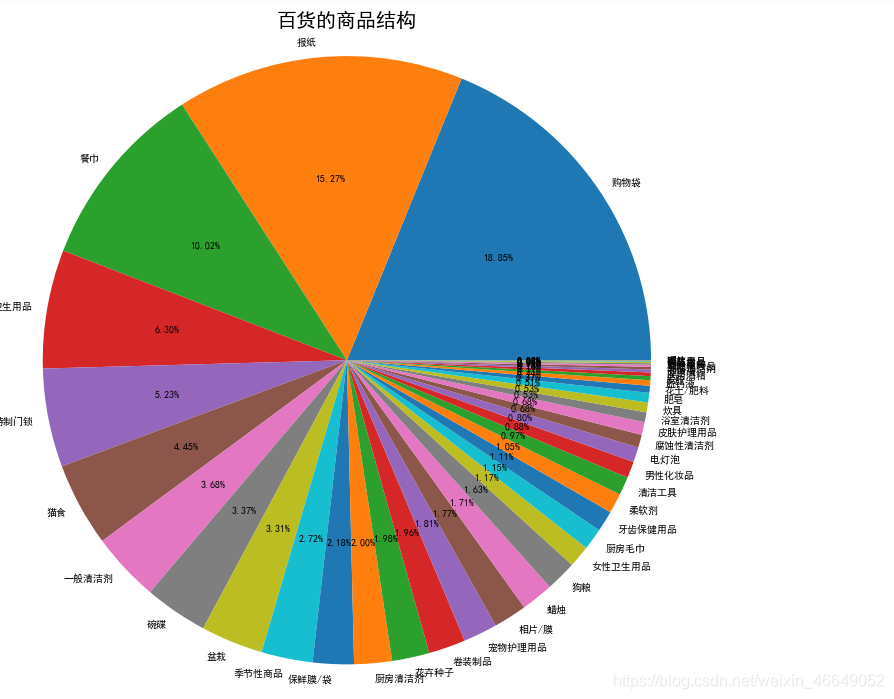
百货：

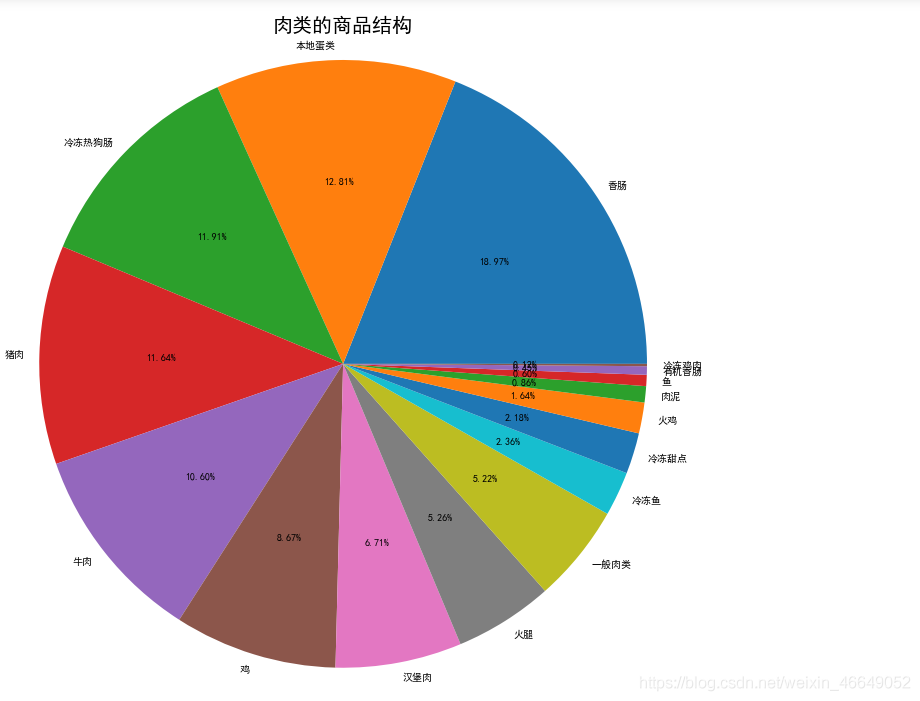
肉类：

酒精饮料：

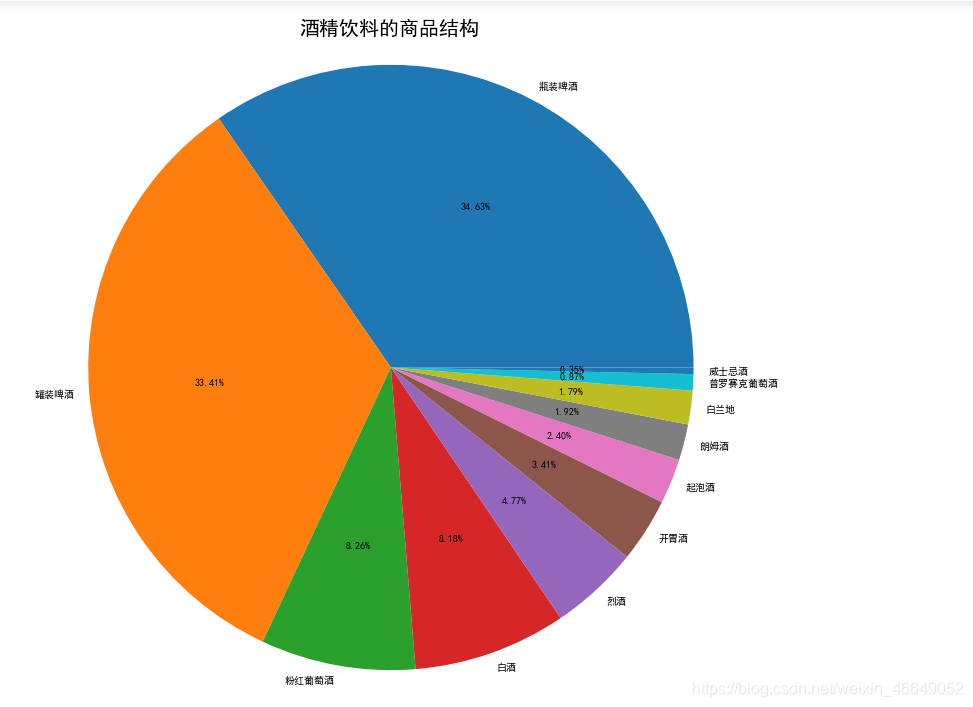
食品类：

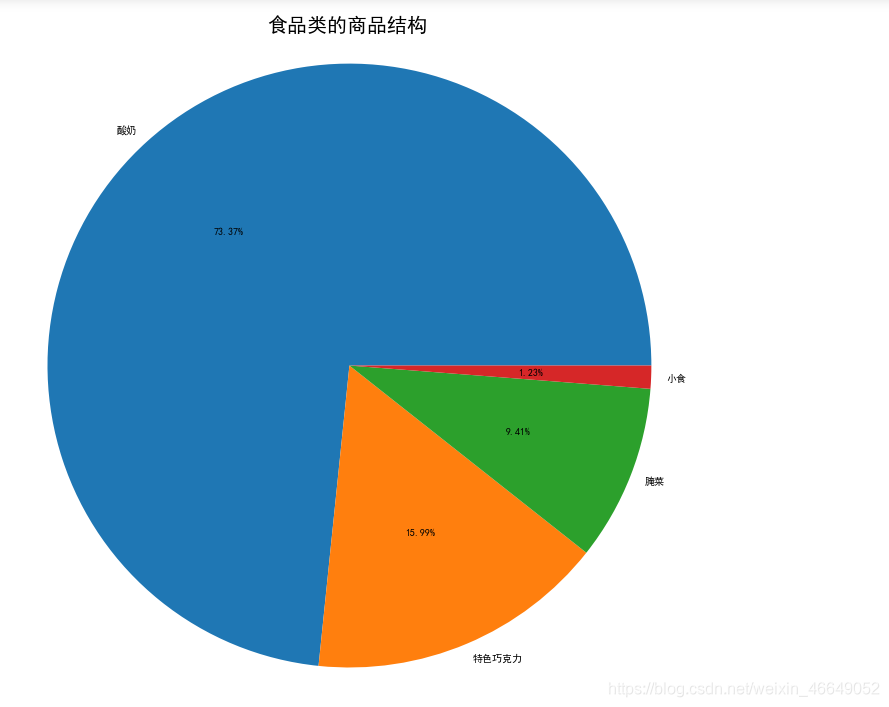
零食：

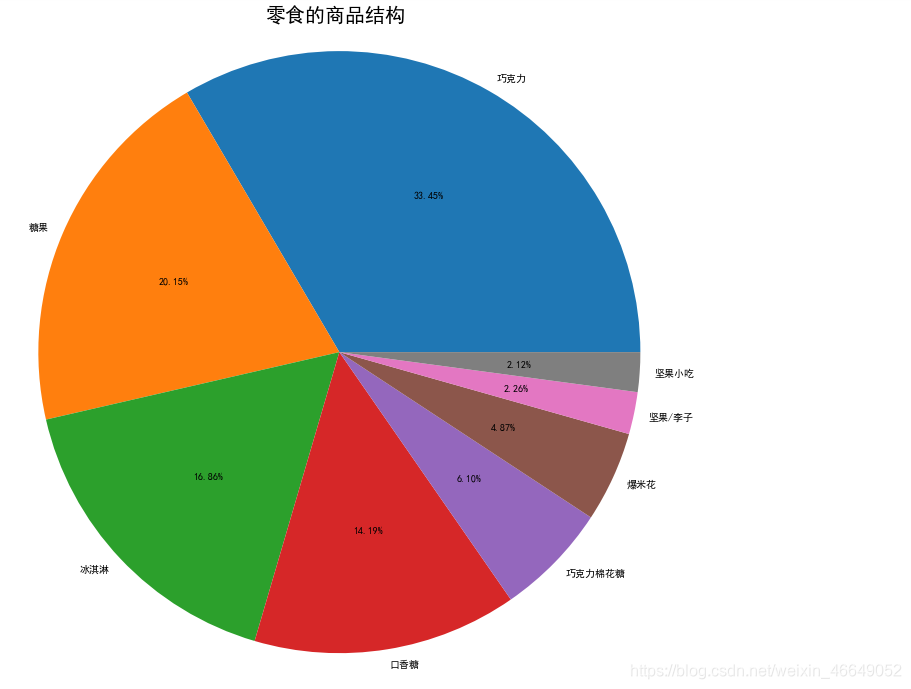
熟食：

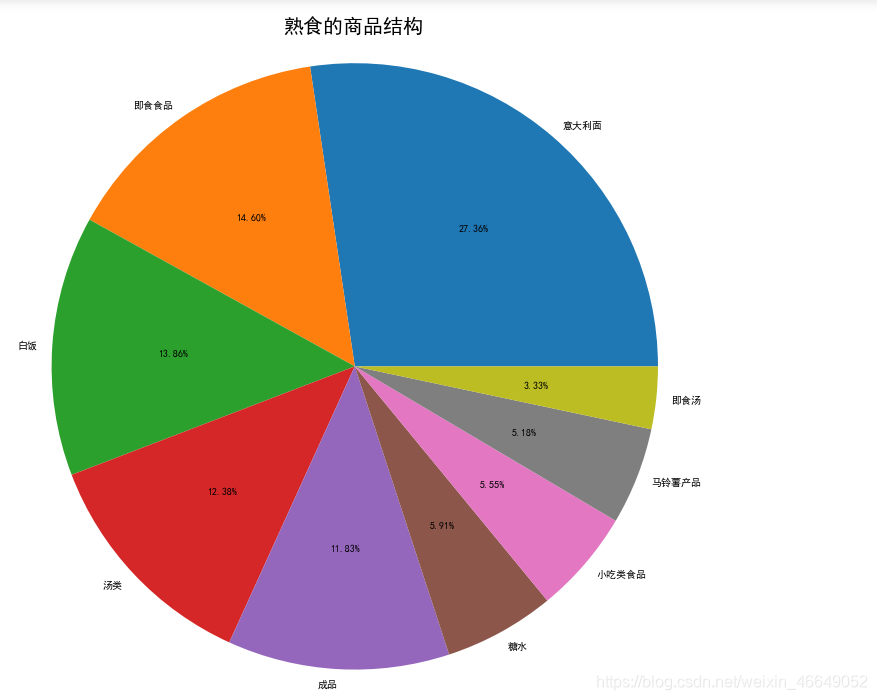
上述饼状图的重合部分可以通过参数explode、pctdistance、labeldistance来进行调整
通过上述类别商品的商品结构分析可以知道在每一类别中，哪些商品销售高，而商场就要注意这类商品的摆放位置和库存。

二、数据预处理

通过数据探索分析，我们知道了数据没有缺失值，也没有异常值。但是在使用Apriori关联分析前，需要对数据格式进行转换。

order_data = pd.read_csv('data/GoodsOrder.csv',header=0,encoding='gbk')
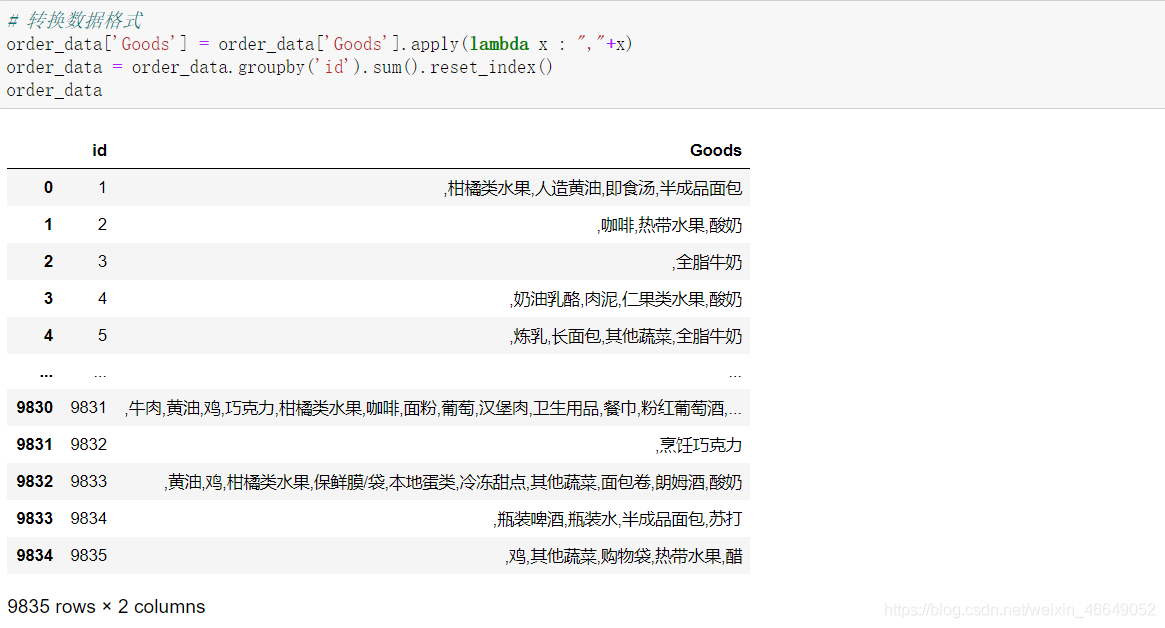
# 转换数据格式
order_data['Goods'] = order_data['Goods'].apply(lambda x : ","+x)
order_data = order_data.groupby('id').sum().reset_index()

在这里插入图片描述

order_data['Goods'] = order_data['Goods'].apply(lambda x : [x[1:]])

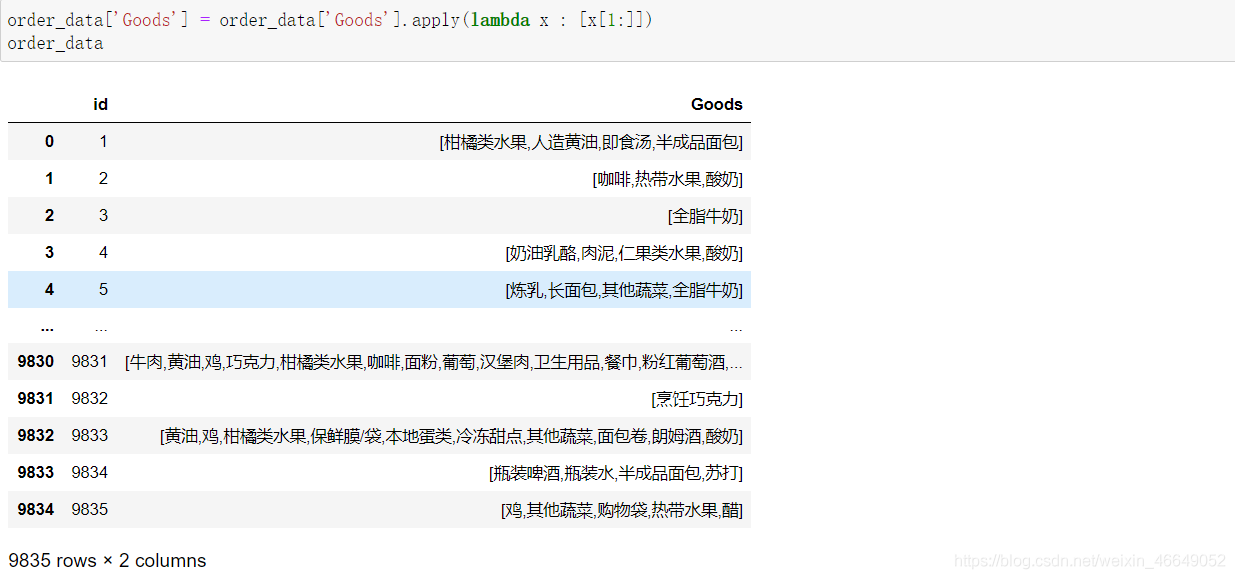
在这里插入图片描述

order_data_list = list(order_data['Goods'])
# print(order_data_list)
# 分割商品名为每一个元素
data_translation = []
for i in order_data_list:# 列表中元素为1个字符串，所以用0索引p = i[0].split(",")data_translation.append(p)
print('数据转换结果的前5个元素:\n',data_translation[0:5])

在这里插入图片描述

三、模型构建

本案例目标是探索商品之间的关联性，因此可以采用Apriori关联规则算法。
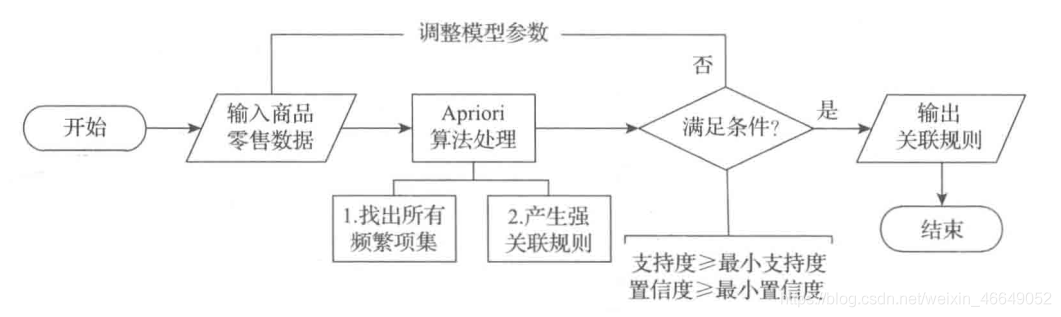
模型实现步骤如下：

设置建模参数的最小支持度与最小置信度，输入建模样本数据。按照业务经验与多次调整，这里选择最小支持度为0.02，最小置信度为0.35
采用Apriori关联规则算法对建模的样本数据进行分析，以模型参数设置的最小支持度、最小置信度作为条件，如果所有规则都不满足条件，则需要重新调整模型参数，否则输出关联规则结果

import pandas as pd# 测试数据集，用于debug
def loadDataSet():return [['a', 'c', 'e'], ['b', 'd'], ['b', 'c'], ['a', 'b', 'c', 'd'], ['a', 'b'], ['b', 'c'], ['a', 'b'],['a', 'b', 'c', 'e'], ['a', 'b', 'c'], ['a', 'c', 'e']]def loaddata():order_data = pd.read_csv('data/GoodsOrder.csv', header=0, encoding='gbk')# 转换数据格式order_data['Goods'] = order_data['Goods'].apply(lambda x: "," + x)order_data = order_data.groupby('id').sum().reset_index()order_data['Goods'] = order_data['Goods'].apply(lambda x: [x[1:]])order_data_list = list(order_data['Goods'])# print(order_data_list)# 分割商品名为每一个元素data_translation = []for i in order_data_list:# 列表中元素为1个字符串，所以用0索引p = i[0].split(",")data_translation.append(p)return data_translationdef creatC1(data):"""找到1项候选集C1:param data: 数据集:return: 1项候选集C1"""C1 = []for row in dataSet:for item in row:if [item] not in C1:C1.append([item])# 中文字符串升序排序C1.sort()# frozenset()返回一个冻结的集合，冻结后集合不能再添加或删除任何元素return list(map(frozenset, C1))def calSupport(D, C, minSupport):"""计算1项候选集的支持度,剔除小于最小支持度的项集，:param D: 数据集:param C1: 候选集:param minSupport: 最小支持度:return: 返回1项频繁集及其支持度"""dict_sup = {}  # 中间储存变量，用于计数# 迭代每一条数据，对项集中的每一项进行计数for i in D:for j in C:# 集合j是否是集合i的子集，如果是返回True，否则返回Falseif j.issubset(i):# 再判断之前有没有统计过，没有统计过的话为1if j not in dict_sup:dict_sup[j] = 1else:dict_sup[j] += 1# 事务总数sumCount = float(len(D))# 计算支持度，支持度 = 项集的计数/事务总数supportData = {}  # 用于存储频繁集的支持度relist = []  # 用于存储频繁集for i in dict_sup:temp_sup = dict_sup[i] / sumCount# 将剔除后的频繁项集及其对应支持度保存起来if temp_sup > minSupport:relist.append(i)supportData[i] = temp_sup# 返回1项频繁项集及其对应支持度return relist, supportDatadef aprioriGen(Lk, k):"""改良了剪枝步，原来的Ck是由L1与L(k-1)来连接产生的，这里采用了新的连接方式使用剪枝算法，减少了候选集空间，找到k项候选集:param Lk: k-1项频繁集:param k: 第k项:return: 第k项候选集"""reList = []  # 用来存储第k项候选集lenLk = len(Lk)  # 第k-1项频繁集的长度# 两两组合遍历for i in range(lenLk):for j in range(i + 1, lenLk):L1 = list(Lk[i])[:k - 2]L2 = list(Lk[j])[:k - 2]L1.sort()L2.sort()# 前k-1项相等，则可相乘，这样可以防止重复项出现if L1 == L2:a = Lk[i] | Lk[j]  # a为frozenset集合# 进行剪枝a1 = list(a)  # a1为k项集中的一个元素b = []  # b为它的所有k-1项子集# 构造b:遍历取出每一个元素，转换为set，依次从a1中剔除该元素，并加入到b中for q in range(len(a1)):t = [a1[q]]tt = frozenset(set(a1) - set(t))b.append(tt)# 当b都是频繁集时，则保留a1,否则，删除t = 0for w in b:# 如果为True，说明是属于候选集，否则不属于候选集if w in Lk:t += 1# 如果它的子集都为频繁集，则a1是候选集if len(b) == t:reList.append(b[0] | b[1])return reListdef scanD(D, Ck, minSupport):"""计算候选k项集的支持度，剔除小于最小支持度的候选集，得到频繁k项集及其支持度:param D: 数据集:param Ck: 候选k项集:param minSupport: 最小支持度:return: 返回频繁k项集及其支持度"""sscnt = {}  # 存储支持度for tid in D:  # 遍历数据集for can in Ck:  # 遍历候选项if can.issubset(tid):  # 判断数据集中是否含有候选集各项if can not in sscnt:sscnt[can] = 1else:sscnt[can] += 1# 计算支持度numItem = len(D)  # 事务总数reList = []  # 存储k项频繁集supportData = {}  # 存储频繁集对应支持度for key in sscnt:support = sscnt[key] / numItemif support > minSupport:reList.insert(0, key)  # 满足条件的加入Lk中supportData[key] = supportreturn reList, supportDatadef apriori(dataSet, minSupport=0.2):"""apriori关联规则算法:param data: 数据集:param minSupport: 最小支持度:return: 返回频繁集及对应的支持度"""# 首先，找到1项候选集C1 = creatC1(dataSet)# 使用list()转化为列表，用于支持度计算D = list(map(set, dataSet))# 计算1项候选集的支持度,剔除小于最小支持度的项集，返回1项频繁集及其支持度L1, supportData = calSupport(D, C1, minSupport)L = [L1]  # 加列表框，使得1项频繁集称为一个单独的元素k = 2  # k项# 跳出循环的条件是没有候选集while len(L[k - 2]) > 0:# 产生k项候选集CkCk = aprioriGen(L[k - 2], k)# 计算候选k项集的支持度，剔除小于最小支持度的候选集，得到频繁k项集及其支持度Lk, supK = scanD(D, Ck, minSupport)# 将supK中的键值对添加到supportDatasupportData.update(supK)# 将第k项的频繁集添加到L中L.append(Lk)  # L的最后一个值为空值k += 1del L[-1]# 返回频繁集及其对应的支持度；L为频繁项集，是一个列表，1,2，3项集分别为一个元素return L, supportDatadef getSubset(fromList, totalList):"""生成集合的所有子集:param fromList::param totalList:"""for i in range(len(fromList)):t = [fromList[i]]tt = frozenset(set(fromList) - set(t))  # k-1项子集if tt not in totalList:totalList.append(tt)tt = list(tt)if len(tt) > 1:getSubset(tt, totalList)  # 所有非1项子集def calcConf(freqSet, H, supportData, ruleList, minConf):"""计算置信度，并剔除小于最小置信度的数据,这里利用了提升度概念:param freqSet: k项频繁集:param H: k项频繁集对应的所有子集:param supportData: 支持度:param RuleList: 强关联规则:param minConf: 最小置信度"""# 遍历freqSet中的所有子集并计算置信度for conseq in H:conf = supportData[freqSet] / supportData[freqSet - conseq]  # 相当于把事务总数抵消了# 提升度lift计算lift=p(a&b)/p(a)*p(b)lift = supportData[freqSet] / (supportData[conseq] * supportData[freqSet - conseq])if conf >= minConf and lift > 1:print(freqSet - conseq, '-->', conseq, '支持度', round(supportData[freqSet], 6), '置信度：', round(conf, 6),'lift值为：', round(lift, 6))ruleList.append((freqSet - conseq, conseq, conf))def get_rule(L, supportData, minConf=0.7):"""生成强关联规则：频繁项集中满足最小置信度阈值，就会生成强关联规则:param L: 频繁集:param supportData: 支持度:param minConf: 最小置信度:return: 返回强关联规则"""bigRuleList = []  # 存储强关联规则# 从2项频繁集开始计算置信度for i in range(1, len(L)):for freqSet in L[i]:H1 = list(freqSet)all_subset = []  # 存储H1的所有子集# 生成所有子集getSubset(H1, all_subset)# print(all_subset)# 计算置信度，并剔除小于最小置信度的数据calcConf(freqSet, all_subset, supportData, bigRuleList, minConf)return bigRuleListif __name__ == '__main__':dataSet = loaddata()# 返回频繁集及其对应的支持度L, supportData = apriori(dataSet, minSupport=0.02)# 生成强关联规则rule = get_rule(L, supportData, minConf=0.35)

frozenset({'水果/蔬菜汁'}) --> frozenset({'全脂牛奶'}) 支持度 0.02664 置信度： 0.368495 lift值为： 1.44216
frozenset({'人造黄油'}) --> frozenset({'全脂牛奶'}) 支持度 0.024199 置信度： 0.413194 lift值为： 1.617098
frozenset({'仁果类水果'}) --> frozenset({'全脂牛奶'}) 支持度 0.030097 置信度： 0.397849 lift值为： 1.557043
frozenset({'牛肉'}) --> frozenset({'全脂牛奶'}) 支持度 0.021251 置信度： 0.405039 lift值为： 1.58518
frozenset({'冷冻蔬菜'}) --> frozenset({'全脂牛奶'}) 支持度 0.020437 置信度： 0.424947 lift值为： 1.663094
frozenset({'本地蛋类'}) --> frozenset({'其他蔬菜'}) 支持度 0.022267 置信度： 0.350962 lift值为： 1.813824
frozenset({'黄油'}) --> frozenset({'其他蔬菜'}) 支持度 0.020031 置信度： 0.361468 lift值为： 1.868122
frozenset({'本地蛋类'}) --> frozenset({'全脂牛奶'}) 支持度 0.029995 置信度： 0.472756 lift值为： 1.850203
frozenset({'黑面包'}) --> frozenset({'全脂牛奶'}) 支持度 0.025216 置信度： 0.388715 lift值为： 1.521293
frozenset({'糕点'}) --> frozenset({'全脂牛奶'}) 支持度 0.033249 置信度： 0.373714 lift值为： 1.462587
frozenset({'酸奶油'}) --> frozenset({'其他蔬菜'}) 支持度 0.028876 置信度： 0.402837 lift值为： 2.081924
frozenset({'猪肉'}) --> frozenset({'其他蔬菜'}) 支持度 0.021657 置信度： 0.375661 lift值为： 1.941476
frozenset({'酸奶油'}) --> frozenset({'全脂牛奶'}) 支持度 0.032232 置信度： 0.449645 lift值为： 1.759754
frozenset({'猪肉'}) --> frozenset({'全脂牛奶'}) 支持度 0.022166 置信度： 0.38448 lift值为： 1.504719
frozenset({'根茎类蔬菜'}) --> frozenset({'全脂牛奶'}) 支持度 0.048907 置信度： 0.448694 lift值为： 1.756031
frozenset({'根茎类蔬菜'}) --> frozenset({'其他蔬菜'}) 支持度 0.047382 置信度： 0.434701 lift值为： 2.246605
frozenset({'凝乳'}) --> frozenset({'全脂牛奶'}) 支持度 0.026131 置信度： 0.490458 lift值为： 1.919481
frozenset({'热带水果'}) --> frozenset({'全脂牛奶'}) 支持度 0.042298 置信度： 0.403101 lift值为： 1.577595
frozenset({'柑橘类水果'}) --> frozenset({'全脂牛奶'}) 支持度 0.030503 置信度： 0.36855 lift值为： 1.442377
frozenset({'黄油'}) --> frozenset({'全脂牛奶'}) 支持度 0.027555 置信度： 0.497248 lift值为： 1.946053
frozenset({'酸奶'}) --> frozenset({'全脂牛奶'}) 支持度 0.056024 置信度： 0.401603 lift值为： 1.571735
frozenset({'其他蔬菜'}) --> frozenset({'全脂牛奶'}) 支持度 0.074835 置信度： 0.386758 lift值为： 1.513634
frozenset({'全脂牛奶', '酸奶'}) --> frozenset({'其他蔬菜'}) 支持度 0.022267 置信度： 0.397459 lift值为： 2.054131
frozenset({'酸奶', '其他蔬菜'}) --> frozenset({'全脂牛奶'}) 支持度 0.022267 置信度： 0.512881 lift值为： 2.007235
frozenset({'全脂牛奶', '根茎类蔬菜'}) --> frozenset({'其他蔬菜'}) 支持度 0.023183 置信度： 0.474012 lift值为： 2.44977
frozenset({'根茎类蔬菜', '其他蔬菜'}) --> frozenset({'全脂牛奶'}) 支持度 0.023183 置信度： 0.48927 lift值为： 1.914833

使用封装好的库：

import numpy as np
import pandas as pd
import xlrd
from mlxtend.frequent_patterns import apriori  # 生成频繁项集
from mlxtend.frequent_patterns import association_rules  # 生成强关联规则
import warningswarnings.filterwarnings("ignore")  # 用于排除警告def loaddata():order_data = pd.read_csv('data/GoodsOrder.csv', header=0, encoding='gbk')# 转换数据格式order_data['Goods'] = order_data['Goods'].apply(lambda x: "," + x)order_data = order_data.groupby('id').sum().reset_index()order_data['Goods'] = order_data['Goods'].apply(lambda x: [x[1:]])order_data_list = list(order_data['Goods'])# print(order_data_list)# 分割商品名为每一个元素data_translation = []for i in order_data_list:# 列表中元素为1个字符串，所以用0索引p = i[0].split(",")data_translation.append(p)return data_translationif __name__ == '__main__':dataSet = loaddata()column_list = []for var in dataSet:column_list = set(column_list) | set(var)print('转换原数据到0-1矩阵')data = pd.DataFrame(np.zeros((len(dataSet), 169)), columns=column_list)for i in range(len(dataSet)):for j in dataSet[i]:data.loc[i, j] += 1# apriori算法frequent_itemsets = apriori(data, min_support=0.02, use_colnames=True)print(pd.DataFrame(frequent_itemsets))pd.DataFrame(frequent_itemsets).to_csv('frequent_itemsets.csv')# 生成关联准则rules = association_rules(frequent_itemsets, metric="confidence", min_threshold=0.35)print(pd.DataFrame(rules))pd.DataFrame(rules).to_csv('rules.csv')

      support             itemsets
0    0.038434                (威化饼)
1    0.026029               (一般饮料)
2    0.025826               (一般肉类)
3    0.033452           (超高温杀菌的牛奶)
4    0.064870                (黑面包)
..        ...                  ...
117  0.024301             (香肠, 苏打)
118  0.027351             (苏打, 酸奶)
119  0.021047             (苏打, 糕点)
120  0.023183  (根茎类蔬菜, 全脂牛奶, 其他蔬菜)
121  0.022267     (酸奶, 全脂牛奶, 其他蔬菜)[122 rows x 2 columns]antecedents consequents  ...  leverage  conviction
0           (黑面包)      (全脂牛奶)  ...  0.008641    1.217899
1            (猪肉)      (全脂牛奶)  ...  0.007435    1.209520
2            (猪肉)      (其他蔬菜)  ...  0.010502    1.291779
3            (牛肉)      (全脂牛奶)  ...  0.007845    1.251315
4         (根茎类蔬菜)      (全脂牛奶)  ...  0.021056    1.350401
5         (根茎类蔬菜)      (其他蔬菜)  ...  0.026291    1.426693
6        (水果/蔬菜汁)      (全脂牛奶)  ...  0.008168    1.178904
7          (其他蔬菜)      (全脂牛奶)  ...  0.025394    1.214013
8          (人造黄油)      (全脂牛奶)  ...  0.009235    1.268706
9            (凝乳)      (全脂牛奶)  ...  0.012517    1.461085
10           (黄油)      (全脂牛奶)  ...  0.013395    1.480817
11        (柑橘类水果)      (全脂牛奶)  ...  0.009355    1.179008
12         (冷冻蔬菜)      (全脂牛奶)  ...  0.008149    1.294636
13         (热带水果)      (全脂牛奶)  ...  0.015486    1.247252
14          (酸奶油)      (全脂牛奶)  ...  0.013916    1.352735
15         (本地蛋类)      (全脂牛奶)  ...  0.013783    1.412030
16           (酸奶)      (全脂牛奶)  ...  0.020379    1.244132
17           (糕点)      (全脂牛奶)  ...  0.010516    1.188729
18        (仁果类水果)      (全脂牛奶)  ...  0.010767    1.236375
19           (黄油)      (其他蔬菜)  ...  0.009308    1.263065
20          (酸奶油)      (其他蔬菜)  ...  0.015006    1.350565
21         (本地蛋类)      (其他蔬菜)  ...  0.009991    1.242619
22  (根茎类蔬菜, 全脂牛奶)      (其他蔬菜)  ...  0.013719    1.533320
23  (根茎类蔬菜, 其他蔬菜)      (全脂牛奶)  ...  0.011076    1.457687
24     (全脂牛奶, 酸奶)      (其他蔬菜)  ...  0.011427    1.338511
25     (酸奶, 其他蔬菜)      (全脂牛奶)  ...  0.011174    1.528340
[26 rows x 9 columns]

以一条数据分析为例：{‘根茎类蔬菜’}=>{其他蔬菜}支持度约为4.74%，置信度约为43.47%。说明同时购买根茎类蔬菜和其他蔬菜这两种商品的概率达43.47%，而这种情况发生的可能性约为4.74%。
从上面的关联规则中可以得出：以上的模型结果表明:顾客购买其他商品的时候会同时购买全脂牛奶。因此，商场应该根据实际情况将全脂牛奶放在顾客购买商品的必经之路上，或是放在商场显眼的位置，以方便顾客拿取。顾客同时购买其他蔬菜、根茎类蔬菜、酸奶油、猪肉、黄油、本地蛋类和多种水果的概率较高，因此商场可以考虑捆绑销售，或者适当调整商场布置，将这些商品的距离尽量拉近，从而提升顾客的购物体验。

如果对您有帮助，麻烦点赞关注，这真的对我很重要！！！如果需要互关，请评论留言！
在这里插入图片描述