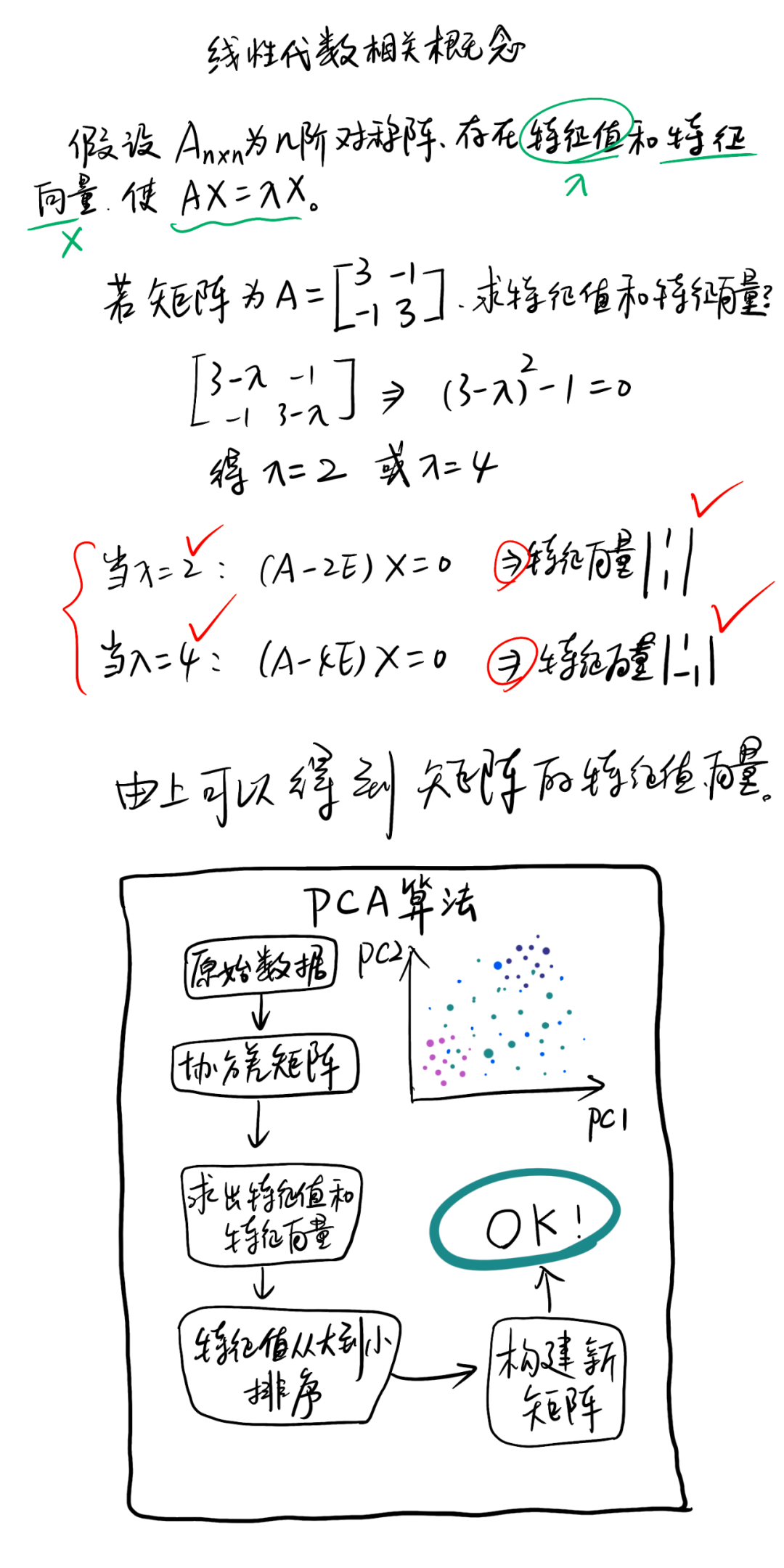
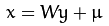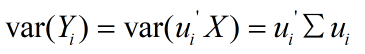一：算法概述：

主成分分析法，principle component analysis，PCA。也称主分量分析，是一种大样本，多变量数据间内在关系的一种方法。这种方法利用降维的思想，通过向量变换的方法将众多线性相关指标转换成少数线性无关的综合指标，从而切断相关的干扰，指出主导成分，作出更准确的估量。

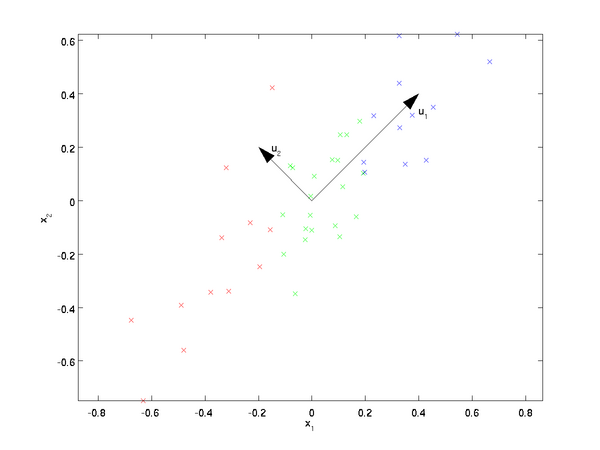
PCA在几何上表现为：将原坐标变换成新正交坐标系，使之指向样本点散步最开的p个正交方向。

在代数上表现为：将原随机向量的协方差矩阵变换成对角形阵。

二：基本原理：

PCA是一种降维的统计方法，它借助一个正交变换将其分量相关的原随机向量转化成分量不相关的新随机变量，然后对多维变量系统进行降维处理，使之能以较高精度转换成低维变量系统，再通过构造价值函数，将低维系统转化为一维系统。

记原始样本X有p个原始特征： X = (X1,X2,...,Xp)

PCA就是将这p个原始特征转变为p个特征的线性组合的问题，即原特征的线性组合Yi：

                                      

因此记                      原始特征：

                                    主成分：

                       相关系数矩阵：

                                             有Y=A·X

上式需满足：

1）主成分间不相关，即对于任意i,j，相关系数covv(Yi,Yj)=0

2）组合系数向量为单位向量：

3）各主成分方差依次递减，即var(Y1) ≥ var(Y2) ≥ ...  ≥ var(Yp)

4）总方差不变，即总信息量不变：

5）相关系数covv(Yi,Xj) = a(i,j)

6）ai是A的第i个特征向量（eigenvector），该特征向量的特征值为Yi的方差，即：

                                             

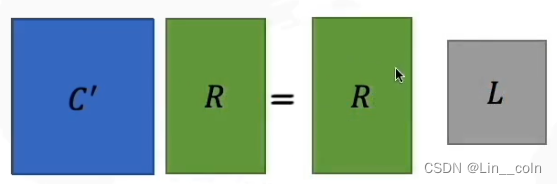
2.1 问题：A矩阵的求解？

方法：通过求解X的协方差矩阵S的特征方程，得到p个特征根和p个单位特征向量，将p个特征根按从小大到小排列分别代表p个主成分的方差，相应的单位特征向量即主成分系数。

|S-|=0，求得特征根，然后将 代入（S-)Z = 0，求得对应单位特征向量ai 以构成A矩阵

2.2 标准化处理

由于PCA根据变量离散度即方差大小确定主成分，此时不同指标的量纲不同会导致方差大小差别过大，从而影响主成分，因此需要对原变量作标准化处理：

记原样本,共计有m个样本，因此其平均值

                                  

因此对于某样本              

有标准化处理公式：

因此标准化处理后得到,对于 有协方差矩阵

对于 求得特征根 和相应的特征向量组成A。

对于相关系数 

                      

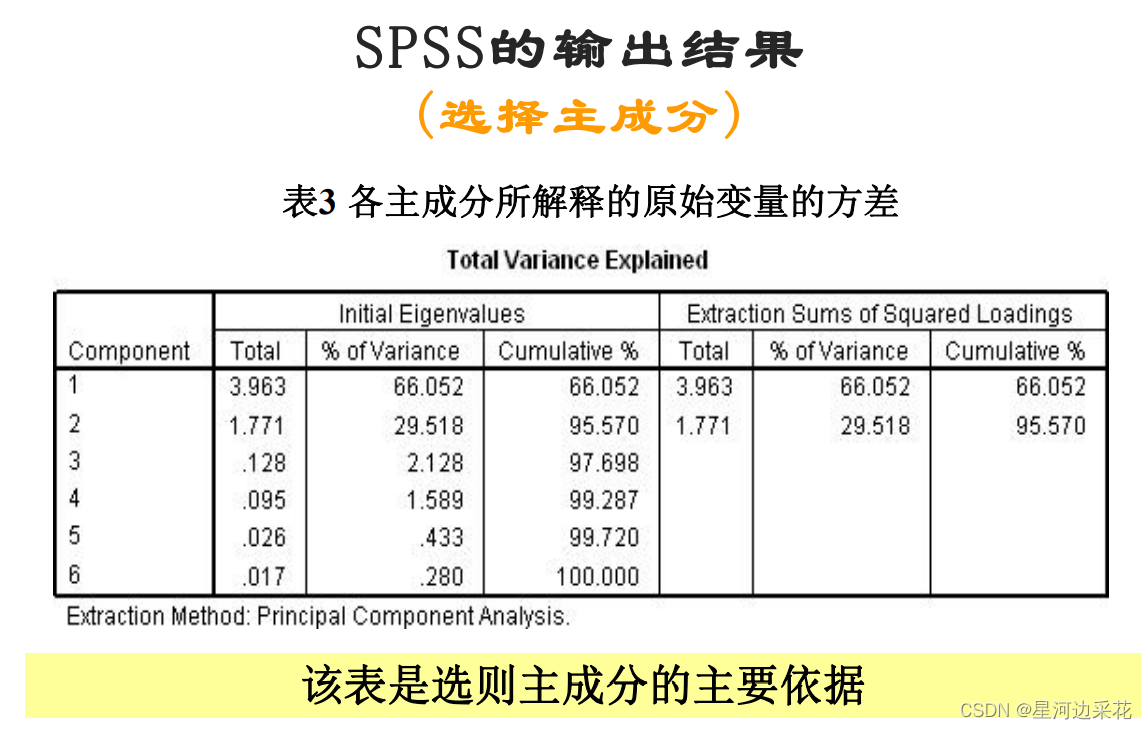
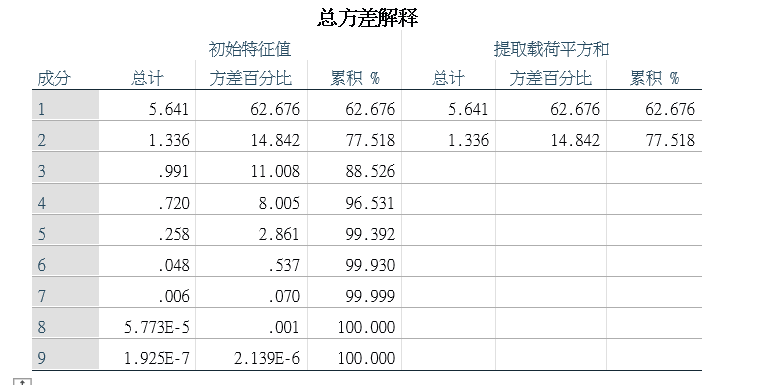
2.3 累计贡献率的k值选择

在实际问题中，利用PCA的目的是为了减少变量个数，因此在尽量少损失信息量的情况下选取前k个主成分作为主要成分

记主成分Yi的方差贡献率 ，这个值越大，说明该主成分综合原指标特征信息越强

记前K个主成分的累计贡献率为 ，其中K ≤ p

当这个累计贡献率达到指定的某个值T（比如85%）以上时，即取对应的前k个主成分，这个k个主成分基本能反映原指标信息。