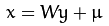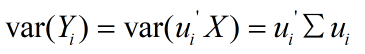【机器学习】五、主成分分析原理

在这里插入图片描述
主成分分析(Principal Component Analysis)，简称PCA，是机器学习中一种常用来进行数据降维操作的方法。PCA通过矩阵变换，将高维数据变换到低维。本文主要分享PCA的数学原理，帮助大家了解PCA降维的理论基础。码字不易，喜欢请点赞！！！

一、PCA简介
下图是一个二维的手枪图片，我们知道手枪在现实中是三维的，那为什么下面这张手枪图是二维的我们也能认出来了？这是因为虽然这张图是二维的，但是图片保留了手枪的主要特征，比如抢管、扣手等。
在这里插入图片描述
如果我们换个角度拍，比如从上向下俯视拍，你可能会认为是跟小木棍。这个原因就是我们在降低维度的过程中没有最大程度的保留他的特征，使得你无法区分。那PCA当然不希望降维之后，数据的特征完全消失，而是希望在降低维度的同时，能最大的保留数据的特征(也就是最大化的保留数据之间的差异)。

比如，我们在学校有的人有主修(Major)和辅修(Minor)专业，这个数据集是个二维的，如果想降到一维，如下图，可能会发现，往 $Feature X_1$ 方向投影之后数据的差异会大于往 $Feature X_2$ 方向投影，因此降维操作更好的选择是往 $Feature X_1$ 方向投影。
在这里插入图片描述
那这个时候又会出现一个问题，如下左图，你会发现数据往 $X_1$ 方向投影和往 $X_2$ 方向投影都不能最大化的得到数据差异，更好的方法就是采用右图中的新坐标 $Y_1$ 和 $Y_2$ ，往这个新的坐标系投影得到的结果就能很清楚的知道，我们应该选择往 $Y_1$ 方向投影，从而达到降维和保留数据差异的结果。
PS：这里坐标轴的更换就是线性代数里面的基变换。
在这里插入图片描述
更加好的一点是，在重新选择坐标系之后，还可以进行轴旋转操作，经过这两步操作之后，我们将数据之间的相关性消除了，这里又变成了特征选择了。

二、线性代数基础
这里主要讲线性代数的四个知识点，一个是内积(投影)，一个是基变换、以及特征分解和奇异值分解。

内积
假设我们有两个向量 $a=(a_1,a_2,...,a_n)^T$ 和 $b=(b_1,b_2,...,b_n)^T$ ，那么a和b的内积为：
$a·b = (a_1,a_2,...,a_n)^T·(b_1,b_2,...,b_n)^T=a_1b_1+a_2b_2+...+a_nb_n$
内积将两个向量映射为一个实数，后面我们会发现，如果一个向量的模为1，则内积其实就是另一个向量在这个向量上投影的长度。
如下图，是高中我们学习过的余弦公式，即：
$A \cdot B = ∣ A ∣ ∣ B ∣ c o s α$
其中 $∣ A ∣$ 为A的模，对于这里的二维向量， $|A|=\sqrt{x^2+y^2}$
这里假设B的模 $∣ B ∣$ 等于1，则 $A \cdot B = ∣ A ∣ c o s α$ ，表示的就是向量A在向量B上的投影。
基变换
首先，什么是基？基是刻画向量的基本工具，向量空间的任意一个元素，都可以唯一的表示成基向量的线性组合（另外，基向量的模为1）。

知道什么是基向量之后，看下面这张图，在二维中，一般来说我们将 $X_1(1,0)^T$ 和 $X_2(0,1)^T$ 作为一组基，则在这组基中的点(3,2)，其实是 $3X_1+2X_2$ 表示，那如果这里不使用 $X_1(1,0)^T$ 和 $X_2(0,1)^T$ 作为基向量，而使用 $Y_1(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})^T$ 和 $Y_2(-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})^T$ 这个向量组合作为基向量的话，则点的坐标应该为：

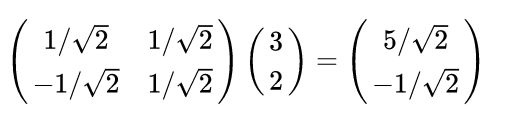
那原始基中的点(1,1)、(2,2)、(3,3)在这组基中的表示应该为：

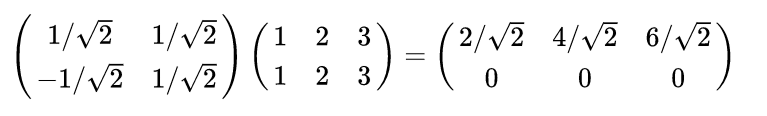
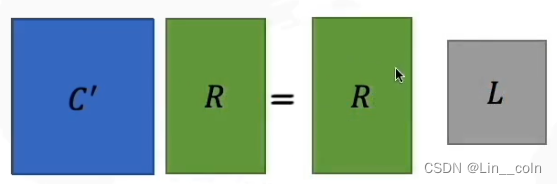
于是，我们可以得到，我们有M个N维向量，想将其变换为由R个N维向量表示的新空间中，那么首先将R个基按行组成矩阵A，然后将向量按列组成矩阵B，那么两矩阵的乘积AB就是变换结果，其中AB的第m列为A中第m列变换后的结果，即：

其中 $p_i$ 是一个行向量，表示第 $i$ 个基， $a_j$ 是一个列向量，表示第 $j$ 个原始数据记录。
特别要注意的是，这里R可以小于N，而R决定了变换后数据的维数。也就是说，我们可以将一N维数据变换到更低维度的空间中去，变换后的维度取决于基的数量。因此这种矩阵相乘的表示也可以表示降维变换。
特征分解
特征分解，在机器学习中经常出现，这里简单的说一下。
- 特征值
  如果说一个向量v是方阵A的特征向量，将一定可以表示成下面的形式：
  $Av=\lambda v$
  这时候λ就被称为特征向量v对应的特征值，一个矩阵的一组特征向量是一组正交向量。
- 特征分解
  特征值分解是将一个矩阵分解成下面的形式：
  $A=Q\Sigma Q^T$
  其中Q是这个矩阵A的特征向量组成的矩阵，正交矩阵是可逆的。 $Σ = diag(λ_1, λ_2, ..., λ_n)$ 是一个对角阵，每一个对角线上的元素就是一个特征值。
奇异值分解
特征值分解是提取矩阵特征很不错的方法，但是它只适用于方阵。而在现实的世界中，我们看到的大部分矩阵都不是方阵，比如说有M个学生，每个学生有N科成绩，这样形成的一个M * N的矩阵就可能不是方阵，我们怎样才能像描述特征值一样描述这样一般矩阵呢的重要特征呢？奇异值分解就是用来干这个事的，奇异值分解是一个能适用于任意的矩阵的一种分解的方法。

三、PCA公式推导
3.1、方法一
到现在我们已经知道通过矩阵相乘可以对数据进行降维，并且前面讲到PCA的目的是降维之后，最大程度的保留数据的特征，那么如果选择基向量矩阵，才能使变换之后的数据的特征最大程度的得以保留呢？
其实是需要两个条件：

投影之后数据的特征尽量保留，即数据的方差要越大越好
投影之后各维度之间需要线性无关，因此数据之间的协方差为0

那么到这里，我们只需要将协方差矩阵的对角线元素化为0即可，然后将对角线元素从大到小排列。假设原始协方差矩阵 $C=\frac{1}{m}XX^T$ ，并且 $Y = P X$ ，则有：

$S=\frac{1}{m}YY^T=\frac{1}{m}(PX)(PX)^T=\frac{1}{m}PXX^TP^T=\frac{1}{m}P(XX^T)P^T$

对 $XX^T$ 进行特征分解，得到 $XX^T=QDQ^T$ ，其中Q为特征分解产生的特征向量组成的向量，而D是特征值组成的对角阵。带入上式得到：

$S=\frac{1}{m}YY^T=\frac{1}{m}P(XX^T)P^T=\frac{1}{m}PQDQ^TP^T=(PQ)D(PQ)^T$

到这里，如何保证 $YY^T$ 的结果为一个对称矩阵呢，即只要上面公式可以特征分解即可，我们知道D为 $XX^T$ 的特征值组成的向量，那么这里最简单的方法就是假设 $(P Q) = I$ ，则可以保证 $YY^T$ 的结果为一个对称矩阵。即 $P=Q^T$ 。

这里我们就得到PCA的过程了，由于Q是 $XX^T$ 特征向量组成的，因此降维到k维时，找到 $XX^T$ 最大的k个特征值对应的特征向量，然后就可以得到变换矩阵P，从而得到降维之后的数据。

3.2、方法二
现在使用另外一种分析思路，得到相同的结果。
如下图，我们要将 $x_k$ 投影到向量 $e$ 上得到 $x_k^、$ ，其中 $α_k$ 表示的是投影之后的长度，则有：
$α_k=e^Tx_k$
且假设向量：
$∣ ∣ e ∣ ∣ = 1$ 。
则：
$x_k^、=α_ke$
在这里插入图片描述
我们可以理解这个过程中距离越短，则数据特征损失越少，则目标函数为：
$minJ(e)=\sum_{i=1}^n||x_k^、-x_k||^2$
由于：

由于 $x$ 已知，因此假设 $S=\sum_{i=1}^nx_kx_k^T$ ，则目标函数为：

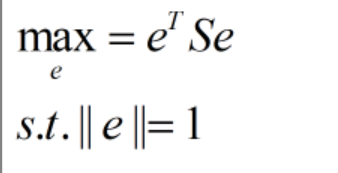
到这里，就可以采用拉格朗日乘子法求解了：
在这里插入图片描述
由于 $Se=\lambda e$ ，因此 $\lambda$ 就是 $S=XX^T$ 的特征值，所以，我们得到了同样的结论。

至此完成了PCA的数学原理推导。

四、PCA缺陷
上面我们介绍PCA的时候，你可能会发现一个问题，如果我们对数据降维之后需要做分类预测，但是PCA对数据降维的过程中，没有考虑到数据类别的问题。这可能造成数据在降维之后无法区分类别了。
比如下图，如果往 $Y$ 轴方向降维，降维之后会发现无法区分数据。那能否做到让数据按照分类降维呢？答案是可以的，使用线性判别分析(LDA)方法即可，下一次我们将分享LDA降维方法。
在这里插入图片描述

参考资料：
https://blog.csdn.net/xiaojidan2011/article/details/11595869
https://www.bilibili.com/video/av38471473/?p=6&t=1353
https://www.cnblogs.com/fuleying/p/4466326.html
https://blog.csdn.net/jinshengtao/article/details/18448355