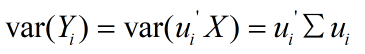[ 0 ] 一句话定义

主成分分析(principal component analysis,PCA) 是一种常用的无监督学习方法，它利用正交变换把由线性相关变量表示的观测数据转换为少数几个由线性无关变量表示的数据，线性无关的变量叫主成分，主成分个数主一般小于原始变量个数，所以它是一种降维方法。主成分分析主要用于发现数据中的基本结构，即数据中变量之间的基本关系，是一种描述性统计方法，常常用于其他机器学习方法的前处理。
——李航《统计学习方法》

[ 1 ] 使用目的和使用条件

统计分析中，变量之间可能存在相关性，以致增加了分析的难度，因而人们探索 降维 的可能性，用原始变量构造少数变量来代替多数变量，这样能保留数据中的大部分信息，同时简化了运算。

讨论： 为什么要降维/处理相关性？相关的数据难处理在哪？

从数据的意义上：举例来说，关于国家的描述有以下变量：人均收入、外汇储备、进出口贸易额等变量，这些变量不独立，反而可能十分相关，其中一个变量的自身变化往往伴随着其他变量不可忽略的变化，谈论单独某个变量对国家特征的单独贡献就没有意义，它们有着“集体贡献”，而总的贡献不是单独变量贡献之和。

从机器学习角度：要处理的数据可能有成百上千的变量，里面有与问题无关的变量，也有彼此相关的冗余变量，进行数据降维能够在较好地描述原始数据的基础上，减少计算时间，改善整体性能。机器学习的降维有两大类：
（1）特征选择：选择原始变量集的子集，不产生新的变量
（2）特征降维：生成了新的变量，如PCA

如上所述，PCA的使用条件就是变量之间存在相关性，如果是完全独立的，那么就没有做PCA的必要了。

[ 2 ] 基本思想和直观理解

把给定的一组变量 $X_1,X_2,...,X_p$ 通过线性变换转化为一组不相关的变量 $Y_1,Y_2,...,Y_p$，保持总方差不变，其中 $Y_1$ 具有最大方差，称为第一主成分，类似地，有第二、第三…第p主成分。方差表示在新变量上信息的大小。

为了直观展示，假设两维的情况。左图由于两个变量相关，呈现一个椭圆的形状，沿椭圆长轴方向包含更多的信息，即方差最大的方向，而短轴方向方差较小。右图是两个不相关变量，长短轴没有差别，近似于一个正圆，因而降维没有什么意义，因为无论向那个方向投影都不会有大的差别。

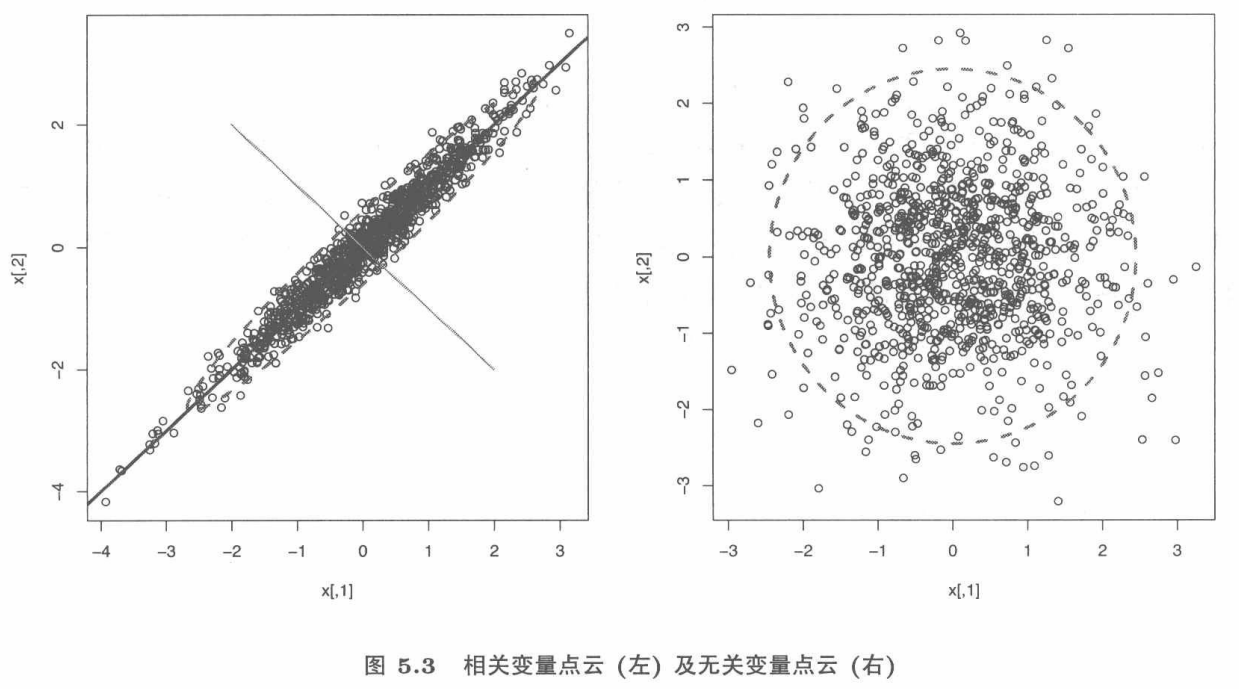
下面介绍具体的步骤，现在总结要关注的几个问题：

• 如何将原始变量变换称线性无关的变量？
• 这些成分代表了原来的多少信息？
• 是否有可能解释这些成分？

[ 3 ] 具体计算步骤

我将省略一些推导和具体的计算，尽量表达出这个过程的思路，使得不需要太好的数学基础也能尽可能看懂。

目标：$\mathbf{x}=(x_1，x_2,...,x_p{)}^T$ 是 $p$ 维随机变量，定义一个线性变换 $$y_i={\alpha }_i^T\mathbf{x}={\alpha }_{1i}{x}_1+{\alpha }_{2i}{x}_2+...+{\alpha }_{pi}{x}_p$$其中，${\alpha }_i^T=({\alpha }_{1i},{\alpha }_{2i},...,{\alpha }_{pi})$，从而将 $\mathbf{x}$ 转变为 $p$ 维随机变量 $\mathbf{y}$，使得满足以下条件：

• 系数向量 ${\alpha }_i^T$ 是单位向量，即${\alpha }_i^T{\alpha }_i=1$
• 变量 $y_i$与$y_j$互不相关
• $y_1$是 $x$所有线性变换中方差最大的，$y_2$是与$y_1$不相关的$x$的所有线性变换中方差最大的……$y_i$是与$y_1,y_2,...,y_{i-1}$都不相关的$x$的所有线性变换中方差最大的

第一个条件表明线性变换是 正交变换，${\alpha }_1,{\alpha }_2,...,{\alpha }_p$是一组标准正交基，第二、三个条件给出了求主成分的方法。那么，再具体一点，怎么求呢？

先要介绍一个定理：

设 $\mathbf{x}$ 是 $p$ 维随机变量，$\Sigma$ 是 $\mathbf{x}$ 的协方差矩阵，$\Sigma$ 的特征值分别是 ${\lambda }_1\ge {\lambda }_2\ge ...\ge {\lambda }_p$，特征值对应的单位特征向量分别是 ${\alpha }_1,{\alpha }_2,...,{\alpha }_m$，则 $\mathbf{x}$ 的第 $k$ 主成分是 $$y_k={\alpha }_k^T\mathbf{x}={\alpha }_{1k}{x}_1+{\alpha }_{2k}{x}_2+...+{\alpha }_{mk}{x}_m$$ $\mathbf{x}$的第 $k$ 主成分的方差是 $$var(y_k)={\alpha }_k^T\Sigma {\alpha }_k={\lambda }_k$$即协方差矩阵 $\Sigma$ 的第 $k$个特征值。

这个定理给出了求主成分的方法，即第一主成分 $y_1={\alpha }_1^T\mathbf{x}$， 只要求出系数向量 ${\alpha }_1$即可。而求解${\alpha }_1$是一个约束最优化问题，可以表达成如下形式，然后用拉格朗日乘子法求解。

$$\underset{{\alpha }_1}{\max }{\alpha }_1^T\Sigma {\alpha }_1$$$$s.t.{\alpha }_1^T{\alpha }_1=1$$同理，求第二主成分可以表达成以下约束最优化问题：$$\underset{{\alpha }_2}{\max }{\alpha }_2^T\Sigma {\alpha }_2$$$$s.t.{\alpha }_1^T\Sigma {\alpha }_2=0,{\alpha }_2^T\Sigma {\alpha }_1=0$$$${\alpha }_2^T{\alpha }_2=1$$ 这样就能够计算出所有的系数向量了，求解的过程在此省略。

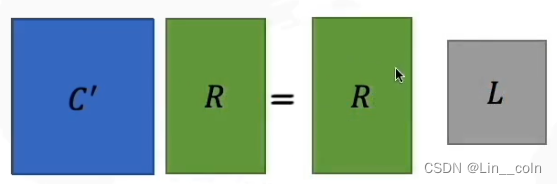
注：实际问题中，由于变量的协方差矩阵未知，因而可以用样本协方差矩阵代替，同时为了避免受到量纲的影响，通常用样本相关阵$\mathbf{R}$ 代替样本协方差矩阵，这等价于用标准化数据的协方差矩阵（标准化后的数据各个变量的均值为0，方差为1）。

这里规定一些符号：

[ 4 ] 求各个成分的累计贡献率

一个成分的重要程度由其方差占总方差的比例来衡量。对于第 $i$ 个成分，其方差为特征值 ${\lambda }_i$(由上面的定理得到)，总方差为 ${\sum }_{i=1}^p{\lambda }_i$，则第 $i$ 个成分贡献率为 ${\lambda }_i/{\sum }_{i=1}^p{\lambda }_i$

若使用样本相关阵，则计算出的特征向量 ${\mathbf{a}}_{\mathbf{i}}$ 都是单位向量，第 $i$ 个主成分和第 $j$ 个原始变量之间的相关系数为 $\sqrt{l_i}{a}_{ij}$，也就是—>

【第 $i$ 个特征向量 ${\mathbf{a}}_{\mathbf{i}}$】与【相应的特征值的平方根$\sqrt{l_i}$ 】的乘积 的各个分量为【第 $i$ 个主成分和各个原始变量之间的相关系数】

一些软件将 $\sqrt{l_i}{\mathbf{a}}_{\mathbf{i}}$ 定义为载荷，而有的将单位特征向量 ${\mathbf{a}}_i$ 定义为载荷。所谓 “载荷” 就是 “变量在主成分上的载荷”，也就是原始变量与主成分之间的相关系数。

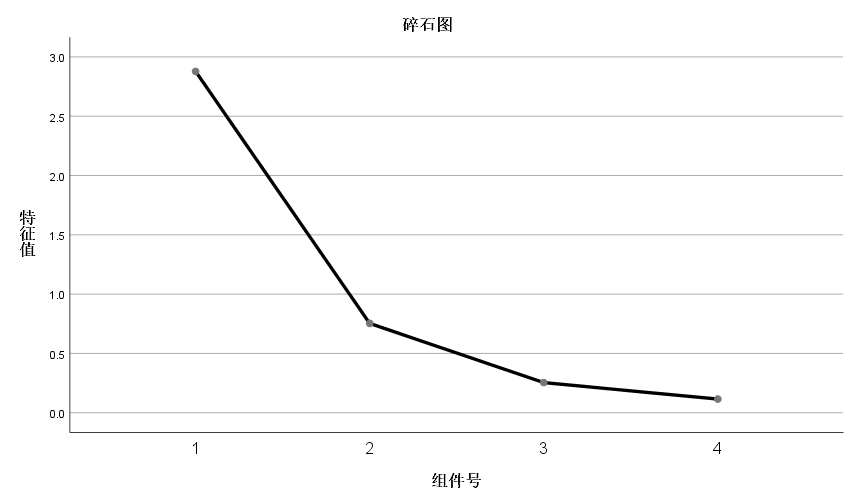
这里有两个常用的工具：碎石图和载荷图。

碎石图描述了各个成分的贡献率及累计贡献率的变化。

载荷图描述主成分和原始变量的相关系数，每一点的横坐标为相应变量和第一主成分的相关系数，纵坐标为其与第二主成分的相关系数。

[ 5 ] 主成分分析的SPSS和Python实现

SPSS实现

相关设置

【分析】—【降维】—【因子分析】— 选择变量

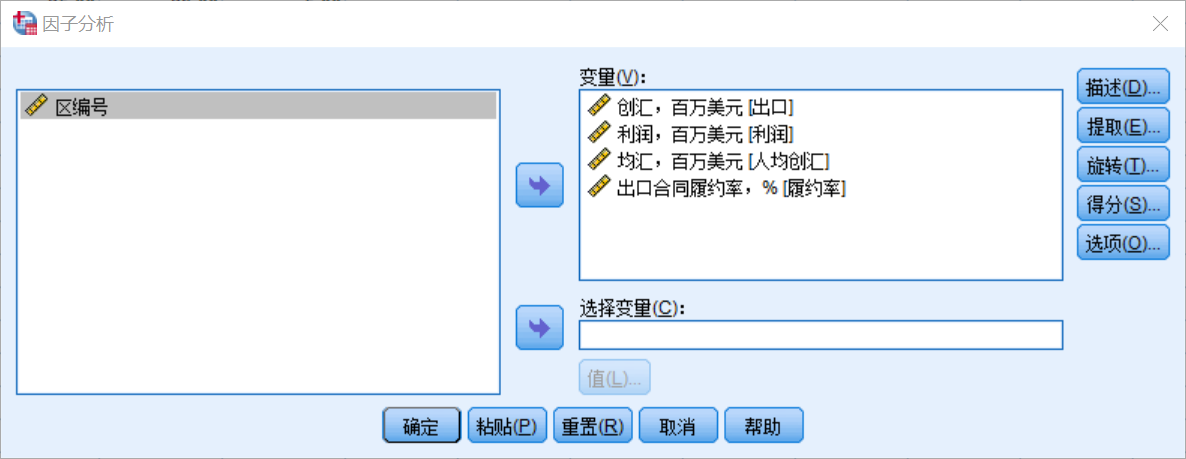
结果分析

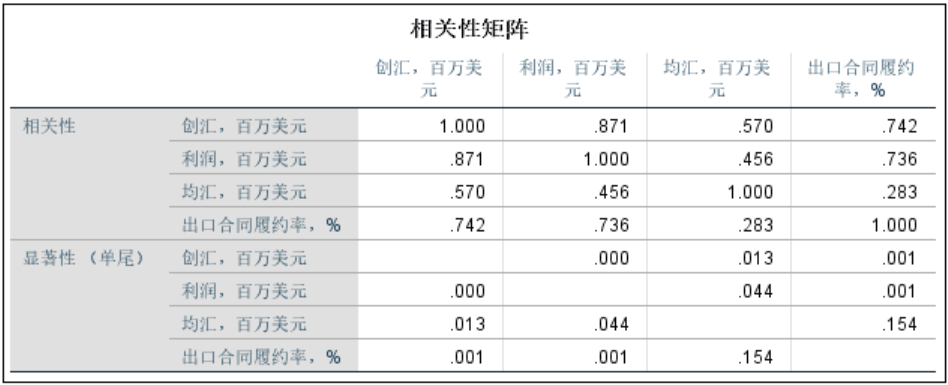
相关性矩阵描述变量之间的相关性，例如利润和创汇之间相关性很高，相关系数为0.871.

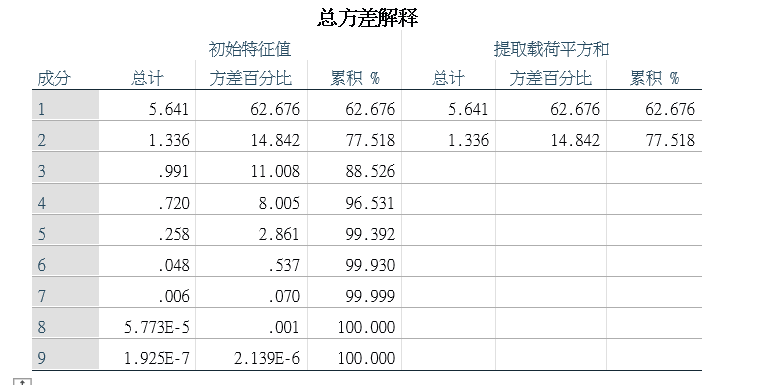
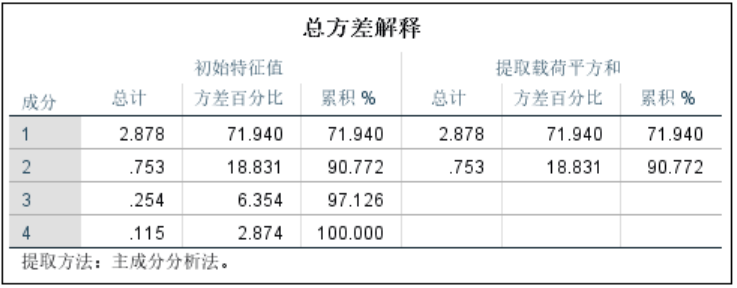
提取出四个主成分，前两个主成分的方差解释率已经达到了90.772%，保留了大部分的信息。

Python实现

import pandas as pd
import numpy as np
from sklearn.decomposition import PCAdata=pd.read_csv(r'C:\Users\Lenovo\Desktop\PCA.csv')X=np.array(data)pca=PCA(n_components=2)   # 设置主成分个数为2
pca.fit(X)    
print(pca.explained_variance_ratio_) # 输出前两个主成分的方差贡献率

[ 6 ] 总结

如果有一组数据，一共有 k 个变量，对其进行主成分分析，一般过程应当是：

1. z-score标准化，消除量纲的影响
2. 求出变量之间的相关系数矩阵 $R_{k\times k}$
3. 求R的特征根，并按从大到小排列 ${\lambda }_1,{\lambda }_2,...{\lambda }_k$，并求出其一组长度为1，相互正交的特征向量 $b_1,b_2,...,b_k$
4. 取 ${\lambda }_1,{\lambda }_2,...{\lambda }_q(q<k)$，计算 $Y_1=b_1{X}^T,....,Y_q=b_q{X}^T$，即为所求