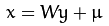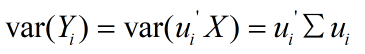Principal Component Analysis 主成分分析
地址:https://www.bilibili.com/video/BV1E5411E71z?spm_id_from=333.337.search-card.all.click

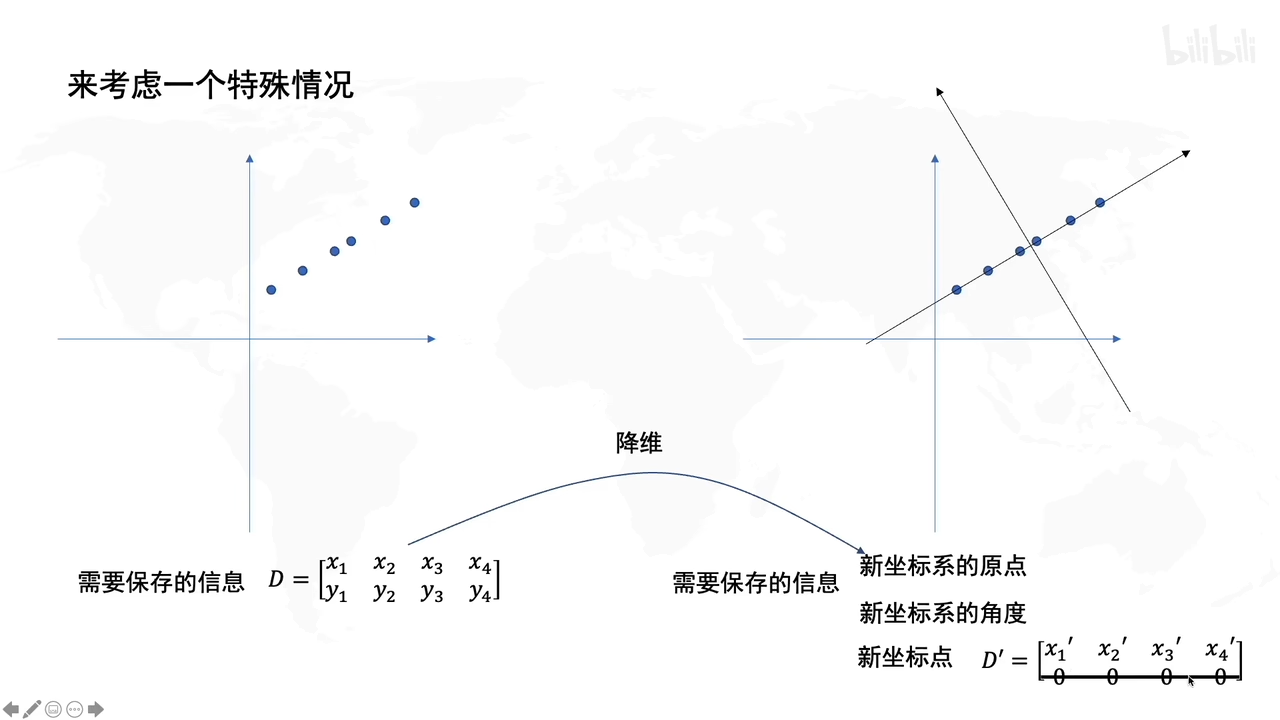
假设要保存二维的信息,由于降维考虑,期望只存储一个维度的信息(为了减少存储的信息量)

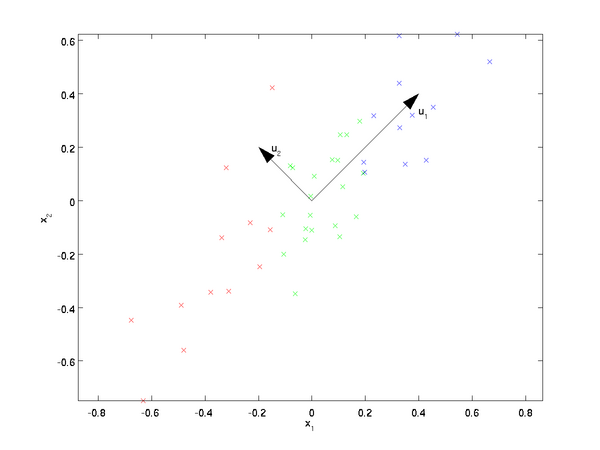
PCA是找到一个新的坐标系去存储一维信息。这个坐标系的原点落在数据的中心,坐标系的方向是往数据分布的方向上走,这样子就是降维了。
原始的数据点是蓝色的点,红色的点是蓝色的点投影到轴上的。这样通过某一些角度,只保留一维信息就能存储二维的信息量了(当然也存在信息损失,但此时目的是为了降维信息的情况下另信息损失度最小)
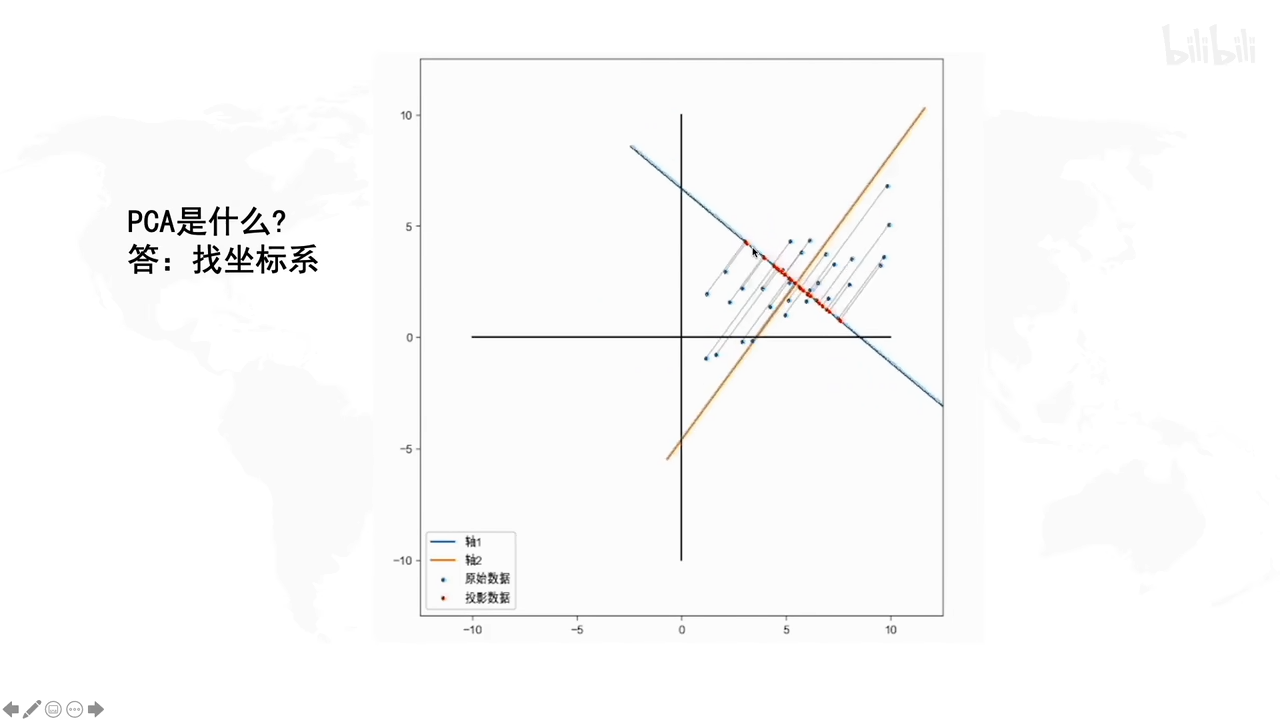
在上图就是很好的显示了,因为坐标点投影得比较分散,易于显示。
若发现投影后数据集中在一个点红色的斑点的话,说明没有保存多少信息,因为信息重合混淆了,数据不能很好地在新坐标系下区分开。
那怎么样才算好的坐标系呢?
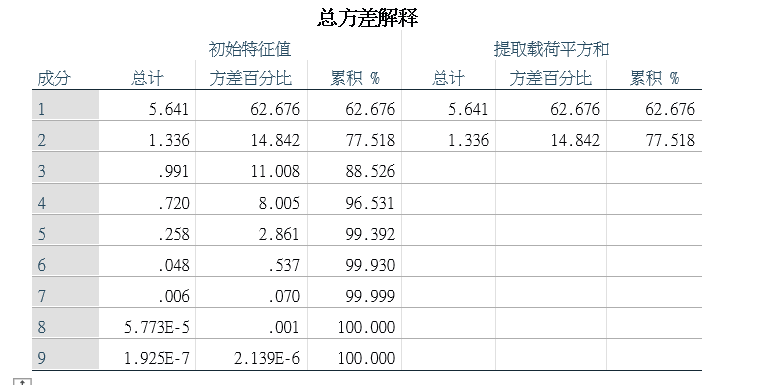
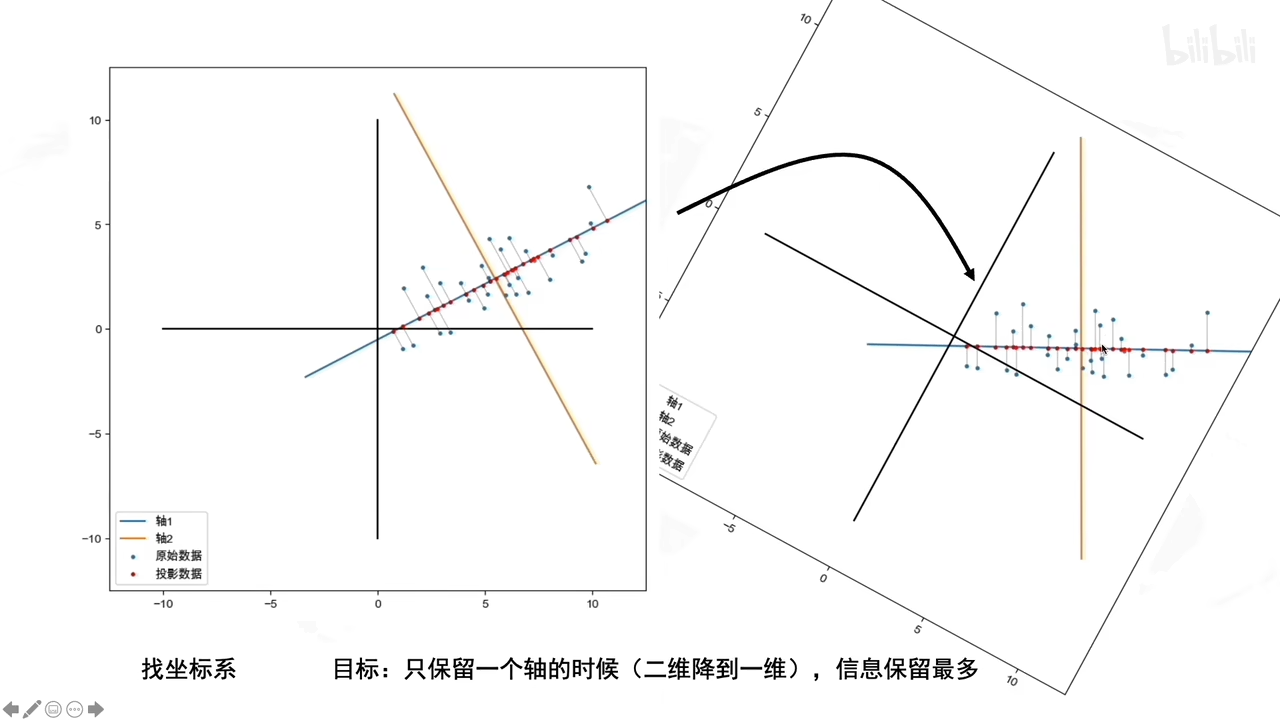
具体步骤:

若没有去中心化直接找坐标系,就会:发现不了一个好的方向让数据投影在新坐标系上分散开来。
数学思想:
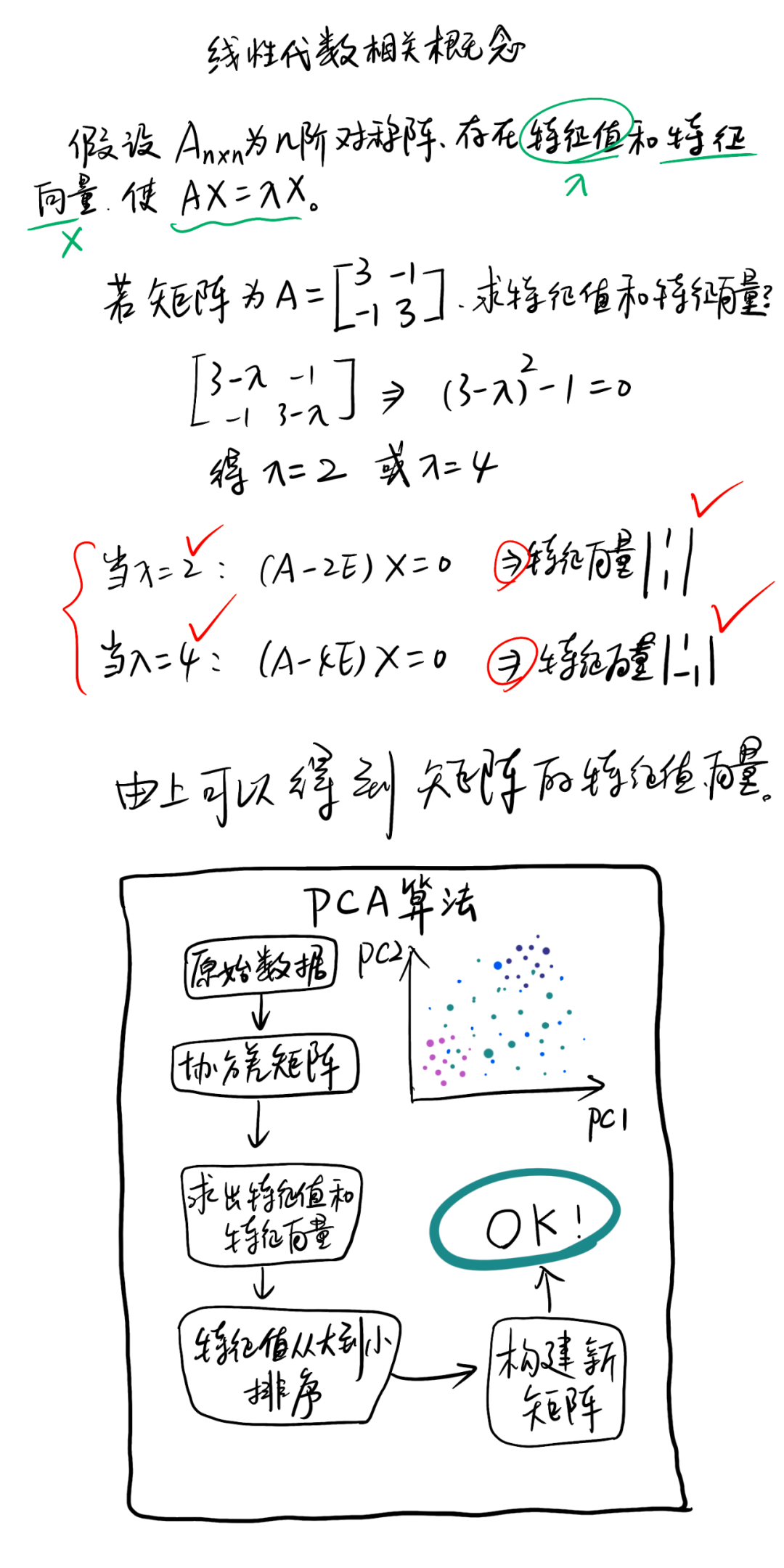
利用线代里的线性变化
拉伸操作:
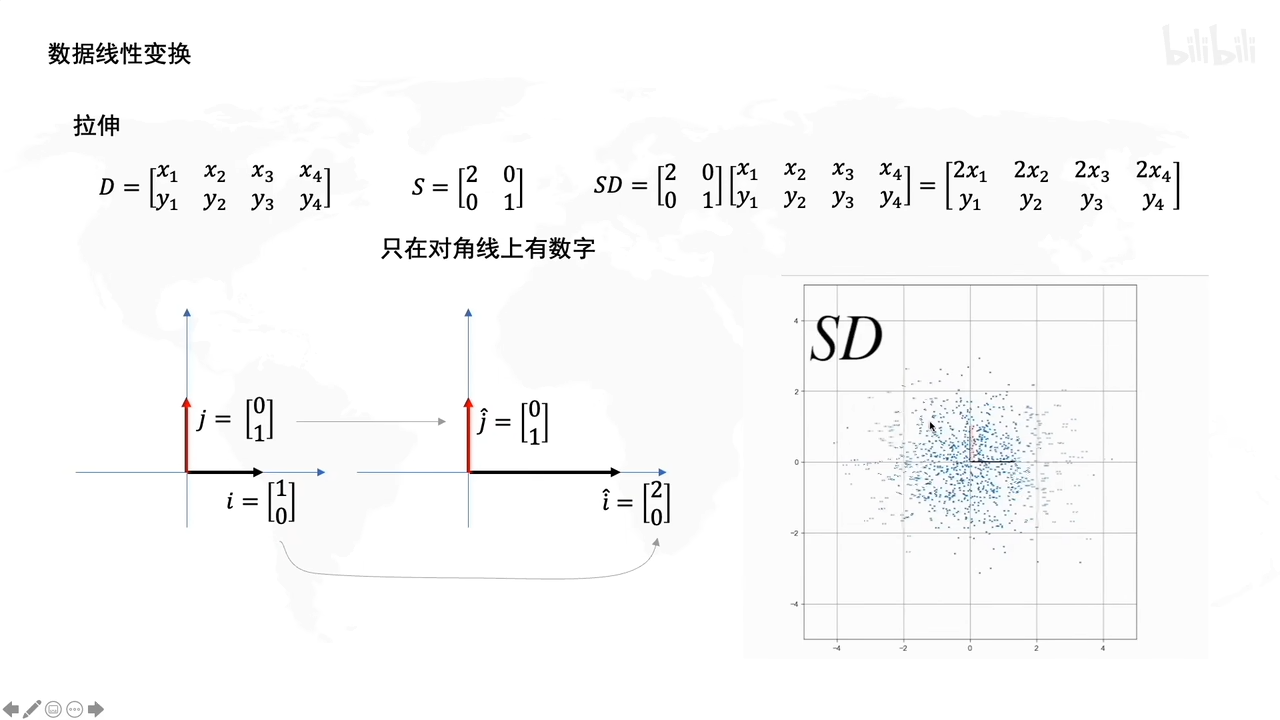
比如这里,D是一个数据集,S表示拉伸的矩阵(为了实现数据拉伸的)
S左乘D之后,相当于把D上的数据点拉伸了。
旋转操作:
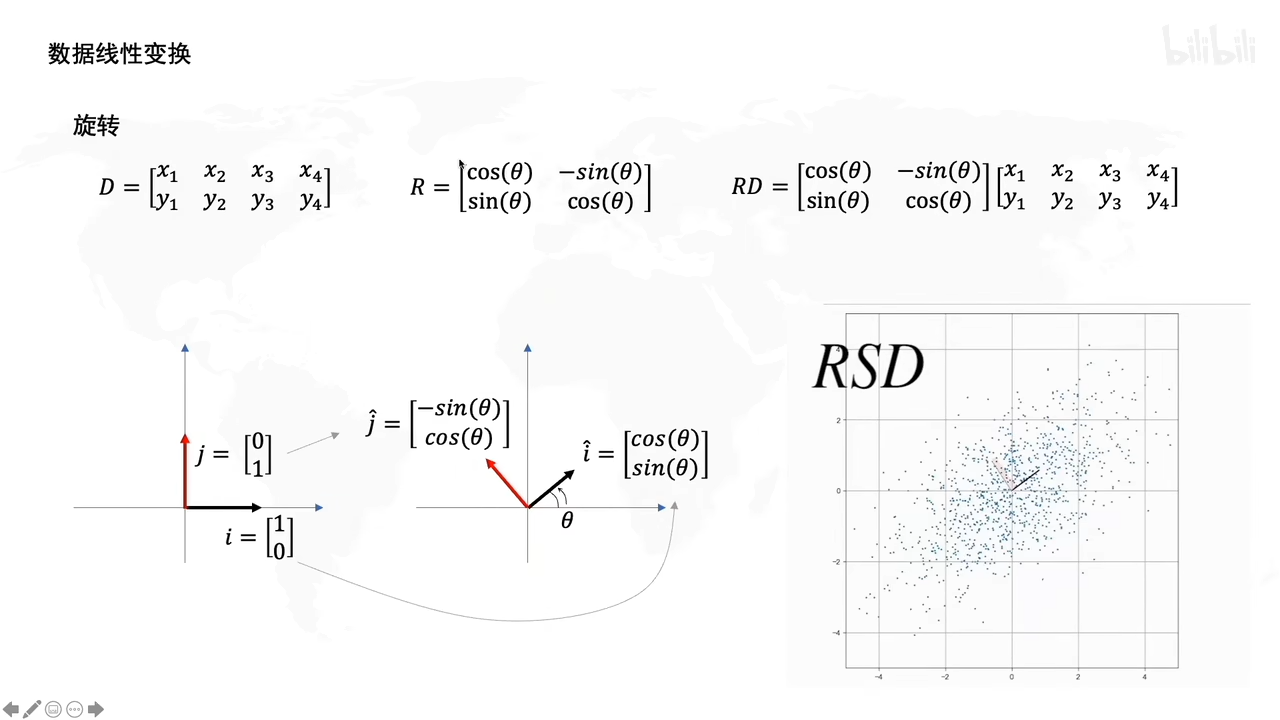
R就是个旋转矩阵,R左乘D后,让D旋转了某个角度。
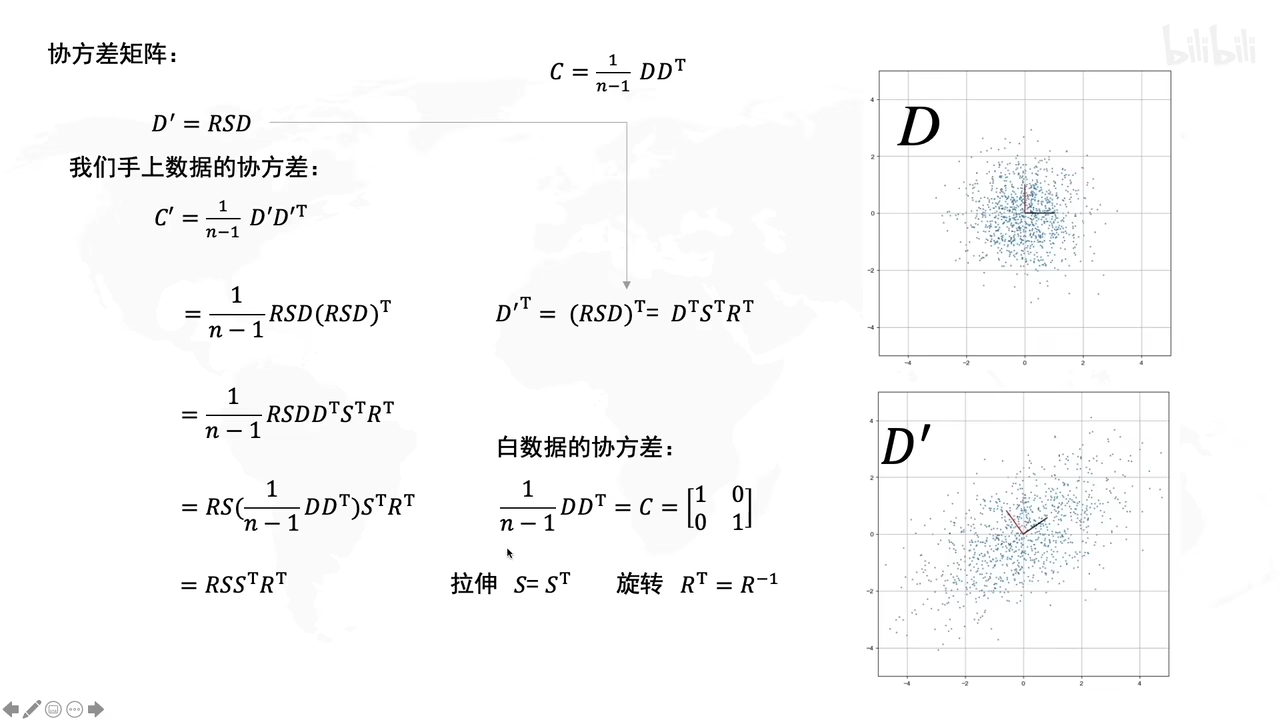
白数据的处理:
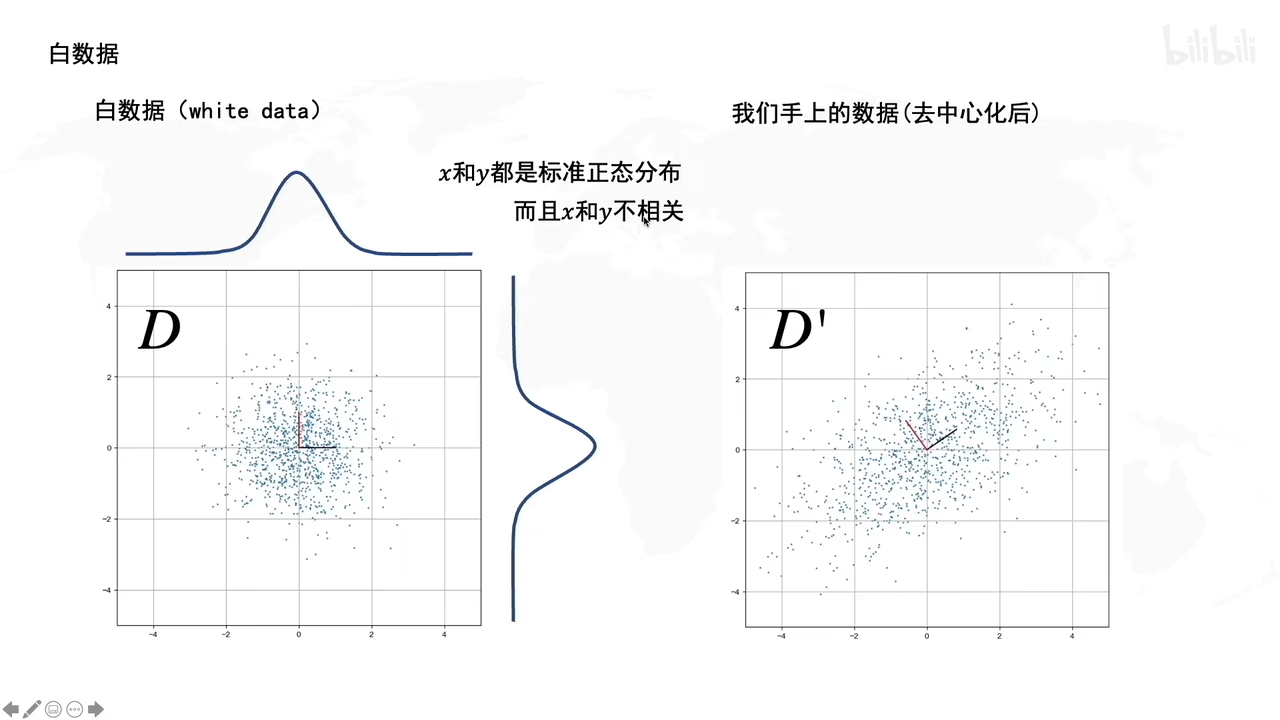
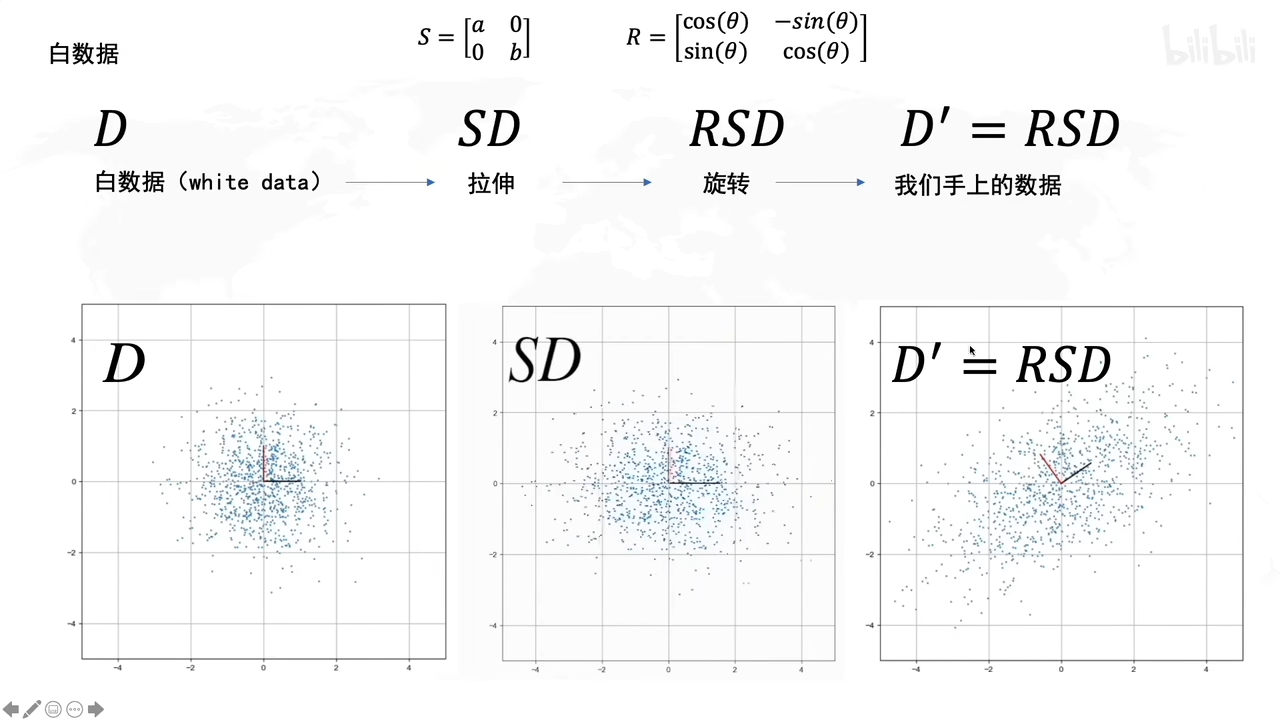
拉伸,旋转有什么作用呢?
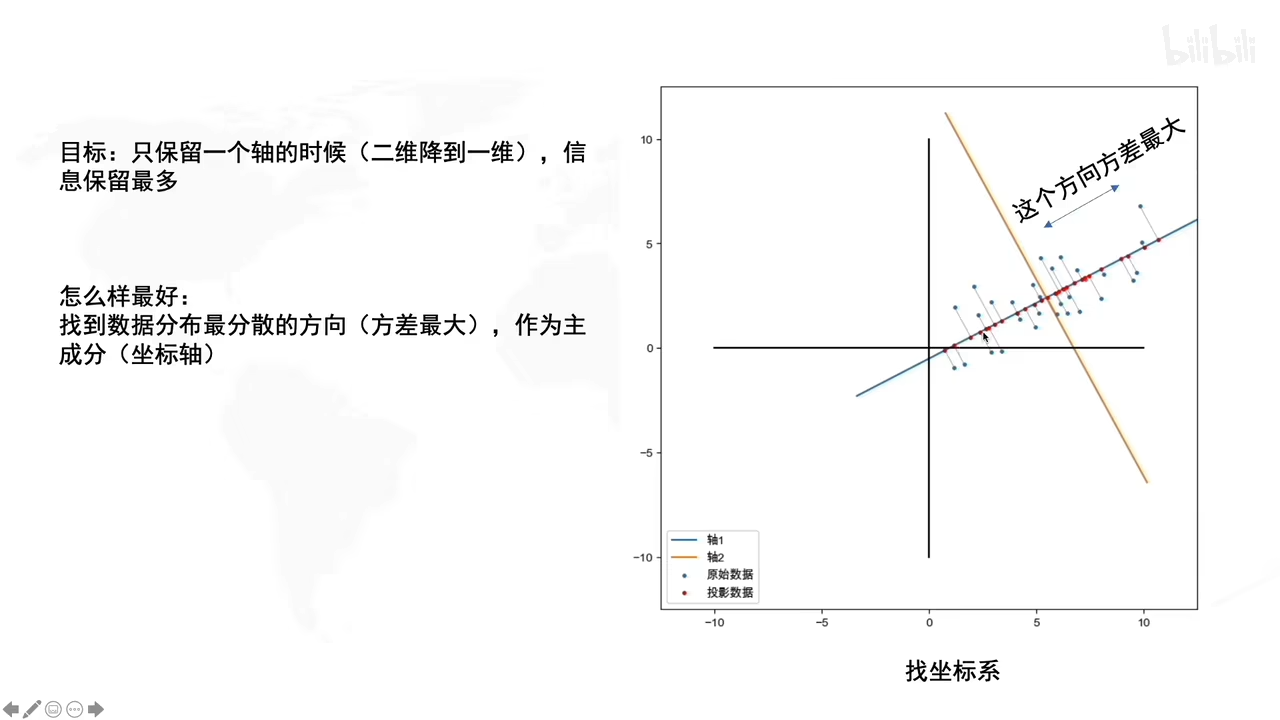
拉伸的时候,就说明了拉伸是方差最大的方向
旋转的时候决定了方差最大的方向的角度是多大
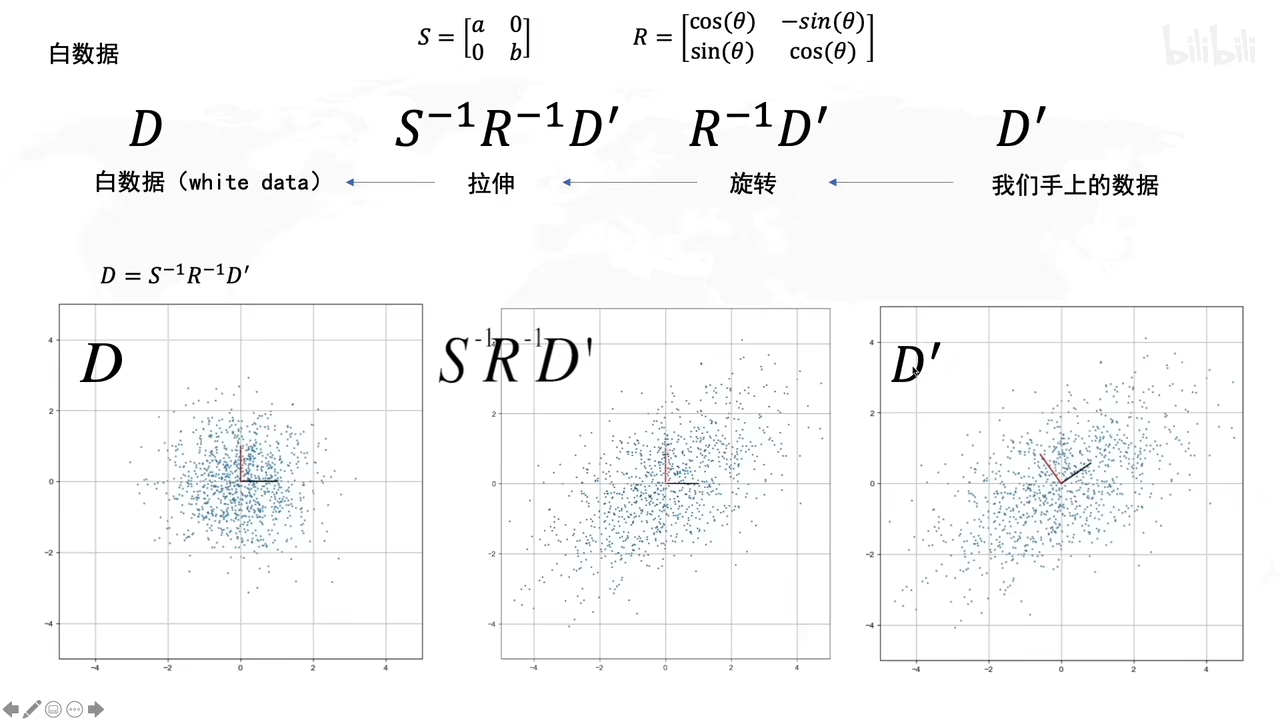
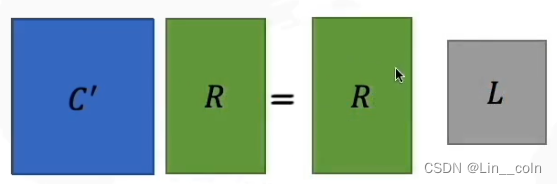
D’转化成原先矩阵D,就用各自的逆矩阵乘回来。
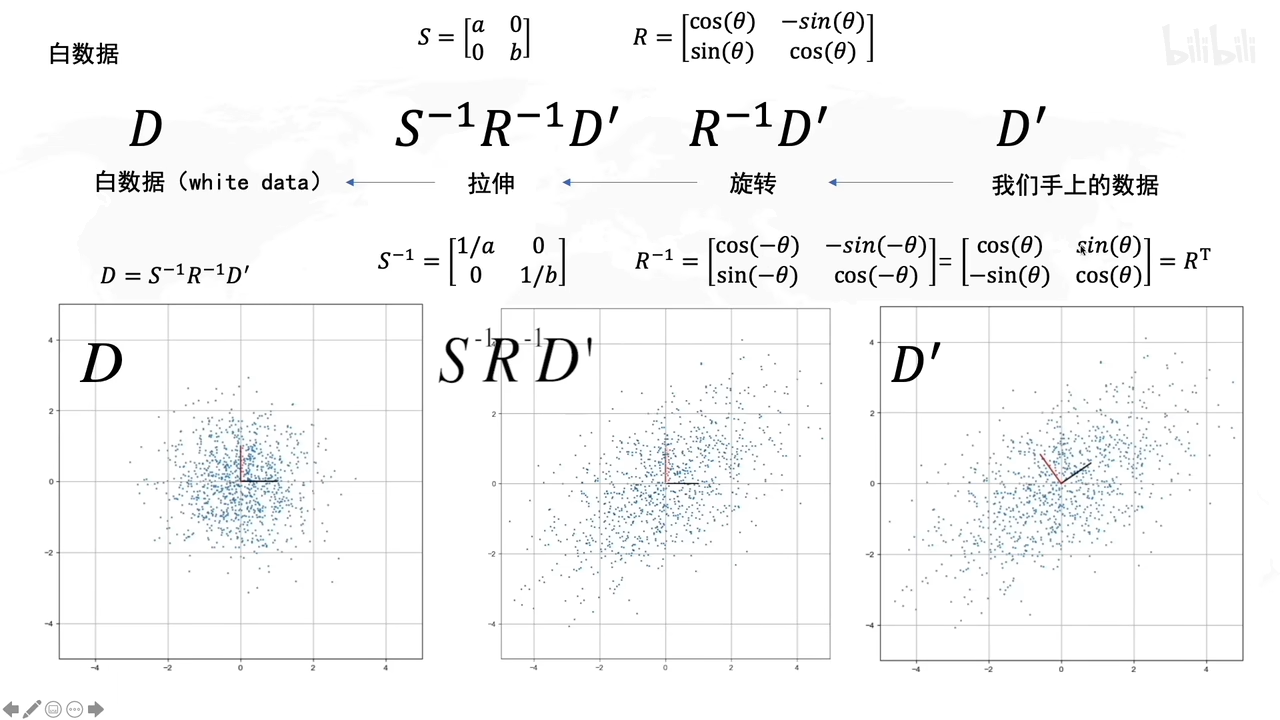
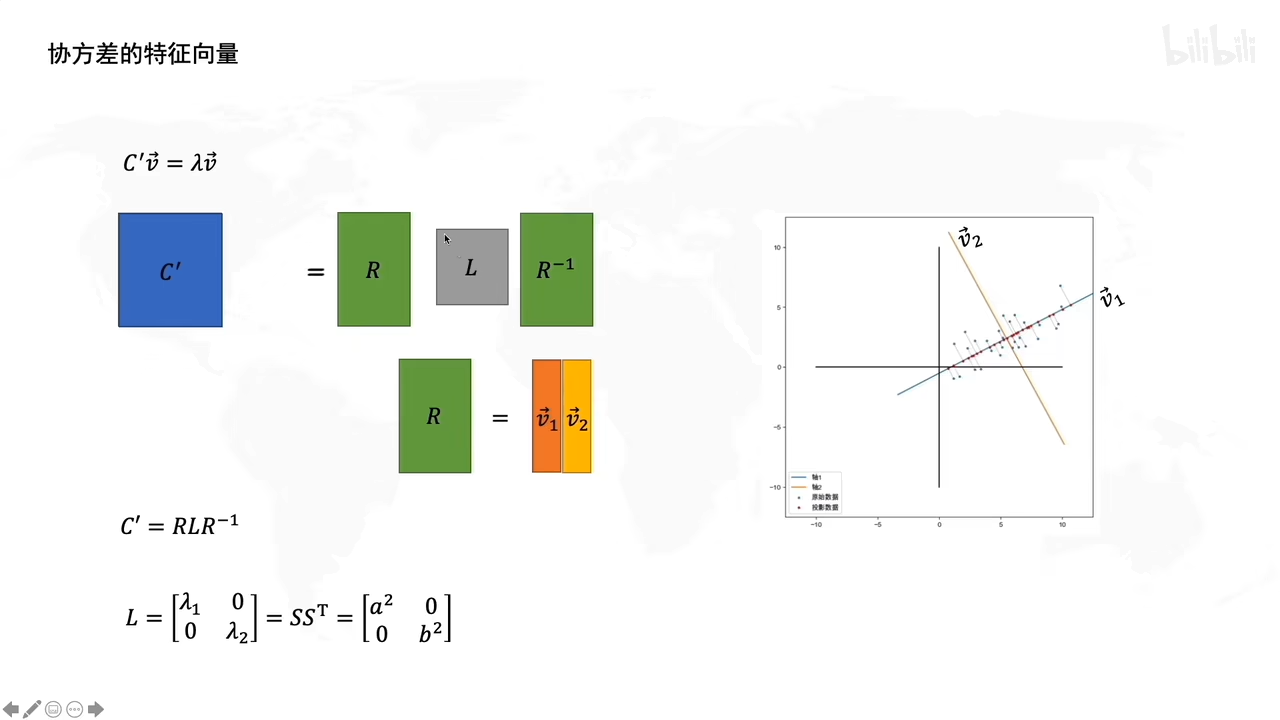
怎么求R呢
协方差的特征向量就是R
啥是协方差?
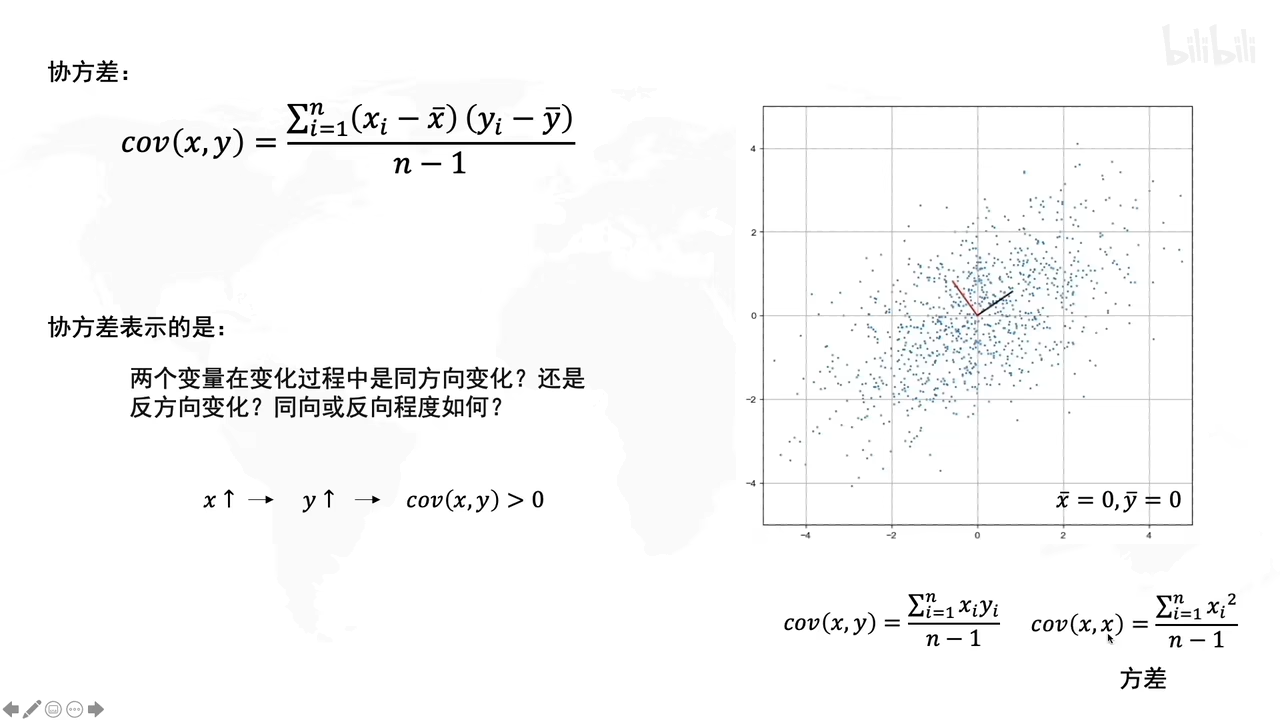
(此时是已经去中心化后的操作)
协方差矩阵是啥?
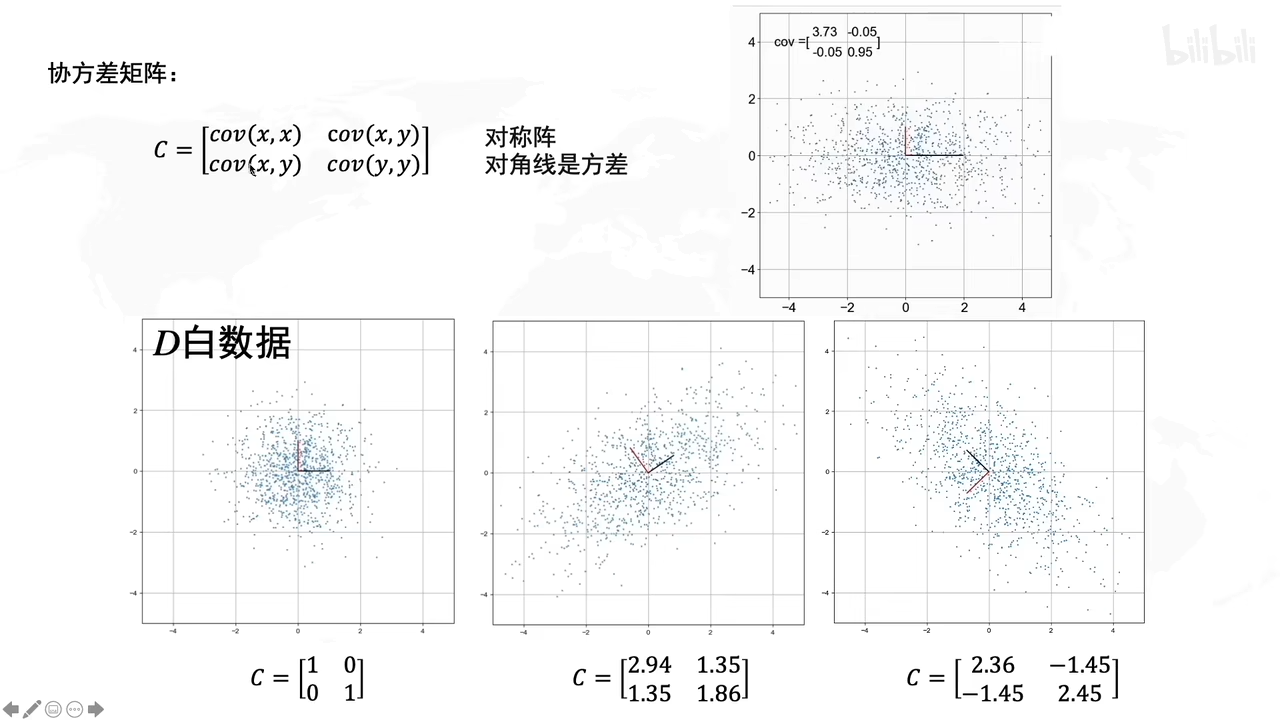
若x,y是不相关的话,那么cov(x,y)就是0
上图,
第一个小图就是x,y不相关
第二个小图就是x,y正相关(协方差大于0)
第二个小图就是x,y负相关(协方差小于0)

为什么是n-1?
(因为保证统计量的无偏性,保守估计比真实值偏大)
用白数据加上拉伸和旋转后,就得到D’
开始公示推导:(D’符合一般正态分布,可以标准化后与D一样的特性)
特征向量求解
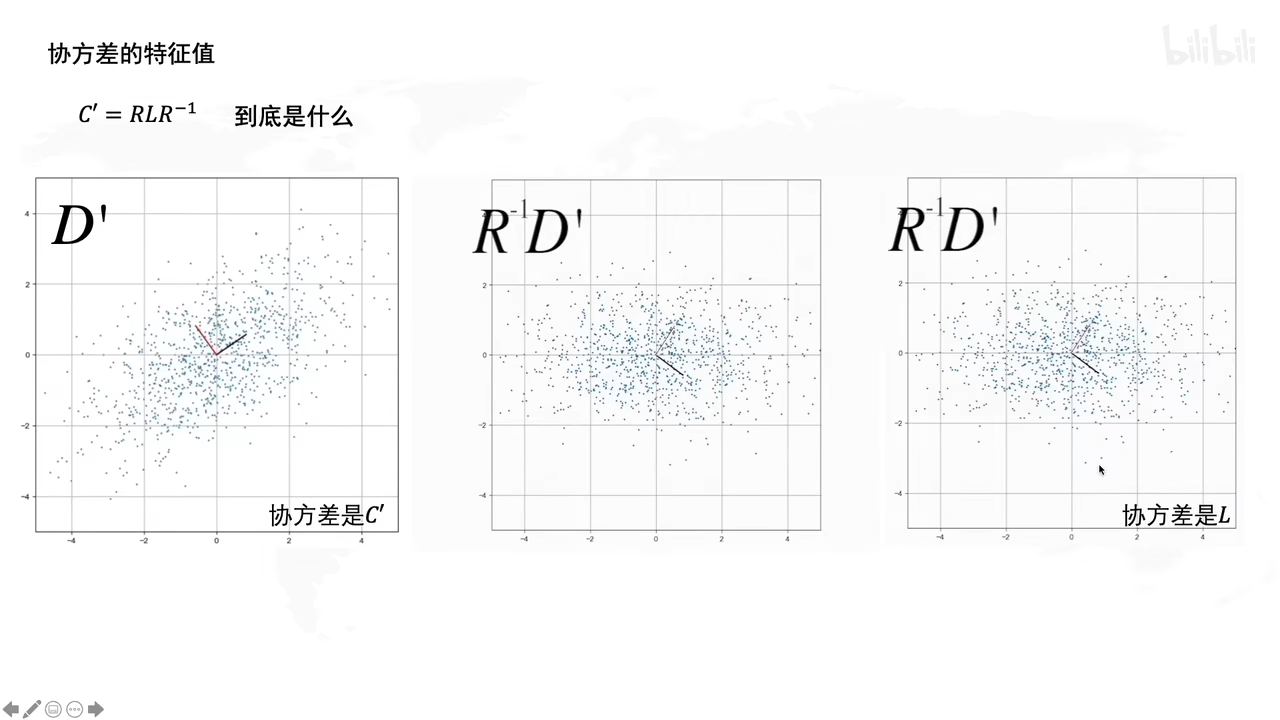
(听不懂了呜呜呜啊啊)
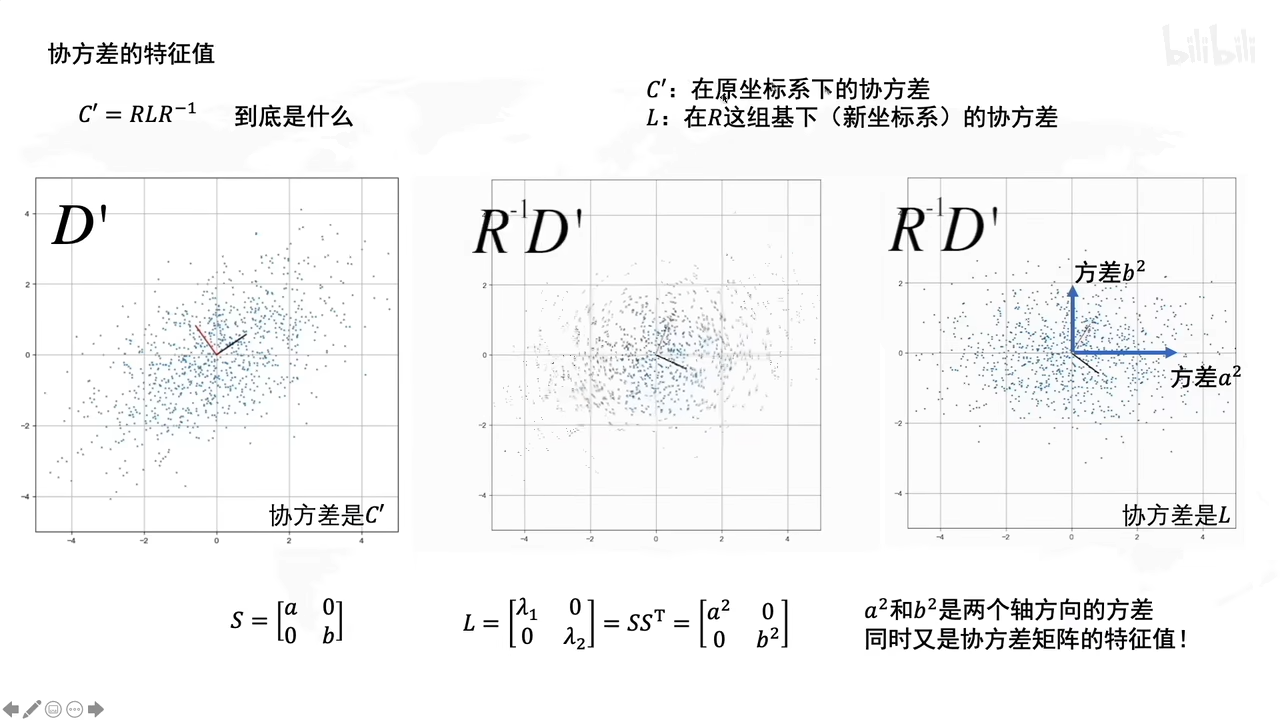
总结了:

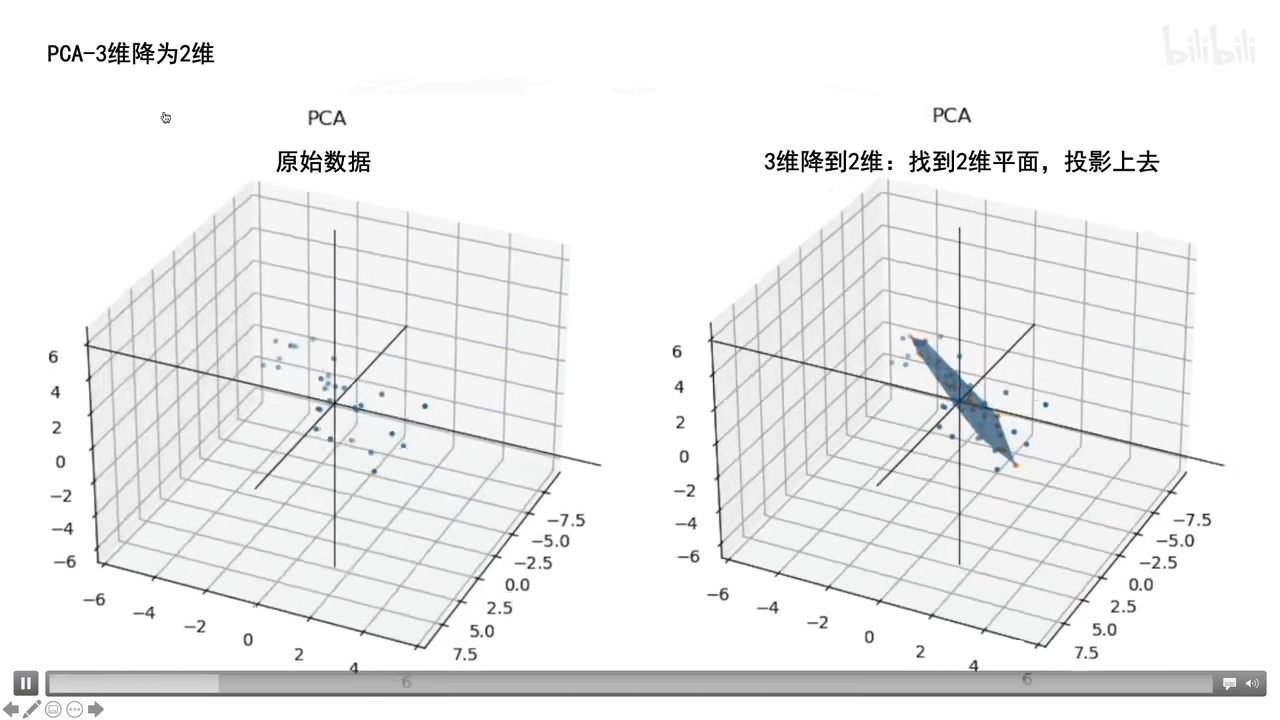
三维转二维就是找个二维平面然后投影,(让数据间方差最大的)
PCA和置信椭圆有什么关系?
(啥是置信椭圆???
置信椭圆基本上是对置信区域的描述方式,其长轴和短轴分别为置信区域的参数,置信椭圆的长短半轴,分别表示二维位置坐标分量的标准差(如经度的σλ和纬度的σφ)。
)
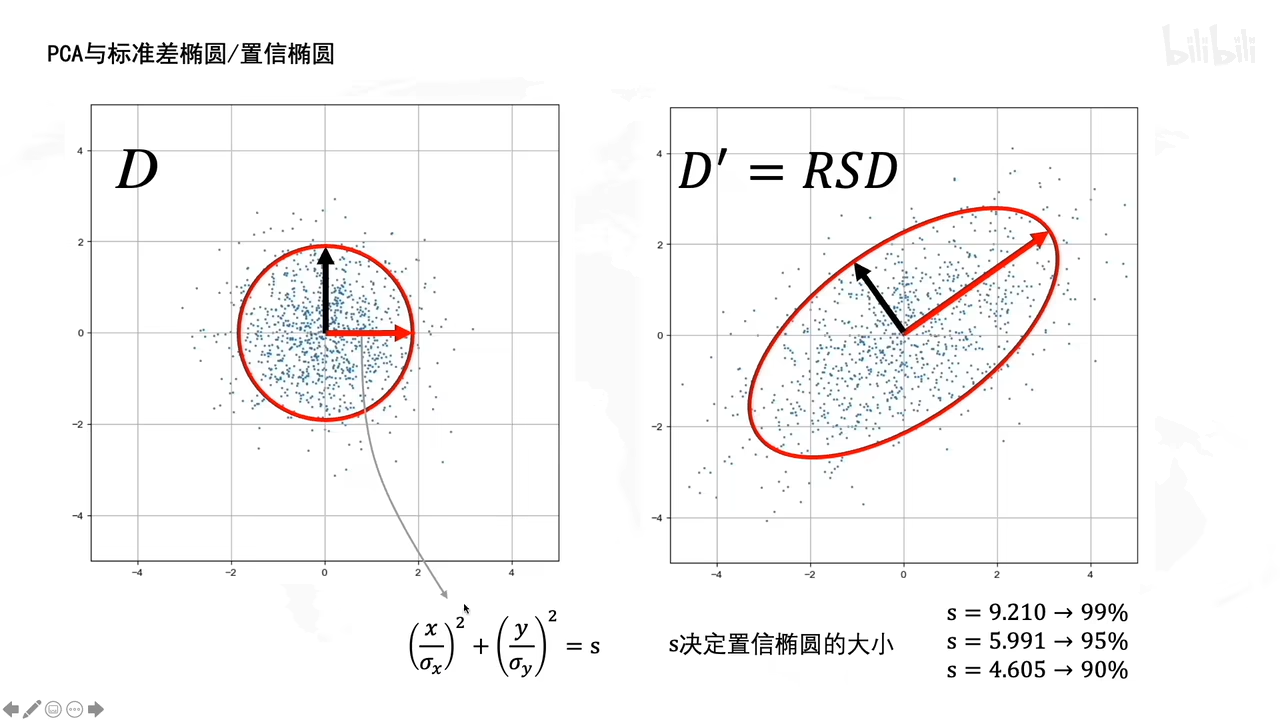
从白数据里面画了一个圆,(刚好有0.95的数据在圆内)拉伸旋转后成了一个圆,还是有0.95的数据点在椭圆里
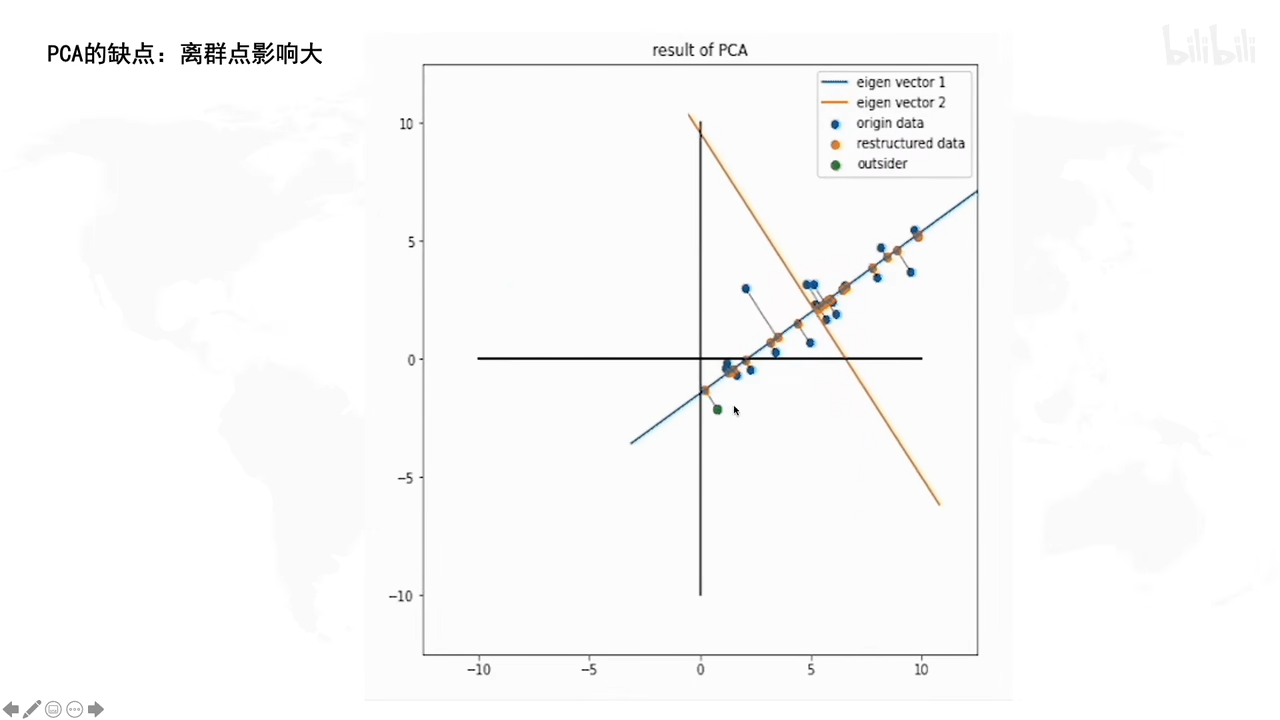
与奇异值分解的关系