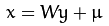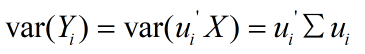首先，感谢一下这篇文章的作者：主成分分析原理及过程

PCA原理及过程

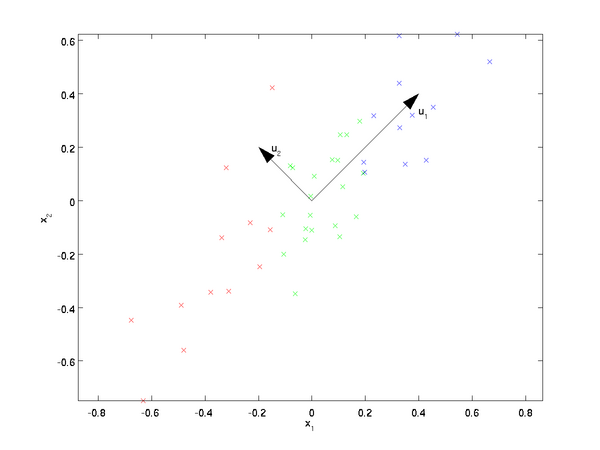
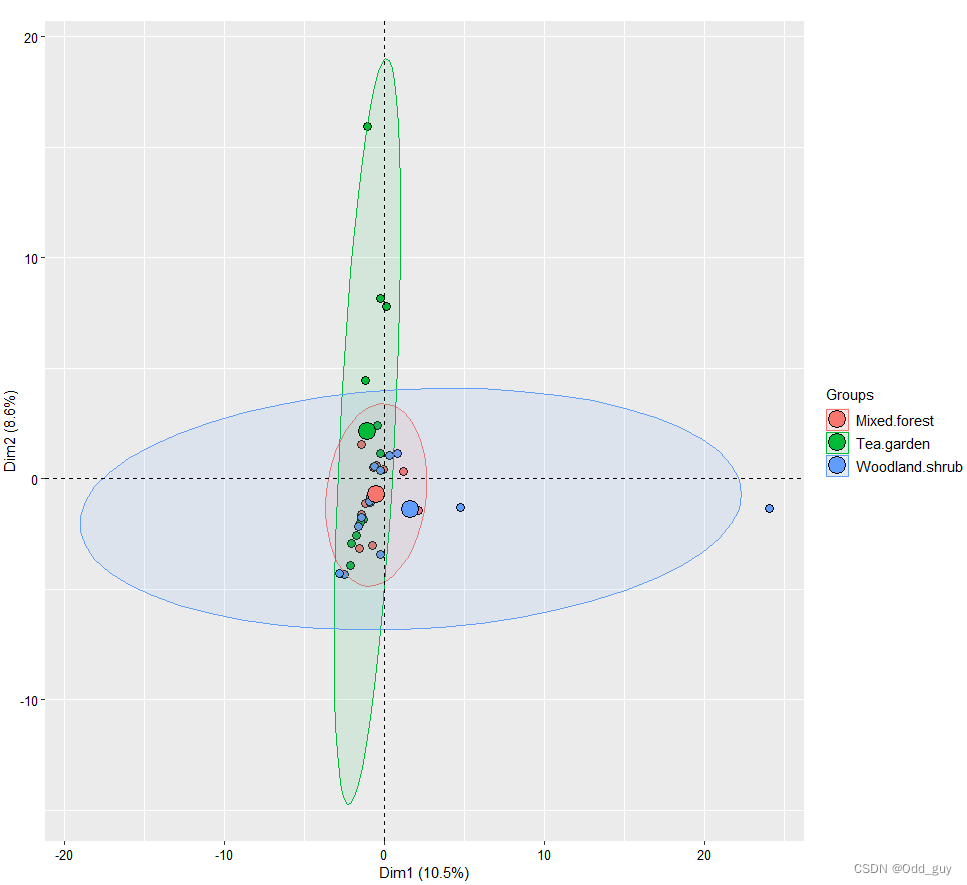
在机器学习中，对于数据维度过多问题，提出了一种降维算法叫做PCA算法。具体的降维：例如评估一个国家的GDP水平，需要考量到人口、收入、人均工资等等成千上万个因素。这每一个因素，我们叫做一个feature。如果feature过多，对于我们编写机器学习算法会有很大影响。而feature过多就是我们所说的维度灾难，为了解决这一问题，就提出了众多的降维算法，而今天所说的PCA只是其中一种。降维就是将原本过多的feature，映射到数量更少的feature组成的空间。当然了，映射也是随意映射就可以。需要按照一定的方法来进行数据的降维，下面就是PCA的主要过程：
在说算法流程之前需要知道协方差的概念，cov（X，Y）表示的意思就是X和Y的相关性，可以想象当cov（X，Y）为0时，就表示这两个X，Y之间不相关，对于我们的降维来说就是这两个维度要留下。
其次是样本的方差概念，方差表示的是维度的差异性大小，对于降维来说要选取差异大的，也就是方差大的。

• 协方差矩阵
  
  $$C_{i}j=cov(X_i,X_j)$$
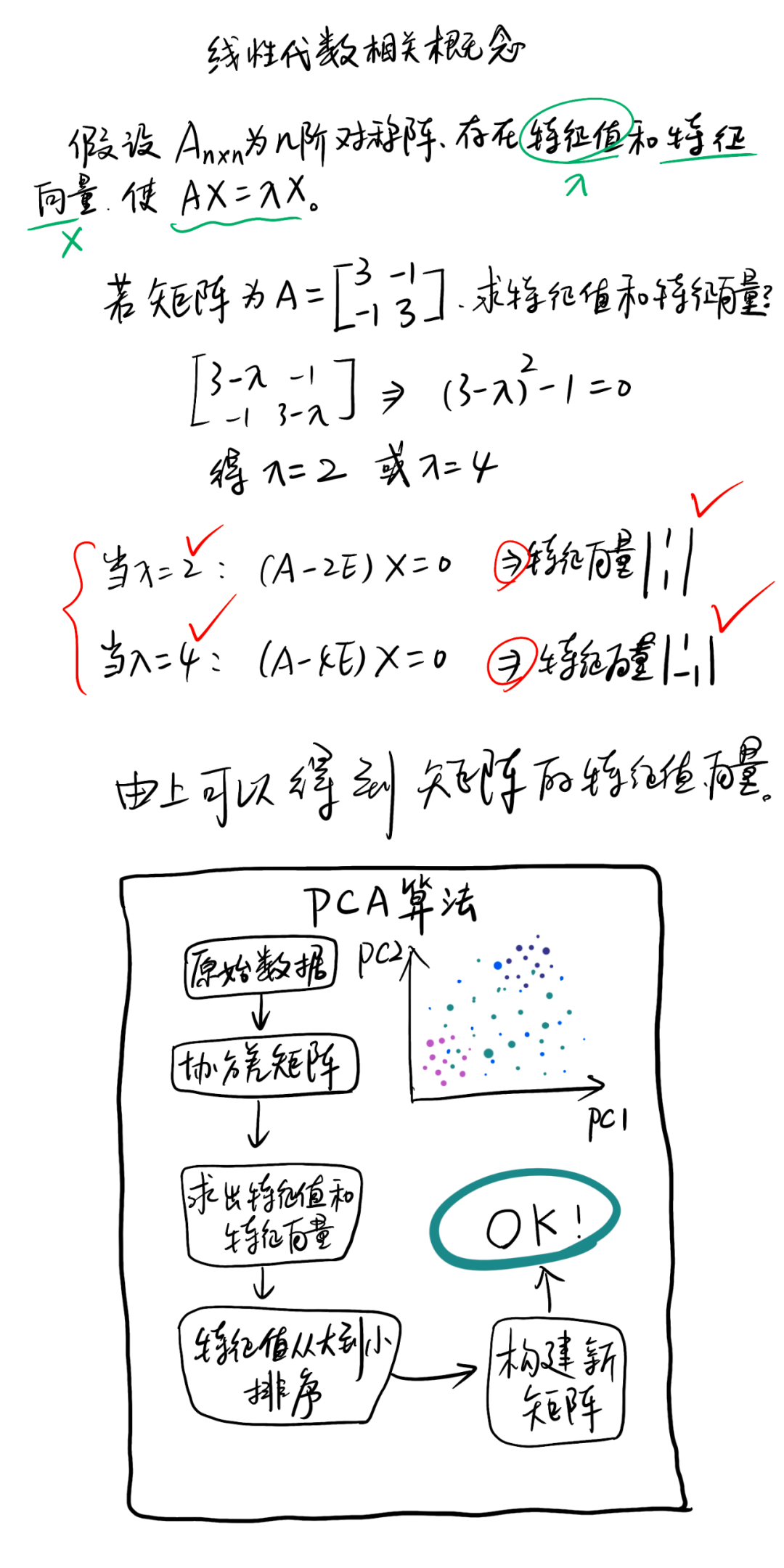
  首先求出来，上述的协方差矩阵。可以知道协方差矩阵对角线上的元素为对应维度的方差。
• 求其特征值和与其对应的特征向量
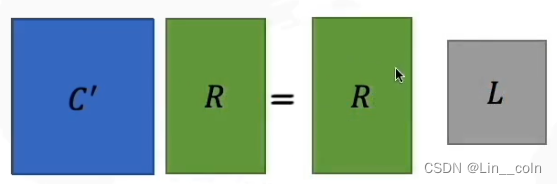
  我们需要使除了对角线之外的元素全为0，因此需要对协方差矩阵进行对角化操作，利用线性代数的知识求出该协方差矩阵的特征值和特征向量，对角化后，对角线上全为特征值，我们可以使用对角化后的对角矩阵和对应的特征向量对原数据进行操作。
• 选取前K个最大特征值对应的特征向量作为新的维度空间
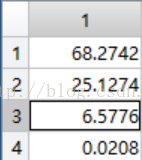
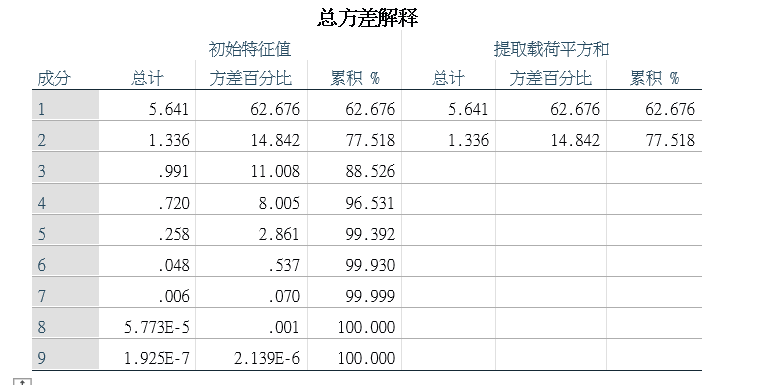
  对角化后的对角线上的元素就是协方差矩阵的特征值，同时这些值也表示这方差，因为要选取方差最大的，所以选取特征值大的K个对应的特征向量作为新的维度空间。
• 将原有数据映射到新的维度空间
  将原数据映射到新的维度空间，就是将原有数据与新选出的特征向量组成的矩阵相乘，得到原有数据在新的空间中每个维度上的投影分量。
  下面使用一个例子来演示一下映射过程：
  
  如上图，在XOY坐标系中有两个向量OA和OB且他们的模长都为1
  $$OA=(cos\theta ,sin\theta )andOB=(cos(\theta +\alpha ),sin(\theta +\alpha ))$$
  现将OA，OB转换到X’OY’坐标系中,新坐标轴的单位向量为：
  $$O{X}^{\prime }=(cos\theta ,sin\theta )andO{Y}^{\prime }=(-sin(\theta ),cos(\theta ))$$
  所以将原有的坐标与每一个新的坐标轴做内积即可得到该向量在新的坐标轴上的坐标，即：
  $$O{A}^{\prime }=(OA\ast O{X}^{\prime T},OA\ast O{Y}^{\prime T})=(1,0)$$
  $$O{B}^{\prime }=(OB\ast O{X}^{\prime T},OB\ast O{Y}^{\prime T})$$
  为了快速计算，通常写成矩阵的形式：
  $$\left[\begin{array}{c}O{A}^{\prime }\\ O{B}^{\prime }\end{array}\right]=\left[\begin{array}{c}OA\\ OB\end{array}\right]\left[\begin{array}{cc}O{X}^{\prime T}& O{Y}^{\prime T}\end{array}\right]$$