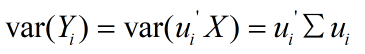主成分分析（Principal components analysis，以下简称PCA）是最重要的降维方法之一。在数据压缩消除冗余和数据噪音消除等领域都有广泛的应用。一般我们提到降维最容易想到的算法就是PCA，下面我们就对PCA的原理做一个总结。

1. PCA的思想

　　　　PCA顾名思义，就是找出数据里最主要的方面，用数据里最主要的方面来代替原始数据。具体的，假如我们的数据集是n维的，共有m个数据(x(1),x(2),...,x(m))(x(1),x(2),...,x(m))。我们希望将这m个数据的维度从n维降到n'维，希望这m个n'维的数据集尽可能的代表原始数据集。我们知道数据从n维降到n'维肯定会有损失，但是我们希望损失尽可能的小。那么如何让这n'维的数据尽可能表示原来的数据呢？

　　　　我们先看看最简单的情况，也就是n=2，n'=1,也就是将数据从二维降维到一维。数据如下图。我们希望找到某一个维度方向，它可以代表这两个维度的数据。图中列了两个向量方向，u1u1和u2u2，那么哪个向量可以更好的代表原始数据集呢？从直观上也可以看出，u1u1比u2u2好。

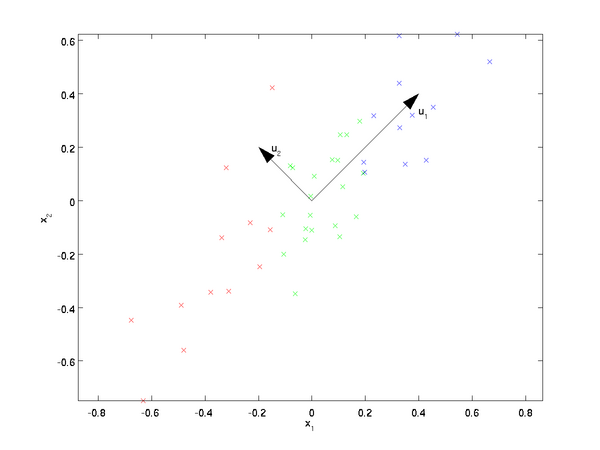
　　　　为什么u1u1比u2u2好呢？可以有两种解释，第一种解释是样本点到这个直线的距离足够近，第二种解释是样本点在这个直线上的投影能尽可能的分开。

　　　　假如我们把n'从1维推广到任意维，则我们的希望降维的标准为：样本点到这个超平面的距离足够近,或者说样本点在这个超平面上的投影能尽可能的分开。

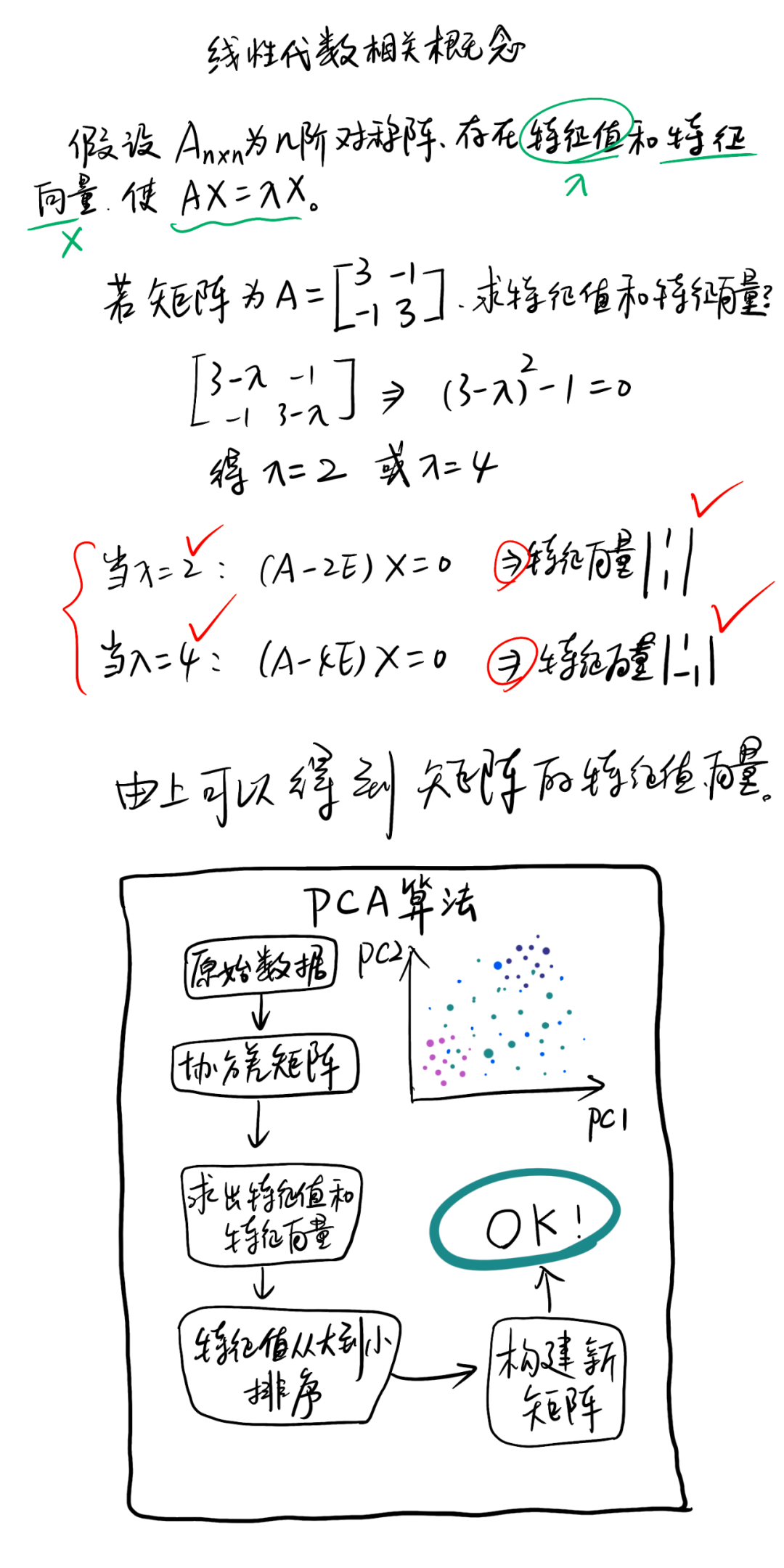
2. PCA算法总结

　　　　这里对PCA算法做一个总结。作为一个非监督学习的降维方法，它只需要特征值分解，就可以对数据进行压缩，去噪。因此在实际场景应用很广泛。为了克服PCA的一些缺点，出现了很多PCA的变种，比如第六节的为解决非线性降维的KPCA，还有解决内存限制的增量PCA方法Incremental PCA，以及解决稀疏数据降维的PCA方法Sparse PCA等。

　　　　PCA算法的主要优点有：

　　　　1）仅仅需要以方差衡量信息量，不受数据集以外的因素影响。　

　　　　2）各主成分之间正交，可消除原始数据成分间的相互影响的因素。

　　　　3）计算方法简单，主要运算是特征值分解，易于实现。

　　　　PCA算法的主要缺点有：

　　　　1）主成分各个特征维度的含义具有一定的模糊性，不如原始样本特征的解释性强。

　　　　2）方差小的非主成分也可能含有对样本差异的重要信息，因降维丢弃可能对后续数据处理有影响。

PCA算法具体原理请参考以下文章：

主成分分析（PCA）原理总结 - 刘建平Pinard - 博客园