矩阵的迹（Trace）

  $n\times n$的方阵A的n个对角线元素的和称为方阵A的迹，记作tr(A).

$A=\left(\begin{array}{ccc}{a}_{11}& \cdots & a_{1n}\\ ⋮& & ⋮\\ a_{n1}& \cdots & a_{nn}\end{array}\right)$
由定义知，$tr(A)=a_{11}+a_{22}+\cdots +a_{nn}=\sum _{j=0}^n{a}_{jj}$

矩阵的秩（Rank）

  定义1（比较晦涩）：域$F$上$n\times m$的非零矩阵A的所有子式中必有一个阶数最大的非零子式，其阶数称为矩阵A的秩，记作$rank(A)$. 零矩阵的秩定义为零。

  定义2：矩阵$A$的秩是$A$的列空间的维数，记作$rank(A)$。（因为$A$的主元列形成$A$的列空间$ColA$的一个基，所以$A$的秩正好是$A$的主元列的个数。）

  由于矩阵A的子式阶数不超过A的行数及列数，所以域$F$上$n\times m$的非零矩阵A的秩有：

（1）$0\le rank(A)\le min(n,m)$;
（2）$rank(cA)=rank(A)$，其中c为不等于0的常数；
（3）$rank(A^T)=rank(A)$;
（4）$rank(\overline{A})=rank(A)$, $rank(A^{\ast })=rank(A)$. 其中$\overline{A}$为$A$的共轭矩阵，$A^{\ast }$为$A$的伴随矩阵。

使用MATLAB求矩阵的秩(RANK)

  若要求矩阵$A$的秩，可以先将矩阵$A$化简为简化阶梯阵（reduced echelon form），然后数其主元列（pivot columns）数即为$A$的秩。

>>A = [1 2 3 4;4 5 6 7;6 9 12 15;1 1 1 1]
A =1              2              3              4       4              5              6              7       6              9             12             15       1              1              1              1  >>rref(A)   //求简化阶梯阵
ans =1              0             -1             -2       0              1              2              3       0              0              0              0       0              0              0              0 
//可见A的简化阶梯阵有2个主元列---第一列和第二列，所以秩为2. 可以使用rank()函数快速求矩阵的秩，进行验算>>rank(A)
ans =2     //验算结果和计算的主元列数一致。

  可见，对于上例的矩阵$A$，有两个主元列（第一和第二列），所以秩为2。由于上述矩阵化为简化阶梯阵后，有2列不是主元列，所以有方程$Ax=0$有2个自由变量（非主元列对应于方程$Ax=0$的自由变量），所以主元列加非主元列正好等于矩阵$A$的列数。所以可以得出一下秩定理：

秩定理：如果矩阵$A$有$n$列，那么$rankA+dimNulA=n$。

共轭矩阵（Conjugate Matrix）

  $n\times m$的复矩阵A的共轭矩阵是$m\times n$的矩阵（形如其转置矩阵），记作$A^{\ast }$：
$A=\left(\begin{array}{ccc}{a}_{11}& \cdots & a_{1m}\\ ⋮& & ⋮\\ a_{n1}& \cdots & a_{nm}\end{array}\right)$
$\overline{A}=\left(\begin{array}{ccc}\overline{a_{11}}& \cdots & \overline{a_{1m}}\\ ⋮& & ⋮\\ \overline{a_{n1}}& \cdots & \overline{a_{nm}}\end{array}\right)$
$A^{\ast }=\left(\begin{array}{ccc}\overline{a_{11}}& \cdots & \overline{a_{n1}}\\ ⋮& & ⋮\\ \overline{a_{1m}}& \cdots & \overline{a_{nm}}\end{array}\right)$

  共轭矩阵求法是，先将A转置，再对每个元素求共轭即可：
$$A^{\ast }=\overline{A^T}$$

  共轭矩阵也叫自共轭矩阵、Hermite矩阵，要求元素$a_{jk}$与$a_{kj}$共轭，即$\overline{a_{jk}}=\overline{a_{kj}}$如：
$\left(\begin{array}{cc}1& 3+2i\\ 3-2i& 1\end{array}\right)$中，$a_{12}=3+2i$与$a_{21}=3-2i$共轭相等，所以此矩阵为共轭矩阵。

伴随矩阵（Adjugate Matrix）

  设矩阵A为域F上的n阶方阵：
$$A=\left(\begin{array}{ccc}{a}_{11}& \cdots & a_{1n}\\ ⋮& & ⋮\\ a_{n1}& \cdots & a_{nn}\end{array}\right)$$
记$A_{jk}$为元素$a_{jk}$的代数余子式，用域F上$n^2$个数$A_{jk}$构成的n阶方阵即方阵A的伴随方阵，记作$A^{(\ast )}$。求法，先构成代数余子式矩阵：
$$\left(\begin{array}{cccc}{A}_{11}& A_{12}& \cdots & A_{1n}\\ A_{21}& A_{22}& ⋮& A_{2n}\\ ⋮& ⋮& & ⋮\\ A_{n1}& A_{n2}& \cdots & A_{nn}\end{array}\right)$$

再将其转置即可得到A的伴随矩阵$A^{(\ast )}$：

$$\left(\begin{array}{cccc}{A}_{11}& A_{21}& \cdots & A_{n1}\\ A_{12}& A_{22}& ⋮& A_{n2}\\ ⋮& ⋮& & ⋮\\ A_{1n}& A_{2n}& \cdots & A_{nn}\end{array}\right)$$

基底（Basis）维数（Dimension）与秩（Rank）

基底（或称基，basis）：如果向量空间$H$中的一组线性无关向量可以把该空间内所有向量通过线性组合的方式表示出来，那么这组向量成为该空间的一个基。
由定义知，基是一组向量的组合。

相对某个基的坐标的计算方法：如果 B = { b 1 , … , b p } B=\{b_1,\dots ,b_p\} B={b1​,…,bp​}是子空间$H$的一组基，对$H$中每一个向量$x$，相对于基 B = { b 1 , … , b p } B=\{b_1,\dots ,b_p\} B={b1​,…,bp​}的坐标是使得$x=c_1{b}_1+\cdots +c_p{b}_p$成立的权$c_1,\dots ,c_p$，且$R^p$中的向量$[x{]}_B=\left[\begin{array}{c}{c}_1\\ ⋮\\ c_p\end{array}\right]$称为$x$相对于基$B$的坐标向量，或称$x$的$B$-坐标向量。

例：设$v_1=\left[\begin{array}{c}3\\ 6\\ 2\end{array}\right]$，$v_2=\left[\begin{array}{c}-1\\ 0\\ 1\end{array}\right]$，$x=\left[\begin{array}{c}3\\ 12\\ 7\end{array}\right]$， B = { v 1 , v 2 } B=\{v_1,v_2\} B={v1​,v2​}，因为$v_1,v_2$显然线性无关，所以$B$是 H = S p a n { v 1 , v 2 } H=Span\{v_1,v_2\} H=Span{v1​,v2​}的基。请判断$x$是否在空间$H$中，如果在，请求出$x$相对于$B$的坐标向量。

解：

如果$x$在空间$H$中（空间$H$是v_1和v_2确定的平面），则方程$c_1{v}_1+c_2{v}_2=x$，$c_1$和$c_2$称为权，即：

$c_1\left[\begin{array}{c}3\\ 6\\ 2\end{array}\right]+c_2\left[\begin{array}{c}-1\\ 0\\ 1\end{array}\right]=\left[\begin{array}{c}3\\ 12\\ 7\end{array}\right]$是有解的（或说相容的）

如果权$c_1$、$c_2$存在，那么它们是$x$的$B$-坐标。

下面解方程：$c_1{v}_1+c_2{v}_2=x$对应的增广矩阵：

$\left[\begin{array}{ccc}3& -1& 3\\ 6& 0& 12\\ 2& 1& 7\end{array}\right]\to \left[\begin{array}{ccc}1& 0& 2\\ 0& 1& 3\\ 0& 0& 0\end{array}\right]$

即：$c=\left[\begin{array}{c}{c}_1\\ c_2\end{array}\right]=\left[\begin{array}{c}2\\ 3\end{array}\right]$

所以$[x{]}_B=\left[\begin{array}{c}{c}_1\\ c_2\end{array}\right]=\left[\begin{array}{c}2\\ 3\end{array}\right]$就是$x$相对于基$B$的坐标向量，或称$x$的$B$-坐标向量。

即：$x=2v_1+3v_2$，画图如下：

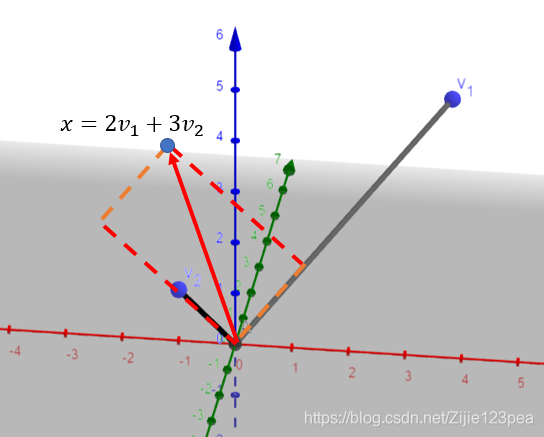
总结：

虽然$H$中的点也在$R^3$中，但是它们完全由属于$R^2$的坐标向量确定（因为本例中$H$是v_1和v_2确定的平面，属于$R^2$）。映射$x|\to [x{]}_B$是使$H$和$R^2$之间保持线性组合关系的一一映射，那么可以称这种映射是同构的，本例中$H$与$R^2$同构。

一般地，如果 B = { b 1 , … , b p } B=\{b_1,\dots ,b_p\} B={b1​,…,bp​}是子空间$H$的一组基，则映射$x|\to [x{]}_B$是使$H$和$R^p$的形态一样的一一映射（$H$中的向量可能多于$p$个元素）。