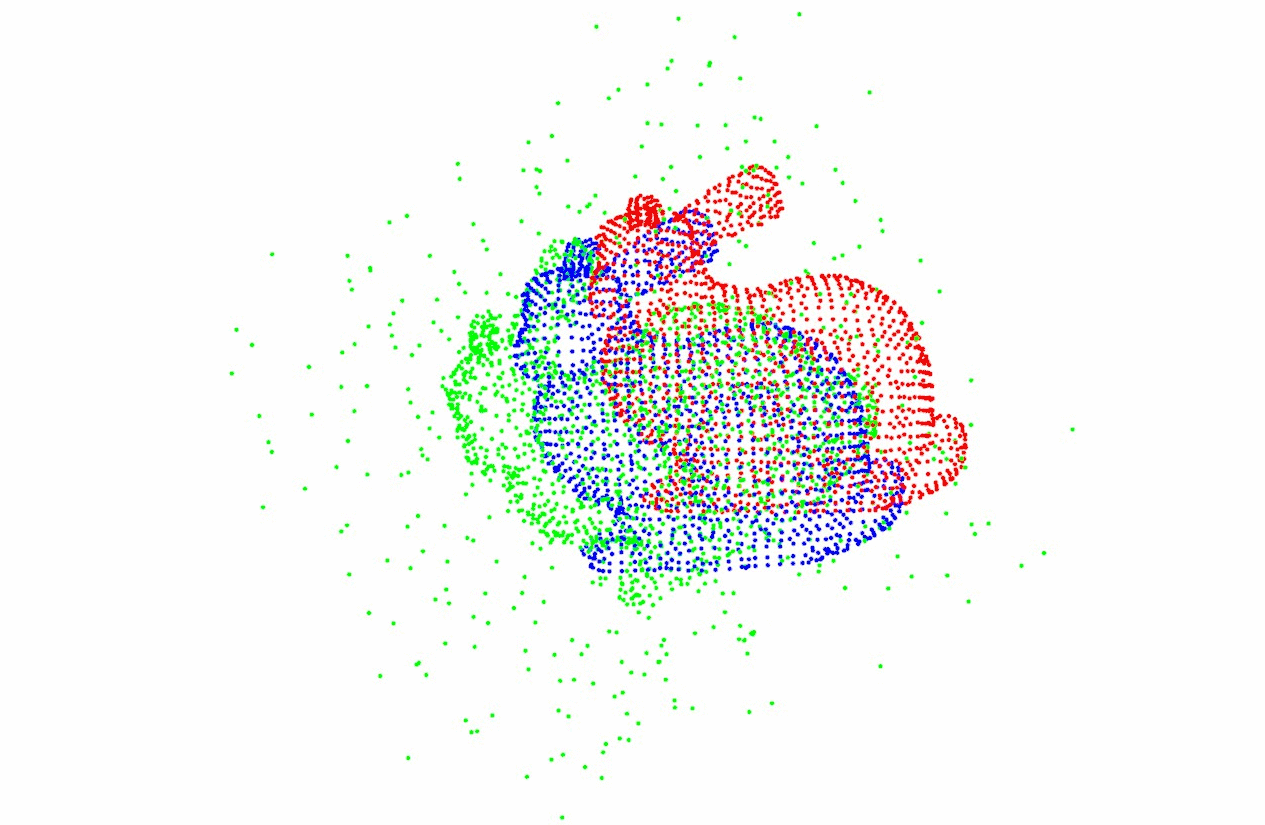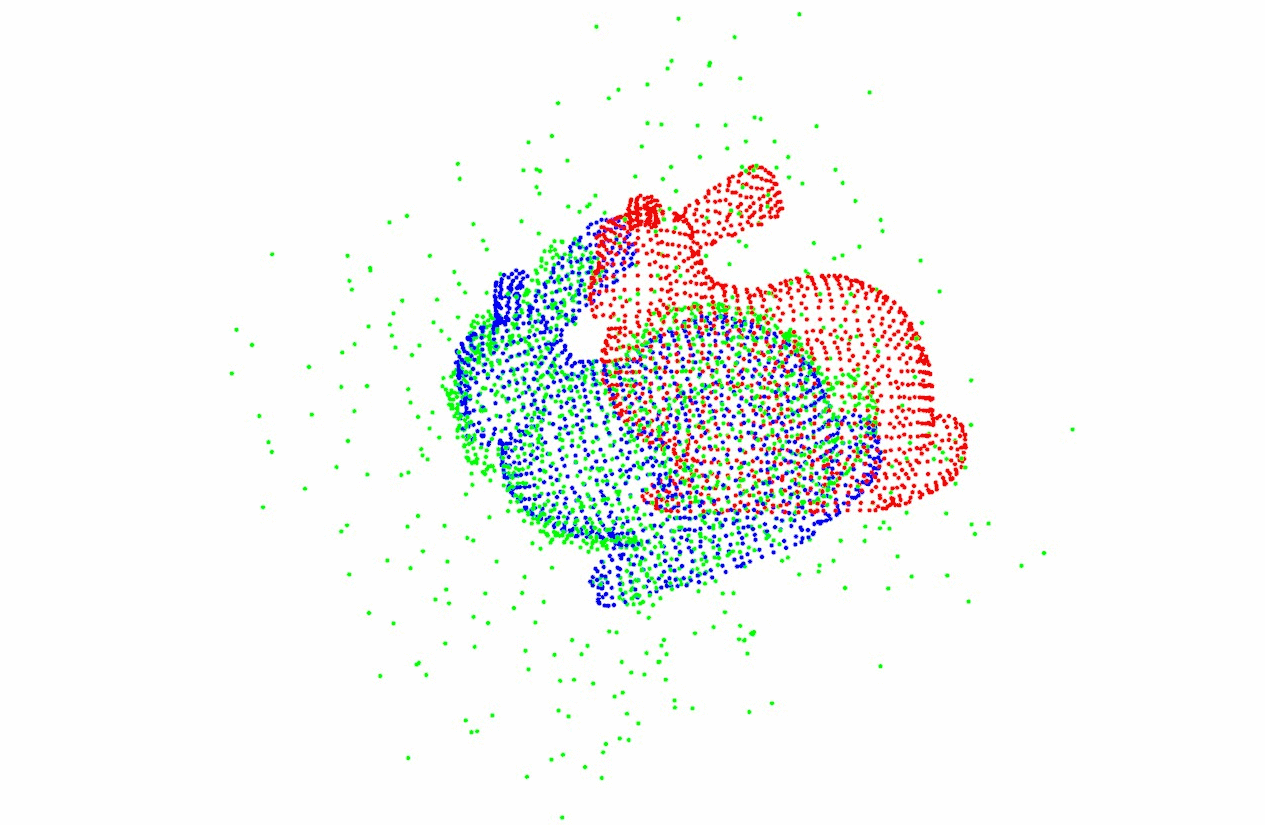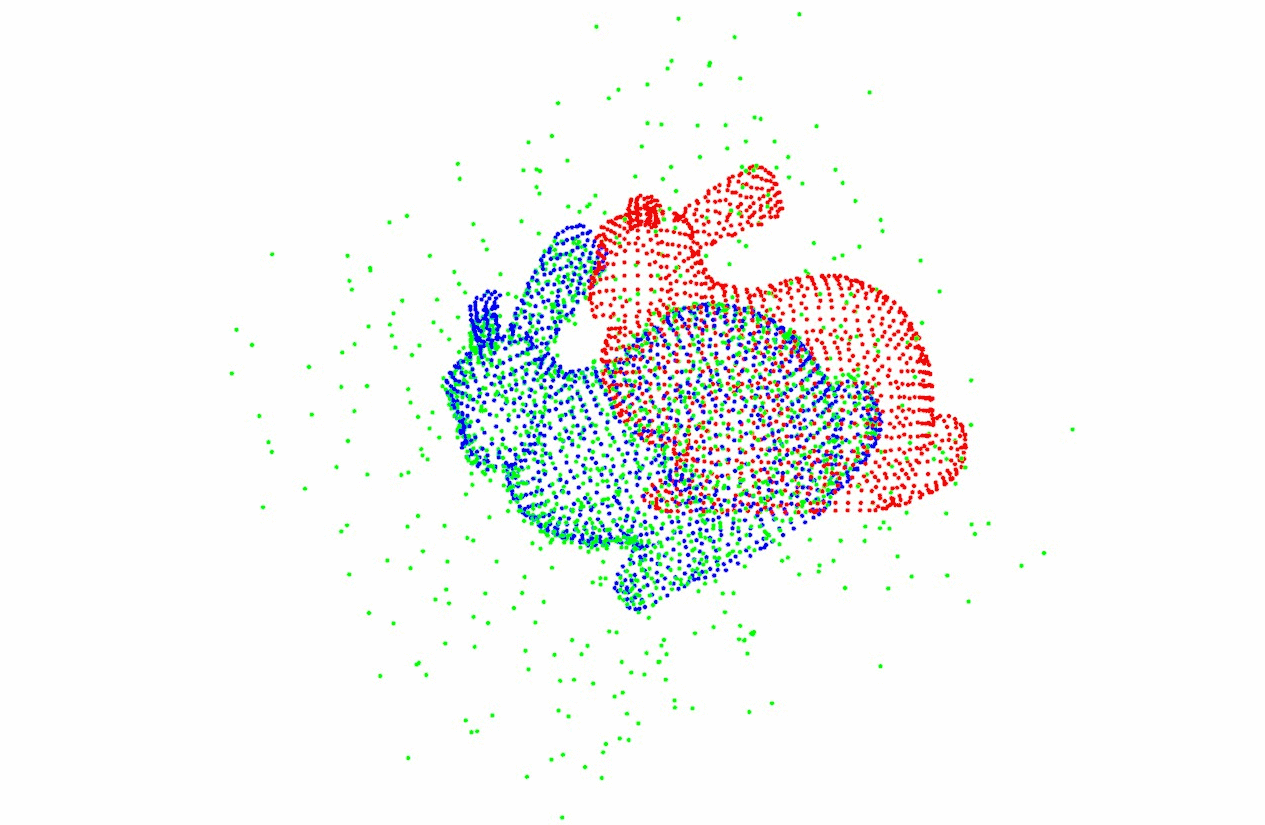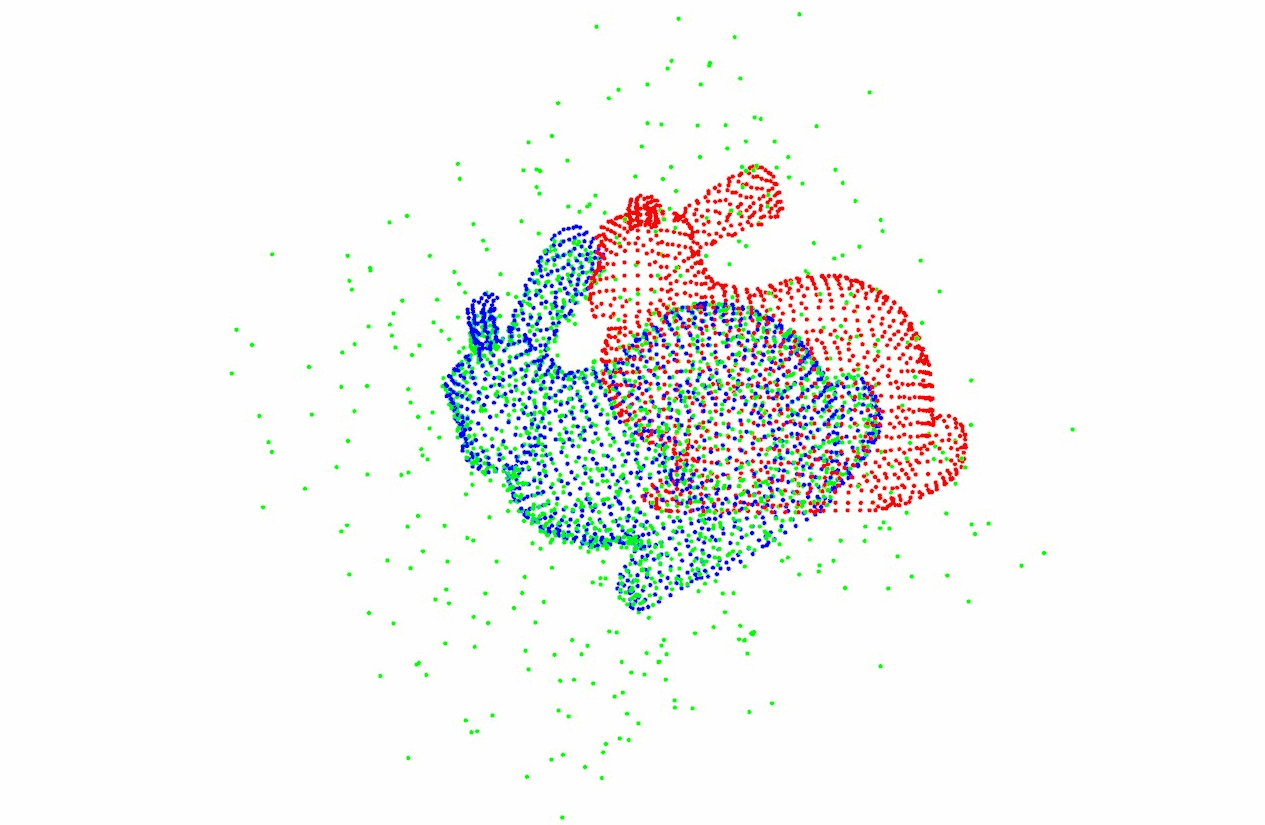
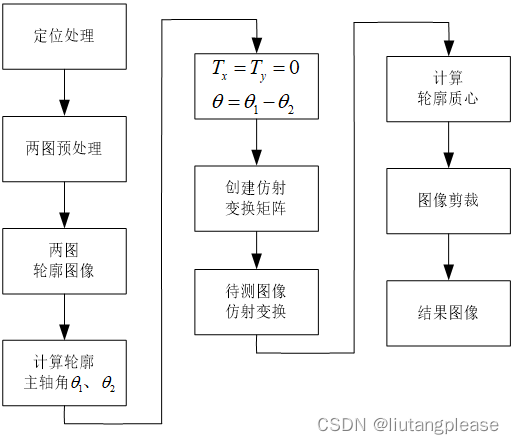
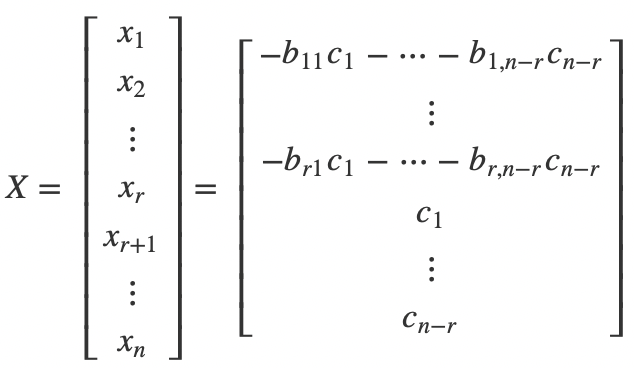二维ICP配准
- 1. 理论
- 1.1 ICP算法
- 1.2 目标函数
- 1.3 简化目标函数
- 1.4 变换矩阵求解
- 2. Python实现
- 2.1 导入模块
- 2.2. 定义相关函数
- 2.2.1 求解二维点间距函数
- 2.2.2 求解二维点距离点集最近点函数
- 2.2.3 求解二维点集间平均距离函数
- 2.3. 定义ICP_2D
- 2.4. 定义点云
- 2.5. ICP 配准
1. 理论
1.1 ICP算法
ICP算法本质上是基于最小二乘法的最优配准方法
重复进行选择对应关系点对, 计算最优刚体变换[R, T]
直到满足正确配准的收敛精度要求
即目的就是要找到待配准点云数据与参考云数据之间的旋转矩阵R和平移矩阵 T
使得两点数据之间满足某种度量准则下的最优匹配
1.2 目标函数
假设两帧点云A与B,将A 称为参考点云(也就是目标点云),把 B 称为源点云
在机器人定位的时候,A就为地图上的点云,B为设备感知的点云
如何定义两个点云匹配误差呢
一般定义所有最近点的欧式距离平方和为目标函数

平时要先去噪点,这里忽略
1.3 简化目标函数
上式存在两个变量,比较难处理
这时可通过归一化,就可先 不考虑平移矩阵 T

那么目标函数则为:

分解目标函数可得:

即使函数G最大即可

1.4 变换矩阵求解
现在取旋转矩阵R和平移矩阵 T

则函数G:

对函数G进行 theta 求极值,且令其为0,则有

只要求出:

就可以求出旋转角 theta
求出theta即可得到旋转矩阵R
再根据旋转矩阵R,求平移矩阵 T

然后不断迭代,至人为目标距离足够小即可
2. Python实现
2.1 导入模块
import numpy as np
import math# 不以科学计数显示
np.set_printoptions(suppress=True)
2.2. 定义相关函数
2.2.1 求解二维点间距函数
def GetDistOfPoints2D(p1, p2):'''求出两个点的距离'''return math.sqrt(math.pow(p2[0] - p1[0], 2) + math.pow(p2[1] - p1[1], 2))
2.2.2 求解二维点距离点集最近点函数
def GetClosestID(p, p_set):'''在p_set点集中找到距p最近点的id'''id = 0min = float("inf") # 初始化取最大值for i in range(p_set.shape[1]):dist = GetDistOfPoints2D(p, p_set[:, i])if dist < min:id = imin = distreturn id
2.2.3 求解二维点集间平均距离函数
def GetDistOf2DPointsSet(set1, set2):'''求两个点集之间的平均点距'''loss = 0for i in range(set1.shape[1]):id = GetClosestID(set1[:, i], set2)dist = GetDistOfPoints2D(set1[:, i], set2[:, id])loss += distreturn loss/set1.shape[1]
2.3. 定义ICP_2D
def ICP_2D(targetPoints, sourcePoints):'''二维 ICP 配准算法'''A = targetPoints # A是目标点云(地图值)B = sourcePoints # B是源点云(感知值)# 初始化迭代参数iteration_times = 0 # 迭代次数dist_now = 1 # A,B两点集之间初始化距离dist_improve = 1 # A,B两点集之间初始化距离提升dist_before = GetDistOf2DPointsSet(A, B) # A,B两点集之间距离# 初始化 R,TR = np.identity(2)T = np.zeros((2, 1))# 均一化点云A_mean = np.mean(A, axis=1).reshape((2, 1))A_ = A - A_mean# 迭代次数小于10并且距离大于0.01时,继续迭代while iteration_times < 10 and dist_now > 0.01:# 均一化点云B_mean = np.mean(B, axis=1).reshape((2, 1))B_ = B - B_mean# t_nume表示角度公式中的分子 t_deno表示分母t_nume, t_deno = 0, 0# 对源点云B中每个点进行循环for i in range(B_.shape[1]):j = GetClosestID(B_[:, i], A_) # 找到距离最近的目标点云A点idt_nume += A_[1][j] * B_[0][i] - A_[0][j] * B_[1][i] # 获得求和公式,分子的一项t_deno += A_[0][j] * B_[0][i] + A_[1][j] * B_[1][i] # 获得求和公式,分母的一项# 计算旋转弧度θtheta = math.atan2(t_nume, t_deno)# 由旋转弧度θ得到旋转矩阵Rdelta_R = np.array([[math.cos(theta), -math.sin(theta)], [math.sin(theta), math.cos(theta)]])# 计算平移矩阵Tdelta_T = A_mean - np.matmul(delta_R, B_mean)# 更新最新的点云B = np.matmul(delta_R, B) + delta_T# 更新旋转矩阵R和平移矩阵TR = np.matmul(delta_R, R)T = np.matmul(delta_R, T) + delta_T# 更新迭代iteration_times += 1 # 迭代次数+1dist_now = GetDistOf2DPointsSet(A, B) # 更新两个点云之间的距离dist_improve = dist_before - dist_now # 计算这一次迭代两个点云之间缩短的距离dist_before = dist_now # 将"现在距离"赋值给"以前距离"# 打印迭代次数、损失距离、损失提升print("迭代:第{}次,距离:{:.2f},缩短:{:.2f}".format(iteration_times, dist_now, dist_improve))return R, T
2.4. 定义点云
# 目标点云(地图上的数据)
a = np.array([[1, 2, 2], [1, 2, 3]])# 设置转换量
c_theta = math.radians(30) # 逆时针旋转30° 求解R旋转角度应为顺时针旋转30°
c_r = np.array([[math.cos(c_theta), -math.sin(c_theta)], [math.sin(c_theta), math.cos(c_theta)]])
c_t = np.array([[6], [-0.6]]) # 偏移(6,-0.6) 求解T应为(-6,0.6)# 源点云(假设检测到的数据)
b = np.matmul(c_r, a + c_t)# ICP 配准
r, t = ICP_2D(a, b)# 源点云(假设检测到的数据)
b = np.matmul(c_r, a + c_t)
2.5. ICP 配准
# ICP 配准
r, t = ICP_2D(a, b)# 显示参数
print("A:\n", a)
print("\nB:\n", b)
print("\nR:\n", r)
print("\nT:\n", t)
print("\nNew B:\n", np.matmul(r, b) + t)
input("\n输入任意键退出")# 迭代:第1次,距离:0.00,缩短:4.62
# A:
# [[1 2 2]
# [1 2 3]]# B:
# [[5.86217783 6.22820323 5.72820323]
# [3.84641016 5.21243557 6.07846097]]# R:
# [[ 0.8660254 0.5 ]
# [-0.5 0.8660254]]# T:
# [[-6. ]
# [ 0.6]]# New B:
# [[1. 2. 2.]
# [1. 2. 3.]]# 输入任意键退出
完整代码:
CSDN
Github
谢谢