原文链接：How to incrementally register pairs of cloudshttps://pcl.readthedocs.io/projects/tutorials/en/latest/pairwise_incremental_registration.html#pairwise-incremental-registration
https://pcl.readthedocs.io/projects/tutorials/en/latest/pairwise_incremental_registration.html#pairwise-incremental-registration
PCD文件：github.com/PointCloudLibrary/data/tree/master/tutorials/pairwise/https://github.com/PointCloudLibrary/data/tree/master/tutorials/pairwise
目录
程序代码
代码解析
头文件包含
全局变量
自定义数据解结构
自定义点云表示
加载多个PCD文件
整个程序结构
配准函数
输入参数
非线性ICP对象
手动迭代
实验结果
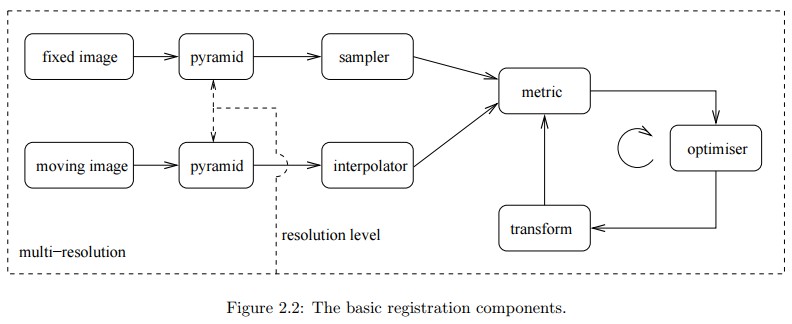
本教程演示了迭代最近点（ICP）算法的使用，以便逐步地对一系列点云进行两两匹配。它的思想是对所有的点云进行变换，使得都与第一个点云在统一的坐标系中。在每个连贯的有重叠的点云之间找到最佳的变换，并累积这些变换到全部的点云。能够进行ICP算法的点云需要粗略的预匹配，并且并且一个点云与另一个点云有重叠部分。
程序代码
/* \author Radu Bogdan Rusu* adaptation Raphael Favier*/
#include <boost/make_shared.hpp>//boost指针
#include <pcl/point_types.h>//点类型定义
#include <pcl/point_cloud.h>//点云类
#include <pcl/point_representation.h>//点表示
#include <pcl/io/pcd_io.h>//pcd输入输出操作
#include <pcl/filters/voxel_grid.h>//体素网格化滤波
#include <pcl/filters/filter.h>//滤波
#include <pcl/features/normal_3d.h>//法线特征
#include <pcl/registration/icp.h>//icp类
#include <pcl/registration/icp_nl.h> //非线性icp类
#include <pcl/registration/transforms.h>//变换矩阵类
#include <pcl/visualization/pcl_visualizer.h>//可视化类//颜色处理器
using pcl::visualization::PointCloudColorHandlerGenericField;
using pcl::visualization::PointCloudColorHandlerCustom;
//简单类型定义
typedef pcl::PointXYZ PointT;
typedef pcl::PointCloud<PointT> PointCloud;
typedef pcl::PointNormal PointNormalT; //法向量
typedef pcl::PointCloud<PointNormalT> PointCloudWithNormals;//带有法向量的点云//创建可视化工具
pcl::visualization::PCLVisualizer *p;
//定义左右视点
int vp_1, vp_2;
//处理点云的方便的结构定义
struct PCD
{PointCloud::Ptr cloud;//点云指针std::string f_name;//文件名PCD() : cloud(new PointCloud) {};
};
struct PCDComparator
{bool operator () (const PCD& p1, const PCD& p2){return (p1.f_name < p2.f_name);//文件名是否相同}
};
//以< x, y, z, curvature >形式定义一个新的点，表示x,y,z+曲率
class MyPointRepresentation : public pcl::PointRepresentation <PointNormalT>
{using pcl::PointRepresentation<PointNormalT>::nr_dimensions_;//维度
public:MyPointRepresentation(){//定义尺寸值nr_dimensions_ = 4;}//覆盖copyToFloatArray方法来定义我们的特征矢量virtual void copyToFloatArray(const PointNormalT &p, float * out) const{// < x, y, z, curvature >out[0] = p.x;out[1] = p.y;out[2] = p.z;out[3] = p.curvature;//曲率}
};/** 在可视化窗口的第一视点显示源点云和目标点云* 左视图用来显示未匹配的源点云和目标点云* 红色代表源点云,绿色代表目标点云*/
void showCloudsLeft(const PointCloud::Ptr cloud_target, const PointCloud::Ptr cloud_source)
{p->removePointCloud("vp1_target");p->removePointCloud("vp1_source");PointCloudColorHandlerCustom<PointT> tgt_h(cloud_target, 0, 255, 0);//greenPointCloudColorHandlerCustom<PointT> src_h(cloud_source, 255, 0, 0);//redp->addPointCloud(cloud_target, tgt_h, "vp1_target", vp_1);p->addPointCloud(cloud_source, src_h, "vp1_source", vp_1);PCL_INFO("Press q to begin the registration.\n");p->spin();
}/**在可视化窗口的第二视点显示源点云和目标点云* 右边显示配准后的源点云和目标点云*/
void showCloudsRight(const PointCloudWithNormals::Ptr cloud_target, const PointCloudWithNormals::Ptr cloud_source)
{p->removePointCloud("source");p->removePointCloud("target");// 以曲率字段来控制点云颜色的显示PointCloudColorHandlerGenericField<PointNormalT> tgt_color_handler(cloud_target, "curvature");if (!tgt_color_handler.isCapable())PCL_WARN("Cannot create curvature color handler!");PointCloudColorHandlerGenericField<PointNormalT> src_color_handler(cloud_source, "curvature");if (!src_color_handler.isCapable())PCL_WARN("Cannot create curvature color handler!");p->addPointCloud(cloud_target, tgt_color_handler, "target", vp_2);p->addPointCloud(cloud_source, src_color_handler, "source", vp_2);p->spinOnce();
}/**加载一组我们想要匹配在一起的PCD文件* 参数argc是参数的数量 (pass from main ())*参数 argv 实际的命令行参数 (pass from main ())*参数models点云数据集的合成矢量*/
void loadData(int argc, char **argv, std::vector<PCD, Eigen::aligned_allocator<PCD> > &models)
{std::string extension(".pcd");//假定第一个参数是实际测试模型for (int i = 1; i < argc; i++){std::string fname = std::string(argv[i]);// 至少需要5个字符长（因为.pcd就有4个字符）if (fname.size() <= extension.size())continue;std::transform(fname.begin(), fname.end(), fname.begin(), (int(*)(int))tolower);//检查参数是一个pcd文件if (fname.compare(fname.size() - extension.size(), extension.size(), extension) == 0){//加载点云并保存在总体的模型列表中PCD m;m.f_name = argv[i];pcl::io::loadPCDFile(argv[i], *m.cloud);//从点云中移除NAN点std::vector<int> indices;pcl::removeNaNFromPointCloud(*m.cloud, *m.cloud, indices);models.push_back(m);}}
}/**匹配一对点云数据集并且返还结果*参数 cloud_src 是源点云*参数 cloud_tgt 是目标点云*参数 output 输出的配准结果的源点云*参数 final_transform 是在来源和目标之间的转换*参数 downsample 是否需要进行下采样*/
void pairAlign(const PointCloud::Ptr cloud_src, const PointCloud::Ptr cloud_tgt, PointCloud::Ptr output, Eigen::Matrix4f &final_transform, bool downsample = false)
{//为了一致性和高速的下采样//注意：为了大数据集需要允许这项PointCloud::Ptr src(new PointCloud);PointCloud::Ptr tgt(new PointCloud);pcl::VoxelGrid<PointT> grid;//体素滤波// 是否先对点云进行下采样if (downsample){grid.setLeafSize(0.05, 0.05, 0.05);grid.setInputCloud(cloud_src);grid.filter(*src);grid.setInputCloud(cloud_tgt);grid.filter(*tgt);}else{src = cloud_src;tgt = cloud_tgt;}//计算曲面法线和曲率PointCloudWithNormals::Ptr points_with_normals_src(new PointCloudWithNormals);PointCloudWithNormals::Ptr points_with_normals_tgt(new PointCloudWithNormals);pcl::NormalEstimation<PointT, PointNormalT> norm_est;//点云法线估计对象// 使用KD树进行搜索//添加搜索算法 kdtree search 最近的几个点 估计平面 协方差矩阵PCA分解 求解法线pcl::search::KdTree<pcl::PointXYZ>::Ptr tree(new pcl::search::KdTree<pcl::PointXYZ>());norm_est.setSearchMethod(tree);norm_est.setKSearch(30); //设置最近邻居的数量k，k最近邻搜索norm_est.setInputCloud(src);norm_est.compute(*points_with_normals_src);//计算表面法线特征并保存结果pcl::copyPointCloud(*src, *points_with_normals_src);//不同类型的点云之间的转换norm_est.setInputCloud(tgt);norm_est.compute(*points_with_normals_tgt);pcl::copyPointCloud(*tgt, *points_with_normals_tgt);//举例说明我们自定义点的表示（以上定义）MyPointRepresentation point_representation;//调整'curvature'尺寸权重以便使它和x, y, z平衡float alpha[4] = { 1.0, 1.0, 1.0, 1.0 };point_representation.setRescaleValues(alpha);// 配准//IterativeClosestPointNonLinear是一个ICP变体，使用Levenberg-Marquardt优化后端。合成的转换矩阵被优化为四元数。pcl::IterativeClosestPointNonLinear<PointNormalT, PointNormalT> reg;reg.setTransformationEpsilon(1e-6);//设置收敛判断条件，数值越小则精度越大，收敛也越慢//将两个对应关系之间的(src<->tgt)最大距离设置为10厘米//注意：根据你的数据集大小来调整reg.setMaxCorrespondenceDistance(0.1);//大于10cm的点不考虑//设置点表示reg.setPointRepresentation(boost::make_shared<const MyPointRepresentation>(point_representation));reg.setInputCloud(points_with_normals_src);//原点云reg.setInputTarget(points_with_normals_tgt);//目标点云////在一个循环中运行相同的最优化并且使结果可视化Eigen::Matrix4f Ti = Eigen::Matrix4f::Identity(), prev, targetToSource;PointCloudWithNormals::Ptr reg_result = points_with_normals_src;reg.setMaximumIterations(2);//最大迭代次数，每次迭代两次就认为收敛//手动迭代，每手动迭代一次，在窗口对最新的迭代结果进行刷新显示for (int i = 0; i < 30; ++i){PCL_INFO("Iteration Nr. %d.\n", i);//为了可视化的目的保存点云points_with_normals_src = reg_result;//估计reg.setInputCloud(points_with_normals_src);// 开始配准，并将结果保存在reg_resultreg.align(*reg_result);//在每一个迭代之间累积转换Ti = reg.getFinalTransformation() * Ti;//如果这次转换和之前转换之间的差异小于阈值//则通过减小最大对应距离来改善程序if (fabs((reg.getLastIncrementalTransformation() - prev).sum()) < reg.getTransformationEpsilon())reg.setMaxCorrespondenceDistance(reg.getMaxCorrespondenceDistance() - 0.001);prev = reg.getLastIncrementalTransformation();//可视化当前状态showCloudsRight(points_with_normals_tgt, points_with_normals_src);}//// 得到目标点云到源点云的变换targetToSource = Ti.inverse();////把目标点云转换回源框架pcl::transformPointCloud(*cloud_tgt, *output, targetToSource);p->removePointCloud("source");p->removePointCloud("target");PointCloudColorHandlerCustom<PointT> cloud_tgt_h(output, 0, 255, 0);//配准后的点云为红色PointCloudColorHandlerCustom<PointT> cloud_src_h(cloud_src, 255, 0, 0);//原始点云为绿色p->addPointCloud(output, cloud_tgt_h, "target", vp_2);p->addPointCloud(cloud_src, cloud_src_h, "source", vp_2);PCL_INFO("Press q to continue the registration.\n");p->spin();p->removePointCloud("source");p->removePointCloud("target");//添加源点云到转换目标*output += *cloud_src;final_transform = targetToSource;
}
/* ---[ */
int main(int argc, char** argv)
{// 加载数据std::vector<PCD, Eigen::aligned_allocator<PCD> > data;loadData(argc, argv, data);//检查用户输入if (data.empty()){PCL_ERROR("Syntax is: %s <source.pcd> <target.pcd> [*]\n", argv[0]);PCL_ERROR("[*] - multiple files can be added. The registration results of (i, i+1) will be registered against (i+2), etc\n");PCL_INFO("Example: %s `rospack find pcl`/test/bun0.pcd `rospack find pcl`/test/bun4.pcd\n", argv[0]);return (-1);}PCL_INFO("Loaded %d datasets.", (int)data.size());//创建一个PCL可视化对象p = new pcl::visualization::PCLVisualizer(argc, argv, "Pairwise Incremental Registration example");p->createViewPort(0.0, 0, 0.5, 1.0, vp_1);p->createViewPort(0.5, 0, 1.0, 1.0, vp_2);PointCloud::Ptr result(new PointCloud), source, target;Eigen::Matrix4f GlobalTransform = Eigen::Matrix4f::Identity(), pairTransform;//循环处理所有点云for (size_t i = 1; i < data.size(); ++i){source = data[i - 1].cloud;//连续配准target = data[i].cloud;//相邻两组点云//添加可视化数据showCloudsLeft(source, target);PointCloud::Ptr temp(new PointCloud);PCL_INFO("Aligning %s (%d) with %s (%d).\n", data[i - 1].f_name.c_str(), source->points.size(), data[i].f_name.c_str(), target->points.size());//pairTransform返回从目标点云target到source的变换矩阵pairAlign(source, target, temp, pairTransform, true);//把当前两两配准后的点云temp转化到全局坐标系下返回resultpcl::transformPointCloud(*temp, *result, GlobalTransform);//用当前的两组点云之间的变换更新全局变换std::cout << "GlobalTransform:" << std::endl;std::cout << GlobalTransform << std::endl;GlobalTransform = pairTransform * GlobalTransform;//保存配准对，转换到第一个点云框架中std::stringstream ss;ss << i << ".pcd";pcl::io::savePCDFile(ss.str(), *result, true);}
}
/* ]--- */
代码解析
头文件包含
#include <boost/make_shared.hpp>//boost指针
#include <pcl/point_types.h>//点类型定义
#include <pcl/point_cloud.h>//点云类
#include <pcl/point_representation.h>//点表示
#include <pcl/io/pcd_io.h>//pcd输入输出操作
#include <pcl/filters/voxel_grid.h>//体素网格化滤波
#include <pcl/filters/filter.h>//滤波
#include <pcl/features/normal_3d.h>//法线特征
#include <pcl/registration/icp.h>//icp类
#include <pcl/registration/icp_nl.h> //非线性icp类
#include <pcl/registration/transforms.h>//变换矩阵类
#include <pcl/visualization/pcl_visualizer.h>//可视化类全局变量
为了可视化目的，方便用户直观地观察到配准前后结果以及配准过程 ，创建全局可视化对象变量，并定义左右视点分别显示配准前和配准后的结果点云。
//创建可视化工具
pcl::visualization::PCLVisualizer *p;
//定义左右视点
int vp_1, vp_2;自定义数据解结构
声明一个结构体，方便对点云以文件名和点云对象进行成对处理管理，在配准过程中，可以接受多个点云文件输入，程序从第一个文件开始，连续的两两配准处理，然后存储配准后的点云文件。
//处理点云的方便的结构定义
struct PCD
{PointCloud::Ptr cloud;//点云指针std::string f_name;//文件名PCD() : cloud(new PointCloud) {};
};
struct PCDComparator
{bool operator () (const PCD& p1, const PCD& p2){return (p1.f_name < p2.f_name);//文件名是否相同}
};自定义点云表示
详细介绍参考：Adding your own custom PointT type
//以< x, y, z, curvature >形式定义一个新的点，表示x,y,z+曲率
class MyPointRepresentation : public pcl::PointRepresentation <PointNormalT>
{using pcl::PointRepresentation<PointNormalT>::nr_dimensions_;//维度
public:MyPointRepresentation(){//定义尺寸值nr_dimensions_ = 4;}//覆盖copyToFloatArray方法来定义我们的特征矢量virtual void copyToFloatArray(const PointNormalT &p, float * out) const{// < x, y, z, curvature >out[0] = p.x;out[1] = p.y;out[2] = p.z;out[3] = p.curvature;//曲率}
};加载多个PCD文件
/**加载一组我们想要匹配在一起的PCD文件* 参数argc是参数的数量 (pass from main ())*参数 argv 实际的命令行参数 (pass from main ())*参数models点云数据集的合成矢量*/
void loadData(int argc, char **argv, std::vector<PCD, Eigen::aligned_allocator<PCD> > &models)
{std::string extension(".pcd");//假定第一个参数是实际测试模型for (int i = 1; i < argc; i++){std::string fname = std::string(argv[i]);// 至少需要5个字符长（因为.pcd就有4个字符）if (fname.size() <= extension.size())continue;std::transform(fname.begin(), fname.end(), fname.begin(), (int(*)(int))tolower);//检查参数是一个pcd文件if (fname.compare(fname.size() - extension.size(), extension.size(), extension) == 0){//加载点云并保存在总体的模型列表中PCD m;m.f_name = argv[i];pcl::io::loadPCDFile(argv[i], *m.cloud);//从点云中移除NAN点std::vector<int> indices;pcl::removeNaNFromPointCloud(*m.cloud, *m.cloud, indices);models.push_back(m);}}
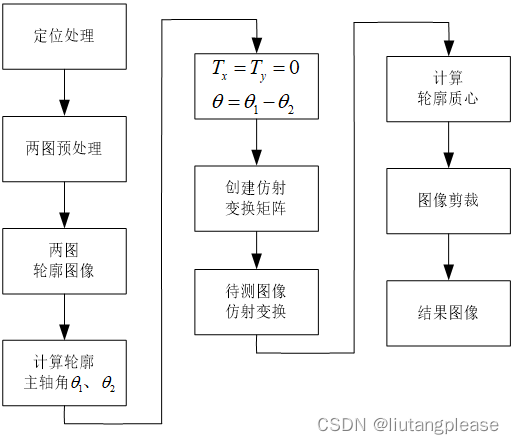
}整个程序结构
- 主函数检查用户输入，在点云列表中加载了用户输入的所有点云数据
- 建立两个视口的可视化对象：左边显示未配准的源点云和目标点云，右边显示配准后的源和目标点云。
- 在为一对点云找到变换矩阵后，将目标点云变换到源点云坐标系下，
- 将源点云和变换后的目标点云存储到同一点云文件。
- 利用此次找到的变换矩阵更新全局变换，用于将后续的点云都变换到与第一个输入点云相同坐标系下。
int main(int argc, char** argv)
{// 加载数据std::vector<PCD, Eigen::aligned_allocator<PCD> > data;loadData(argc, argv, data);//检查用户输入if (data.empty()){PCL_ERROR("Syntax is: %s <source.pcd> <target.pcd> [*]\n", argv[0]);PCL_ERROR("[*] - multiple files can be added. The registration results of (i, i+1) will be registered against (i+2), etc\n");PCL_INFO("Example: %s `rospack find pcl`/test/bun0.pcd `rospack find pcl`/test/bun4.pcd\n", argv[0]);return (-1);}PCL_INFO("Loaded %d datasets.", (int)data.size());//创建一个PCL可视化对象p = new pcl::visualization::PCLVisualizer(argc, argv, "Pairwise Incremental Registration example");p->createViewPort(0.0, 0, 0.5, 1.0, vp_1);p->createViewPort(0.5, 0, 1.0, 1.0, vp_2);PointCloud::Ptr result(new PointCloud), source, target;Eigen::Matrix4f GlobalTransform = Eigen::Matrix4f::Identity(), pairTransform;//循环处理所有点云for (size_t i = 1; i < data.size(); ++i){source = data[i - 1].cloud;//连续配准target = data[i].cloud;//相邻两组点云//添加可视化数据showCloudsLeft(source, target);PointCloud::Ptr temp(new PointCloud);PCL_INFO("Aligning %s (%d) with %s (%d).\n", data[i - 1].f_name.c_str(), source->points.size(), data[i].f_name.c_str(), target->points.size());//pairTransform返回从目标点云target到source的变换矩阵pairAlign(source, target, temp, pairTransform, true);//把当前两两配准后的点云temp转化到全局坐标系下返回resultpcl::transformPointCloud(*temp, *result, GlobalTransform);//用当前的两组点云之间的变换更新全局变换std::cout << "GlobalTransform:" << std::endl;std::cout << GlobalTransform << std::endl;GlobalTransform = pairTransform * GlobalTransform;//保存配准对，转换到第一个点云框架中std::stringstream ss;ss << i << ".pcd";pcl::io::savePCDFile(ss.str(), *result, true);}
}配准函数
/**匹配一对点云数据集并且返还结果*参数 cloud_src 是源点云*参数 cloud_tgt 是目标点云*参数 output 输出的配准结果的源点云*参数 final_transform 是在来源和目标之间的转换*参数 downsample 是否需要进行下采样*/
void pairAlign(const PointCloud::Ptr cloud_src, const PointCloud::Ptr cloud_tgt, PointCloud::Ptr output, Eigen::Matrix4f &final_transform, bool downsample = false)
{//为了一致性和高速的下采样//注意：为了大数据集需要允许这项PointCloud::Ptr src(new PointCloud);PointCloud::Ptr tgt(new PointCloud);pcl::VoxelGrid<PointT> grid;//体素滤波// 是否先对点云进行下采样if (downsample){grid.setLeafSize(0.05, 0.05, 0.05);grid.setInputCloud(cloud_src);grid.filter(*src);grid.setInputCloud(cloud_tgt);grid.filter(*tgt);}else{src = cloud_src;tgt = cloud_tgt;}//计算曲面法线和曲率PointCloudWithNormals::Ptr points_with_normals_src(new PointCloudWithNormals);PointCloudWithNormals::Ptr points_with_normals_tgt(new PointCloudWithNormals);pcl::NormalEstimation<PointT, PointNormalT> norm_est;//点云法线估计对象// 使用KD树进行搜索//添加搜索算法 kdtree search 最近的几个点 估计平面 协方差矩阵PCA分解 求解法线pcl::search::KdTree<pcl::PointXYZ>::Ptr tree(new pcl::search::KdTree<pcl::PointXYZ>());norm_est.setSearchMethod(tree);norm_est.setKSearch(30); //设置最近邻居的数量k，k最近邻搜索norm_est.setInputCloud(src);norm_est.compute(*points_with_normals_src);//计算表面法线特征并保存结果pcl::copyPointCloud(*src, *points_with_normals_src);//不同类型的点云之间的转换norm_est.setInputCloud(tgt);norm_est.compute(*points_with_normals_tgt);pcl::copyPointCloud(*tgt, *points_with_normals_tgt);//举例说明我们自定义点的表示（以上定义）MyPointRepresentation point_representation;//调整'curvature'尺寸权重以便使它和x, y, z平衡float alpha[4] = { 1.0, 1.0, 1.0, 1.0 };point_representation.setRescaleValues(alpha);// 配准//IterativeClosestPointNonLinear是一个ICP变体，使用Levenberg-Marquardt优化后端。合成的转换矩阵被优化为四元数。pcl::IterativeClosestPointNonLinear<PointNormalT, PointNormalT> reg;reg.setTransformationEpsilon(1e-6);//设置收敛判断条件，数值越小则精度越大，收敛也越慢//将两个对应关系之间的(src<->tgt)最大距离设置为10厘米//注意：根据你的数据集大小来调整reg.setMaxCorrespondenceDistance(0.1);//大于10cm的点不考虑//设置点表示reg.setPointRepresentation(boost::make_shared<const MyPointRepresentation>(point_representation));reg.setInputCloud(points_with_normals_src);//原点云reg.setInputTarget(points_with_normals_tgt);//目标点云////在一个循环中运行相同的最优化并且使结果可视化Eigen::Matrix4f Ti = Eigen::Matrix4f::Identity(), prev, targetToSource;PointCloudWithNormals::Ptr reg_result = points_with_normals_src;reg.setMaximumIterations(2);//最大迭代次数，每次迭代两次就认为收敛//手动迭代，每手动迭代一次，在窗口对最新的迭代结果进行刷新显示for (int i = 0; i < 30; ++i){PCL_INFO("Iteration Nr. %d.\n", i);//为了可视化的目的保存点云points_with_normals_src = reg_result;//估计reg.setInputCloud(points_with_normals_src);reg.align(*reg_result);//在每一个迭代之间累积转换Ti = reg.getFinalTransformation() * Ti;//如果这次转换和之前转换之间的差异小于阈值//则通过减小最大对应距离来改善程序if (fabs((reg.getLastIncrementalTransformation() - prev).sum()) < reg.getTransformationEpsilon())reg.setMaxCorrespondenceDistance(reg.getMaxCorrespondenceDistance() - 0.001);prev = reg.getLastIncrementalTransformation();//可视化当前状态showCloudsRight(points_with_normals_tgt, points_with_normals_src);}//// 得到目标点云到源点云的变换targetToSource = Ti.inverse();////把目标点云转换回源框架pcl::transformPointCloud(*cloud_tgt, *output, targetToSource);p->removePointCloud("source");p->removePointCloud("target");PointCloudColorHandlerCustom<PointT> cloud_tgt_h(output, 0, 255, 0);//配准后的点云为红色PointCloudColorHandlerCustom<PointT> cloud_src_h(cloud_src, 255, 0, 0);//原始点云为绿色p->addPointCloud(output, cloud_tgt_h, "target", vp_2);p->addPointCloud(cloud_src, cloud_src_h, "source", vp_2);PCL_INFO("Press q to continue the registration.\n");p->spin();p->removePointCloud("source");p->removePointCloud("target");//添加源点云到转换目标*output += *cloud_src;final_transform = targetToSource;
}输入参数
- *参数 cloud_src 是源点云
- *参数 cloud_tgt 是目标点云
- *参数 output 输出的配准结果的源点云
- *参数 final_transform 是在来源和目标之间的转换
- *参数 downsample 是否需要进行下采样
下采样的选项是针对大规模点云而准备的，通过下采样可以提高点云配准的计算速度。
非线性ICP对象
IterativeClosestPointNonLinear是一个ICP变体，使用Levenberg-Marquardt优化后端。合成的转换矩阵被优化为四元数。
//IterativeClosestPointNonLinear是一个ICP变体，使用Levenberg-Marquardt优化后端。合成的转换矩阵被优化为四元数。pcl::IterativeClosestPointNonLinear<PointNormalT, PointNormalT> reg;reg.setTransformationEpsilon(1e-6);//设置收敛判断条件，数值越小则精度越大，收敛也越慢//将两个对应关系之间的(src<->tgt)最大距离设置为10厘米//注意：根据你的数据集大小来调整reg.setMaxCorrespondenceDistance(0.1);//大于10cm的点不考虑//设置点表示reg.setPointRepresentation(boost::make_shared<const MyPointRepresentation>(point_representation));reg.setInputCloud(points_with_normals_src);//原点云reg.setInputTarget(points_with_normals_tgt);//目标点云该算法具有多个终止条件：
- 迭代次数已达到用户设定的最大迭代次数（通过setMaximumIterations()函数）
- 先前的转换和当前估计的转换之间的差*小于用户施加的值（通过setTransformationEpsilon()函数）
- 欧几里得平方误差的总和小于用户定义的阈值
手动迭代
- 为了显示匹配过程中的迭代过程，ICP在内部进行计算时，限制其最大的迭代次数为2，即每迭代两次就认为收敛，停止内部迭代。
- 然后进行手动迭代，每首动迭代一次，在配准结果视口显示最新的配准结果。
- 在每次迭代过程中，记录并累积由ICP返回的转换矩阵。
- 如果迭代N次和迭代N-1次中找到的转换矩阵之间的差异小于传给ICP的变换收敛阈值，我们选择源和目标之间更靠近的对应点距离阈值来改善配准过程。
//在一个循环中运行相同的最优化并且使结果可视化Eigen::Matrix4f Ti = Eigen::Matrix4f::Identity(), prev, targetToSource;PointCloudWithNormals::Ptr reg_result = points_with_normals_src;reg.setMaximumIterations(2);//最大迭代次数，每次迭代两次就认为收敛//手动迭代，每手动迭代一次，在窗口对最新的迭代结果进行刷新显示for (int i = 0; i < 30; ++i){PCL_INFO("Iteration Nr. %d.\n", i);//为了可视化的目的保存点云points_with_normals_src = reg_result;//估计reg.setInputCloud(points_with_normals_src);reg.align(*reg_result);//在每一个迭代之间累积转换Ti = reg.getFinalTransformation() * Ti;//如果这次转换和之前转换之间的差异小于阈值//则通过减小最大对应距离来改善程序if (fabs((reg.getLastIncrementalTransformation() - prev).sum()) < reg.getTransformationEpsilon())reg.setMaxCorrespondenceDistance(reg.getMaxCorrespondenceDistance() - 0.001);prev = reg.getLastIncrementalTransformation();//可视化当前状态showCloudsRight(points_with_normals_tgt, points_with_normals_src);}实验结果
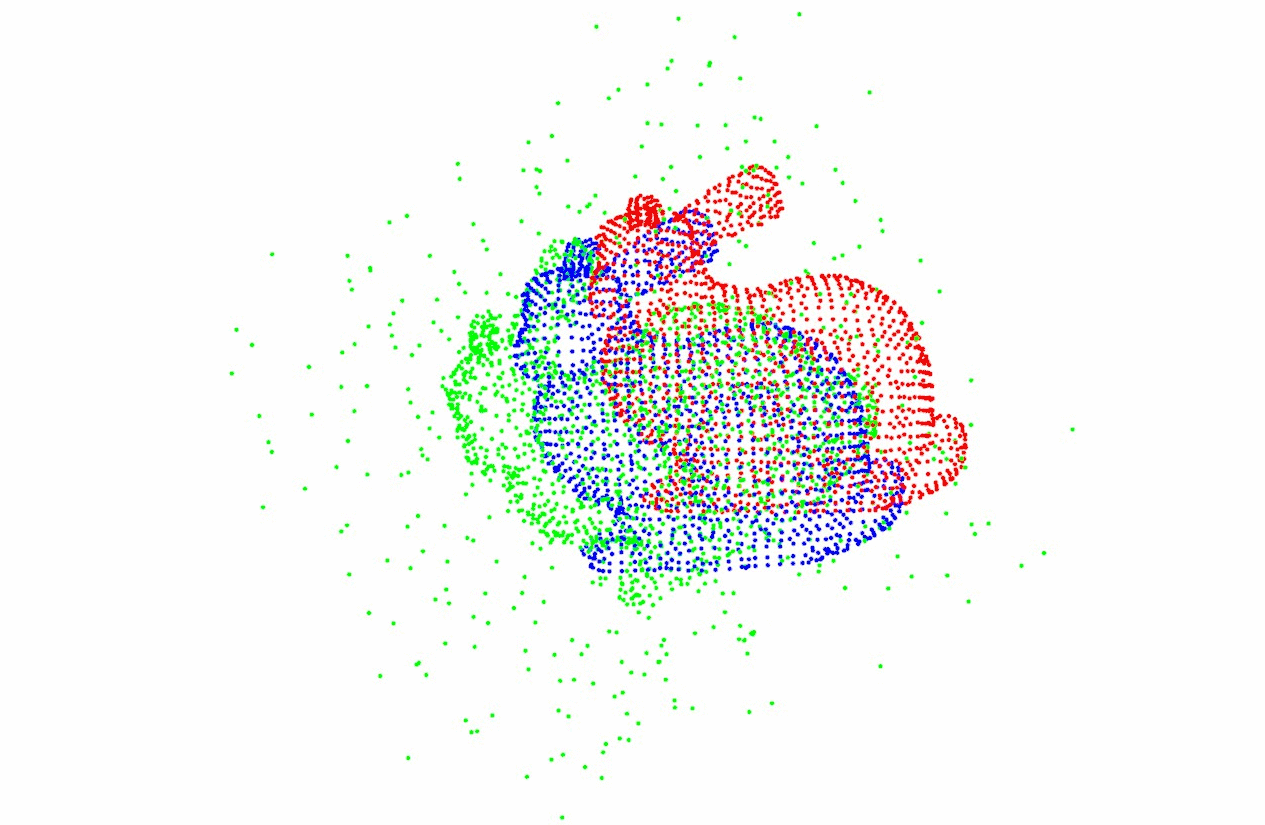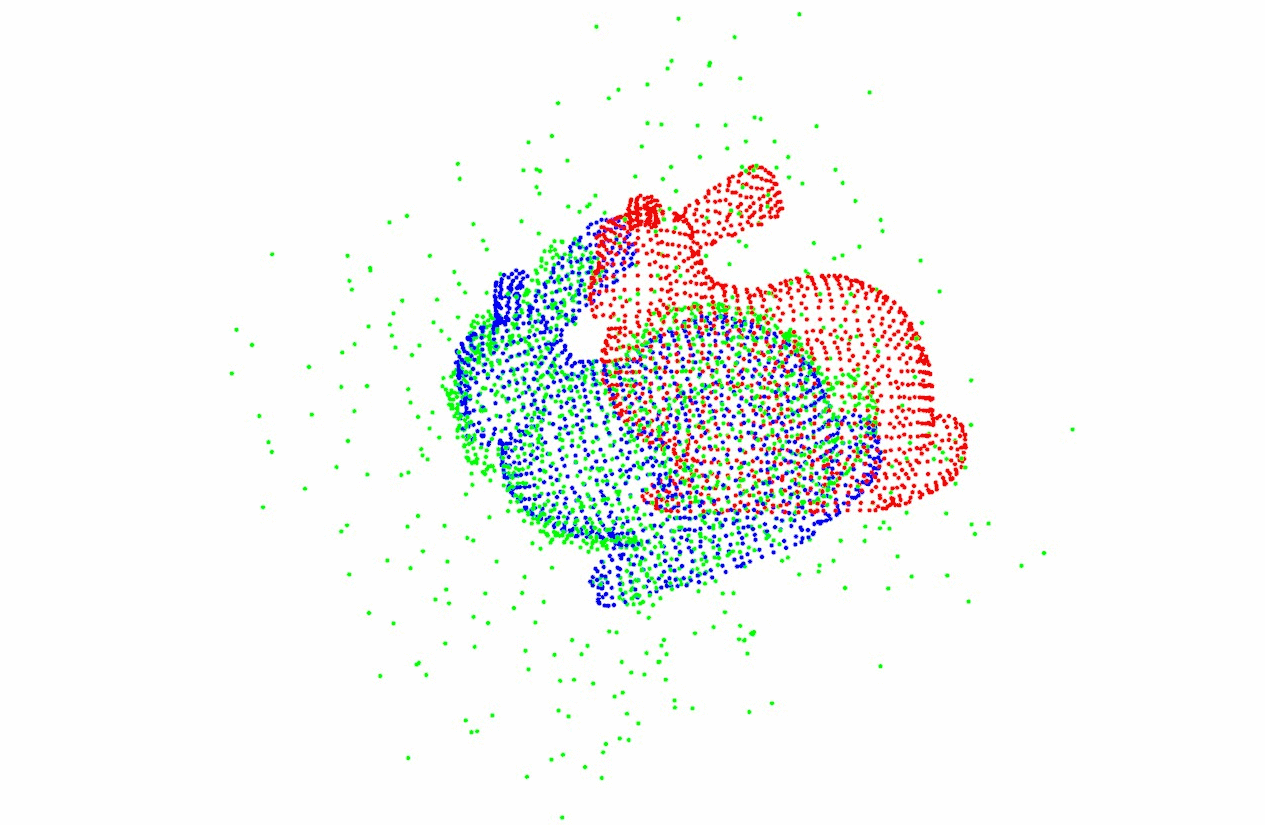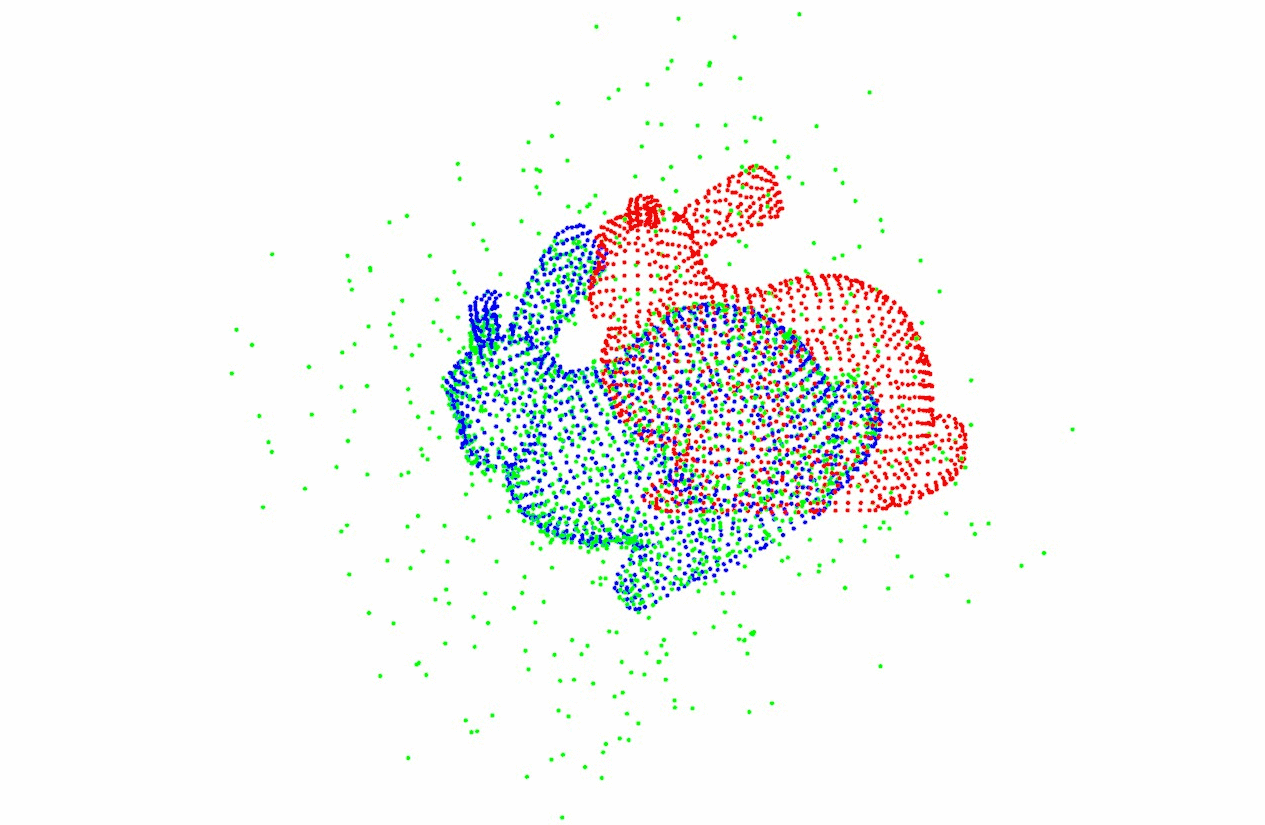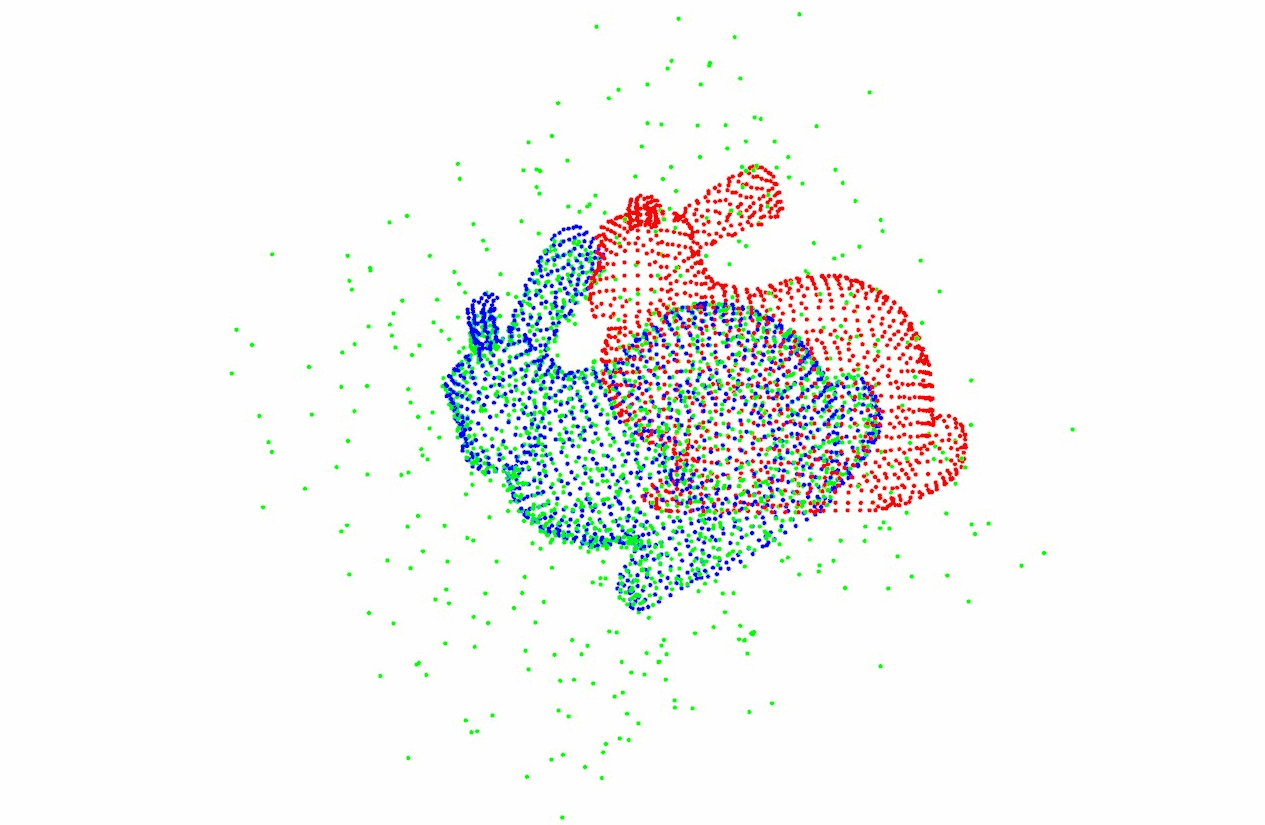
点云1和点云2：
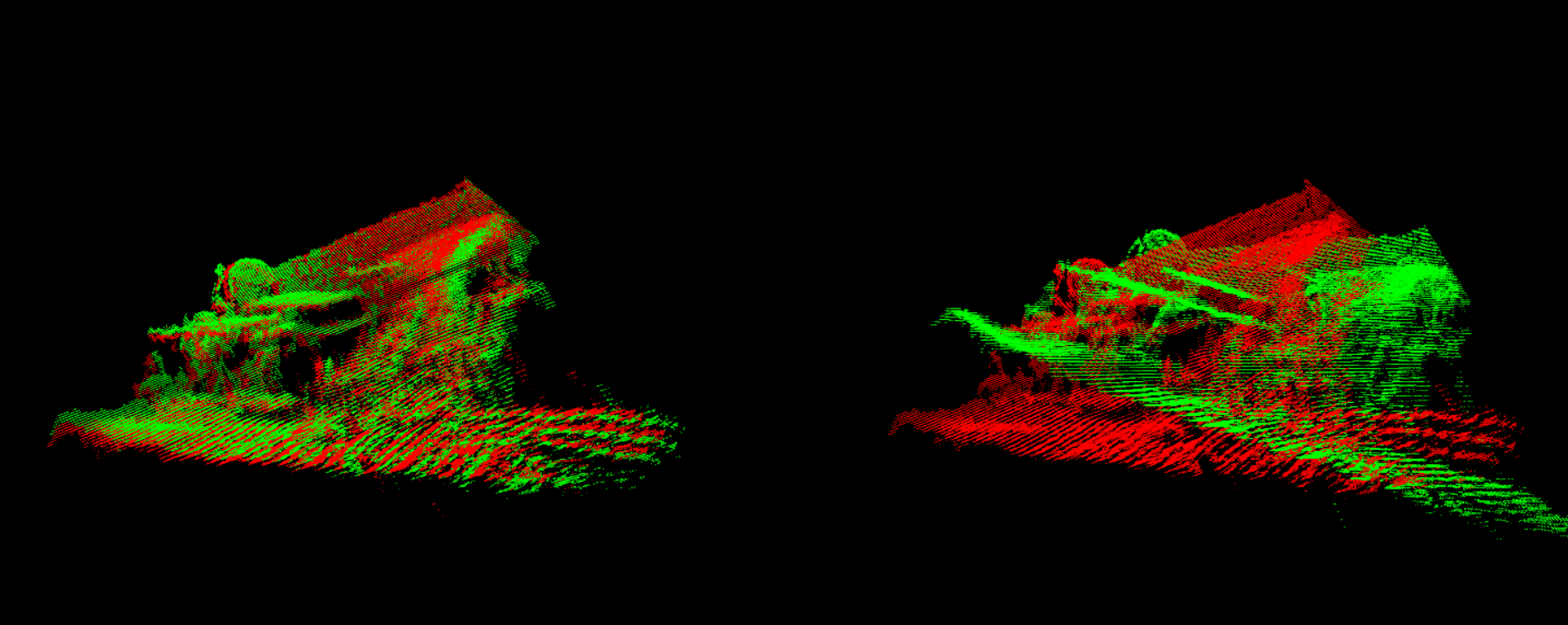
点云2和点云3：
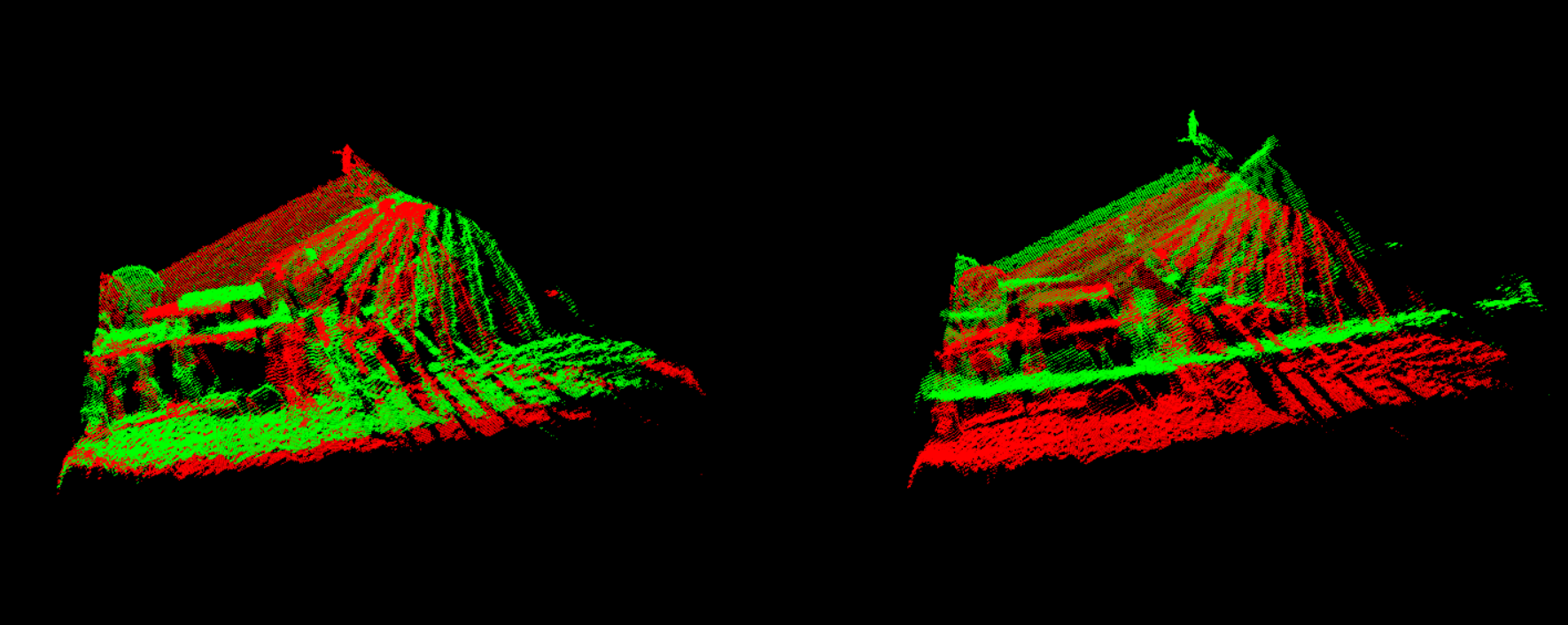点云3和点云4：
点云4和点云5：
结果打印：
Loaded 5 datasets.Press q to begin the registration.
Aligning capture0001.pcd (249647) with capture0002.pcd (249931).
Iteration Nr. 0.
Iteration Nr. 1.
Iteration Nr. 2.
Iteration Nr. 3.
Iteration Nr. 4.
Iteration Nr. 5.
Iteration Nr. 6.
Iteration Nr. 7.
Iteration Nr. 8.
Iteration Nr. 9.
Iteration Nr. 10.
Iteration Nr. 11.
Iteration Nr. 12.
Iteration Nr. 13.
Iteration Nr. 14.
Iteration Nr. 15.
Iteration Nr. 16.
Iteration Nr. 17.
Iteration Nr. 18.
Iteration Nr. 19.
Iteration Nr. 20.
Iteration Nr. 21.
Iteration Nr. 22.
Iteration Nr. 23.
Iteration Nr. 24.
Iteration Nr. 25.
Iteration Nr. 26.
Iteration Nr. 27.
Iteration Nr. 28.
Iteration Nr. 29.
Press q to continue the registration.
GlobalTransform:
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
Press q to begin the registration.
Aligning capture0002.pcd (249931) with capture0003.pcd (248494).
Iteration Nr. 0.
Iteration Nr. 1.
Iteration Nr. 2.
Iteration Nr. 3.
Iteration Nr. 4.
Iteration Nr. 5.
Iteration Nr. 6.
Iteration Nr. 7.
Iteration Nr. 8.
Iteration Nr. 9.
Iteration Nr. 10.
Iteration Nr. 11.
Iteration Nr. 12.
Iteration Nr. 13.
Iteration Nr. 14.
Iteration Nr. 15.
Iteration Nr. 16.
Iteration Nr. 17.
Iteration Nr. 18.
Iteration Nr. 19.
Iteration Nr. 20.
Iteration Nr. 21.
Iteration Nr. 22.
Iteration Nr. 23.
Iteration Nr. 24.
Iteration Nr. 25.
Iteration Nr. 26.
Iteration Nr. 27.
Iteration Nr. 28.
Iteration Nr. 29.
Press q to continue the registration.
GlobalTransform:
0.955226 0.0826862 0.284086 -1.06331
-0.0184208 0.974913 -0.22182 0.535996
-0.295301 0.206655 0.932787 0.196817
0 0 0 1
Press q to begin the registration.
Aligning capture0003.pcd (248494) with capture0004.pcd (244573).
Iteration Nr. 0.
Iteration Nr. 1.
Iteration Nr. 2.
Iteration Nr. 3.
Iteration Nr. 4.
Iteration Nr. 5.
Iteration Nr. 6.
Iteration Nr. 7.
Iteration Nr. 8.
Iteration Nr. 9.
Iteration Nr. 10.
Iteration Nr. 11.
Iteration Nr. 12.
Iteration Nr. 13.
Iteration Nr. 14.
Iteration Nr. 15.
Iteration Nr. 16.
Iteration Nr. 17.
Iteration Nr. 18.
Iteration Nr. 19.
Iteration Nr. 20.
Iteration Nr. 21.
Iteration Nr. 22.
Iteration Nr. 23.
Iteration Nr. 24.
Iteration Nr. 25.
Iteration Nr. 26.
Iteration Nr. 27.
Iteration Nr. 28.
Iteration Nr. 29.
Press q to continue the registration.
GlobalTransform:
0.949526 0.173744 0.261175 -1.1172
-0.062844 0.921082 -0.384264 1.12617
-0.307327 0.348455 0.885511 0.140448
0 0 0 1
Press q to begin the registration.
Aligning capture0004.pcd (244573) with capture0005.pcd (244977).
Iteration Nr. 0.
Iteration Nr. 1.
Iteration Nr. 2.
Iteration Nr. 3.
Iteration Nr. 4.
Iteration Nr. 5.
Iteration Nr. 6.
Iteration Nr. 7.
Iteration Nr. 8.
Iteration Nr. 9.
Iteration Nr. 10.
Iteration Nr. 11.
Iteration Nr. 12.
Iteration Nr. 13.
Iteration Nr. 14.
Iteration Nr. 15.
Iteration Nr. 16.
Iteration Nr. 17.
Iteration Nr. 18.
Iteration Nr. 19.
Iteration Nr. 20.
Iteration Nr. 21.
Iteration Nr. 22.
Iteration Nr. 23.
Iteration Nr. 24.
Iteration Nr. 25.
Iteration Nr. 26.
Iteration Nr. 27.
Iteration Nr. 28.
Iteration Nr. 29.
Press q to continue the registration.
GlobalTransform:
0.850072 0.467777 0.241993 -1.41569
-0.0251348 0.494991 -0.868535 2.55173
-0.526065 0.732235 0.432536 1.18894
0 0 0 1
