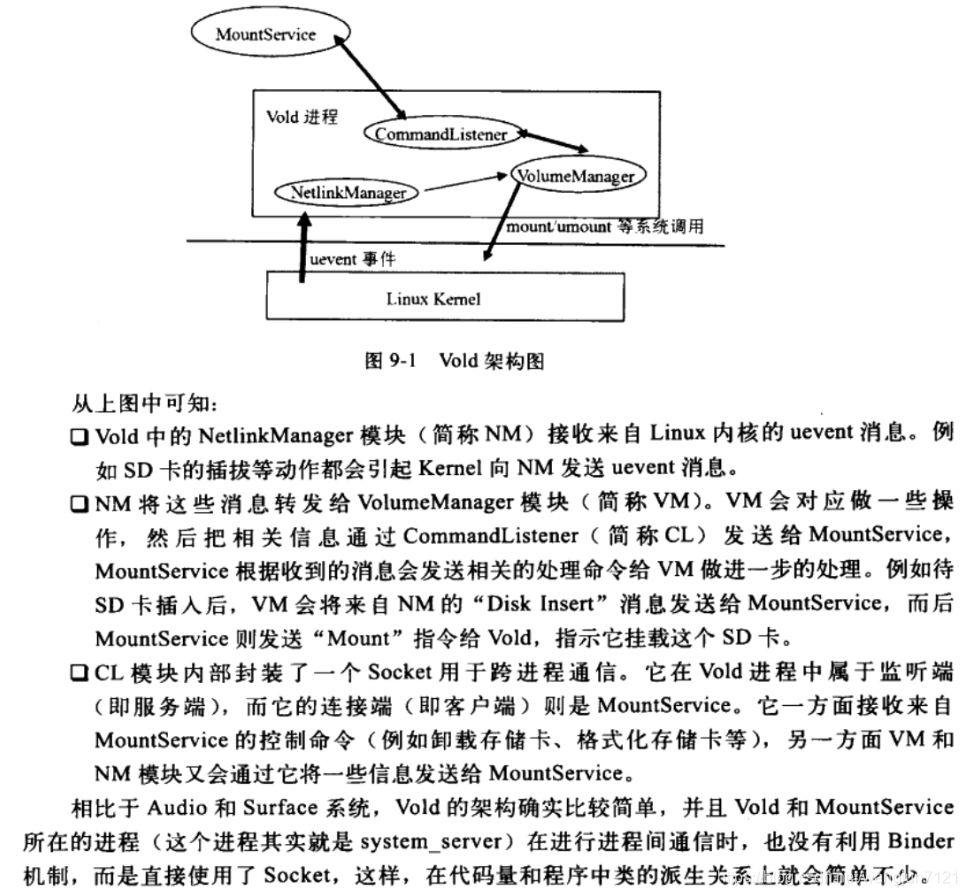
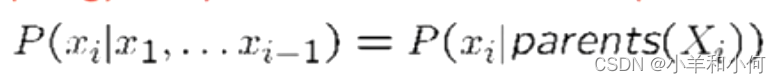贝叶斯网络系列学习（1）

文章目录

贝叶斯网络系列学习（1）
前言
一、基础知识
二、贝叶斯网络
- 1.朴素贝叶斯
- - 1.2 朴素贝叶斯的分类
- 2.贝叶斯网络
- - 2.1 贝叶斯网络
  - 2.2 代码
总结
参考文献

前言

最近一直在学习水下环境安全性态势评估，需要用到贝叶斯网络，因此，打算用Blog记录一下自己的学习笔记，也能方便以后的查找。

一、基础知识

1.联合概率
联合概率是包含多个条件，且所有的条件同时成立的概率。记作 $\ P(A,B)= P(AB) \$

2.条件概率
条件概率又称为似然概率，表示的是事件A在另一个事件B已经发生下的发生概率，多个事件的时候，需要基于各个事件的条件独立假设。记作 $\ P(A|B)= \frac{P(A,B)}{P(B)} = \frac{P(A)P(B|A)} {P(B)} \$

3.先验概率
一般是单独事件发生的概率，例如P(A)，P(B)等。先验概率可以是基于历史数据的统计，可以由背景常识得出，也可以是根据人的主观观点获得。

4.后验概率
若P(X|Y)为正向，则P(Y|X)为反向，基于先验概率求得反向条件概率，在形式上与条件概率相同。

5.贝叶斯公式
$\ P(Y|X)= \frac{P(Y)P(X|Y)} {P(X)} \$

其中，P(Y|X)为后验概率，一般为求解的目标；P(X|Y)为条件概率（又叫做似然概率），一般是通过历史数据统计获得；P(X)、P(Y)为先验概率。

二、贝叶斯网络

1.朴素贝叶斯

朴素贝叶斯是以贝叶斯定理为基础并且假设特征条件之间相互独立的方法，先通过给定的训练集，以特征之间独立为前提条件假设，学习从输入到输出之间的联合概率分布，在基于学习到的数据模型，根据新的输入X求出使得后验概率最大的输出Y。其中朴素一词指的是条件独立，就意味着两个事件同时发生的概率即等于两个事件分别发生的概率乘积，即
$\ P(A,B)= P(A)*P(B) \$

因此，朴素贝叶斯算法可以表示为：

$\ P(y|x1,x2,...,xn)= \frac{P(y)P(x1,x2,...,xn|y)} {P(x1,x2,...,xn)} \$

朴素贝叶斯在进行分类的时候不是直接返回分类，而是返回所属某个分类的概率。由于朴素贝叶斯假设特征条件之间相互独立，所以有

$\ P(y|x1,x2,...,xn)= argmax \frac{P(y)*P(x1|y)*P(x2|y)*...*P(xn|y)} {\Sigma P(yi)*P(x1|yi)*P(x2|yi)*...*P(xn|yi)} \$

1.2 朴素贝叶斯的分类

（1）高斯朴素贝叶斯（GaussianNB）:可应用于任意连续数据，每个特征的属性的取值为连续变量。我们重点关注一下特征取值为连续变量的形式，对于数据是连续属性可以考虑概率密度函数，特征的似然被假设为高斯分布，其条件概率函数就可以表示为：

$\ P(xi|y) = \frac{1} {\sqrt {2 \pi} \sigma_{y,i}} exp(- \frac {(x_i- \mu_{y,i} )^2} {2 \sigma_{y,i}^2})$
其中， $\sigma$ 是样本的方差， $\mu$ 是样本的均值。所以，对于特征变量取值是连续的可以采用高斯公式计算条件概率函数，只需要计算出样本的均值和方差即可，求解条件概率是比较方便的。

（2）多项式朴素贝叶斯（MultinomialNB）:假定输入数据为计数数据（即每个特征代表某个对象的整数计数），每个特征的属性的取值都是频数。

（3）伯努利朴素贝叶斯（BernoulliNB）:假定输入数据为二分类数据，每个特征的属性的取值都是布尔型。

2.贝叶斯网络

2.1 贝叶斯网络

在生活中，我们研究的随机变量并不是都是相互独立的，它们之间可能是相互有关系，也就是说若干的样本之间并不是相互独立，可能产生了某种关系，最后看起来像是一个网，我们把这样的一个有向无环图叫做贝叶斯网络。

贝叶斯网络它是一个有向无环图，它的结点表示的是一些随机变量，这些随机变量有些是可被观测到的，有些是无法观测到的，它用概率值表示两个观测值之间的关系。贝叶斯网络具有强大的不确定性问题的处理能力，用条件概率表达各个信息要素之间的相关关系，能够在有限的、不完整的、不确定的信息条件下进行学习和推理，此外，通过贝叶斯网络进行学习和推理还能够实现多源信息的表达和融合。

2.2 代码

这里建议大家使用pgmpy进行实现贝叶斯网络，

1、创建贝叶斯网络
在 pgmpy中，定义一个贝叶斯网的流程一般是先建立网络结构，然后填入相关参数。

2、创建网络结构
这里以最经典的肺癌例子为基础进行展示。
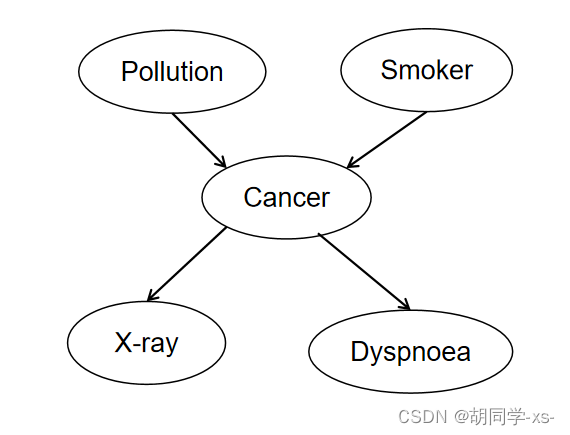
在这里插入图片描述

# 创建网络结构
cancer_model = BayesianModel([('Pollution', 'Cancer'),('Smoker', 'Cancer'),('Cancer', 'Xray'),('Cancer', 'Dyspnoea')])

3、填入参数
我认为这一步是最关键、最重要的地方，通过样本进行学习到对应的条件概率，当条件概率给的愈加准确，后续的推测结果也就愈加精准。

样本数据并不能代表全部数据的情况，现实生活中我们有些事情就是不能用枚举法进行穷尽样本数据。因此，我们可以采用极大似然估计，用现有的样本数据进行评估不能穷尽的数据的概率。

对于条件概率，我更加偏向于融合专家经验和样本数据的学习后习的。当然，这仅仅就是目前自己的一个想法，具体的实现还要结合项目的具体情况，后续有了新的想法还会不断的更新。

# 设置参数
cpd_poll = TabularCPD(variable='Pollution', variable_card=2,values=[[0.9], [0.1]])
cpd_smoke = TabularCPD(variable='Smoker', variable_card=2,values=[[0.3], [0.7]])
cpd_cancer = TabularCPD(variable='Cancer', variable_card=2,values=[[0.03, 0.05, 0.001, 0.02],[0.97, 0.95, 0.999, 0.98]],evidence=['Smoker', 'Pollution'],evidence_card=[2, 2])
cpd_xray = TabularCPD(variable='Xray', variable_card=2,values=[[0.9, 0.2], [0.1, 0.8]],evidence=['Cancer'], evidence_card=[2])
cpd_dysp = TabularCPD(variable='Dyspnoea', variable_card=2,values=[[0.65, 0.3], [0.35, 0.7]],evidence=['Cancer'], evidence_card=[2])
cancer_model.add_cpds(cpd_poll, cpd_smoke, cpd_cancer, cpd_xray, cpd_dysp)

4、网络推理
构建了贝叶斯网之后, 我们使用贝叶斯网来进行推理.，推理算法分精确推理和近似推理。贝叶斯网络模型的推理（inference）问题是通过计算回答查询（query）的过程。根据已知变量（通常称为证据变量（evidence variables）），计算其后验概率分布的变量（通常称为查询变量（query variables））。其中推理的方式有很多种，这里我就仅列举了常用的三种方法，大家有兴趣可以去pgmpy官网上找找，寻找一个适合自己项目的推理方法。

print('=====================变量消除法============================')
asia_infer = VariableElimination(cancer_model)
q = asia_infer.query(variables=['Cancer'], evidence={'Smoker': 0, 'Pollution': 1, 'Xray': 1, 'Dyspnoea': 0})
print(q)
print('======================因果推理法===========================')infer_adjusted = CausalInference(cancer_model)
q1 = infer_adjusted.query(variables=['Cancer'], evidence={'Smoker': 0, 'Pollution': 1, 'Xray': 1, 'Dyspnoea': 0})
print(q1)print('======================信念传播法===========================')
bp = BeliefPropagation(cancer_model)
ans = bp.query(variables=['Cancer'], evidence={'Smoker': 0, 'Pollution': 1, 'Xray': 1, 'Dyspnoea': 0})
print(ans)

总结

贝叶斯网络的应用十分广泛，可以很好地利用对因果关系的理解把一些先验知识编码到模型中，也可以利用收集到的样本数据信息去修正和改变模型本身，从而能够实现更加精准的推理。

每一次写一篇都是为了让自己有更深的思考，当然也希望你们能读懂。加油，兄弟们！

参考文献

[1] 周志华，机器学习，清华大学出版社，2016
[2] https://pinvondev.github.io/tags/%E8%B4%9D%E5%8F%B6%E6%96%AF%E7%BD%91/
[3] https://blog.csdn.net/qq_35290785/article/details/93539124