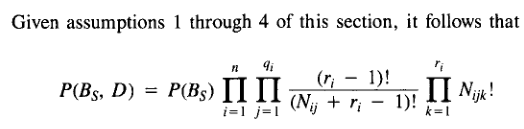文章目录
- 1. 完备数据的结构学习
- 基于评分搜索
- 定义
- 评分函数
- 基于贝叶斯统计的评分
- K2评分
- BD(Bayesian Dirichlet)评分
- BDeu(Bayesian Dirichlet eu)评分
- 基于信息理论的评分
- MDL评分函数
- AIC评分函数
- MIT评分函数
- 搜索方法
- K2算法
- 爬山(hillclimbing)算法
- GES (greedy equivalent search)算法
- 基于约束|依赖统计
- 基于分解
- 基于Markov blanket
- 基于空间结构限制
- 2. 不完备数据结构学习
- 参考
1. 完备数据的结构学习
基于评分搜索
定义
基于评分搜索的方法将BN结构学习视为组合优化问题;
- 首先通过定义评分函数对BN结构空间中的不同元素与样本数据的拟合程度进行度量
- 然后利用搜索算法确定评分最高的网络结构,即与数据拟合最好的网络结构
BN结构学习可定义为优化模型:
O M = ( G , Ω , F ) OM=(G, \Omega, F) OM=(G,Ω,F)
G:候选网络结构搜索空间,它定义了样本数据集D中所有变量(节点)之间可能连接关系的网络结构集合;
Ω \Omega Ω:网络变量之间需要满足的约束条件集合,最基本的约束是所有节点间的连接构成一个有向无环图;
F:评分函数,表示从搜索空间G到实数集R的一个映射,函数的极值点即为网络的最优结构.
Robinson等证明了包含n个节点可能的BN结构数目 f ( n ) f(n) f(n):
f ( n ) = ∑ i = 1 n n ! i ! ( n − i ) ! 2 i ( n − i ) f ( n − i ) f(n)=\sum^n_{i=1}\frac{n!}{i!(n-i)!}2^{i(n-i)}f(n-i) f(n)=i=1∑ni!(n−i)!n!2i(n−i)f(n−i)
可见,随着变量数目的增多,搜索空间的维数呈 指数级 增长,因此,评分函数和搜索策略是影响评分搜索算法的主要因素.
评分函数
在BN结构学习的框架中,结构G和参数 θ G \theta_G θG被视为随机变量;
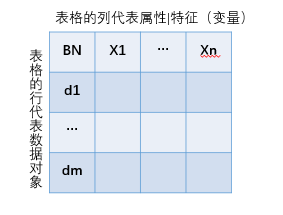
假设数据集 D = ( d 1 , d 2 , . . . , d m ) D=(d_1,d_2, . . ., d_m) D=(d1,d2,...,dm)是关于n个变量 { X 1 , X 2 , . . . , X n } \{X_1, X_2,..., X_n\} {X1,X2,...,Xn}的样本;
G的可能取值包括所有以 { X 1 , X 2 , . . . , X n } \{X_1, X_2,..., X_n\} {X1,X2,...,Xn}为节点的有向无环图。
给定结构G,变量 θ G \theta_G θG的可能取值是与G对应的参数值。
结构先验分布: P ( G ) P(G) P(G)
结构确定之后, θ G \theta_G θG 的参数先验分布: P ( θ G ) P(\theta_G) P(θG)
评分函数的输入与输出:
"""
input:Vi:某一变量(属性|特征)pa(Vi):Vi的父节点集合,第一次调用时候为 emptyD:数据集
output:pa(Vi):此次评分中Vi分数最高的父节点集合score:评分
"""
def Ranking(Vi,pa(Vi),D):passreturn score,pa(Vi)
基于贝叶斯统计的评分
假设数据集D是关于样本变量 { X 1 , X 2 , . . . , X n } \{X_1, X_2,..., X_n\} {X1,X2,...,Xn} 完整独立同分布数据。
贝叶斯评分的主要思想是给定先验知识和样本数据条件下,选择一个后验概率值最大的网络结构,即:
1-1
G ∗ = arg m a x G P ( G ∣ D ) G^* = \arg max_GP(G|D) G∗=argmaxGP(G∣D)
重点是 P ( G ∣ D ) P(G|D) P(G∣D),又根据贝叶斯定理:
1-2
P ( G ∣ D ) = P ( D ∣ G ) P ( G ) P ( D ) P(G|D)=\frac{P(D|G)P(G)}{P(D)} P(G∣D)=P(D)P(D∣G)P(G)
P ( G , D ) = P ( G ∣ D ) P ( D ) = P ( D ∣ G ) P ( G ) P(G,D)= P(G|D)P(D)=P(D|G)P(G) P(G,D)=P(G∣D)P(D)=P(D∣G)P(G)
P ( D ) P(D) P(D)已知而且不依赖 P ( G ) P(G) P(G),所以 P ( G ∣ D ) P(G|D) P(G∣D)可转换为:
1-3
log P ( G , D ) = log P ( D ∣ G ) + log P ( G ) \log P(G,D) = \log P(D|G) + \log P(G) logP(G,D)=logP(D∣G)+logP(G)
则:
1-4
G ∗ = arg log P ( D ∣ G ) + log P ( G ) G^* = \arg \log P(D|G)+\log P(G) G∗=arglogP(D∣G)+logP(G)
P ( G ) P(G) P(G)是结构先验分布,一般会假设它是某种分布,ex:均匀分布
之后展开 P ( D ∣ G ) P(D|G) P(D∣G) (称为边缘似然函数)。
1-5
P ( D ∣ G ) = ∫ P ( D ∣ G , θ G ) p ( θ G ∣ G ) d θ G P(D|G)=\int P(D|G,\theta_G)p(\theta_G|G) d \theta_G P(D∣G)=∫P(D∣G,θG)p(θG∣G)dθG
K2评分
假设数据集D是关于样本变量 { X 1 , X 2 , . . . , X n } \{X_1, X_2,..., X_n\} {X1,X2,...,Xn} 完整独立同分布数据。G是关于变量集 { X 1 , X 2 , . . . , X n } \{X_1, X_2,..., X_n\} {X1,X2,...,Xn}的BN结构,并且 p ( θ G ∣ G ) p(\theta_G|G) p(θG∣G)服从均匀分布。
可知如下K2评分:
1-6
F K 2 ( G ∣ D ) = log P ( G ) + ∑ i = 1 n ∑ j = 1 q i { log ( r i − 1 ) ! ( m i j ∗ + r i − 1 ) ! ∑ k = 1 r i log ( m i j k ! ) } F_{K2}(G|D)=\log P(G) + \sum_{i=1}^n\sum_{j=1}^{q_i}\{\log\frac{(r_i-1)!}{(m_{ij*}+r_i-1)!}\sum_{k=1}^{r_i} \log (m_{ijk}!)\} FK2(G∣D)=logP(G)+i=1∑nj=1∑qi{log(mij∗+ri−1)!(ri−1)!k=1∑rilog(mijk!)}
当结构的先验分布为均匀分布时候, log P ( G ) = 0 \log P(G)=0 logP(G)=0
D:数据集
G:关于变量集 { X 1 , X 2 , . . . , X n } \{X_1, X_2,..., X_n\} {X1,X2,...,Xn}的BN结构
n:样本变量数目
i: 第i个X变量, X i X_i Xi
j: X i X_i Xi父节点的第j个取值
k: X i X_i Xi的第k个取值
p a ( V i ) : X i pa(V_i):X_i pa(Vi):Xi的父节点集合 ???
q i : q_i: qi:节点 X i X_i Xi 的父节点的取值数目
r i : X i r_i:X_i ri:Xi 取值数目, ( v i 1 , v i 1 , . . . , v i r i ) (v_{i1}, v_{i1}, ..., v_{ir_i}) (vi1,vi1,...,viri)
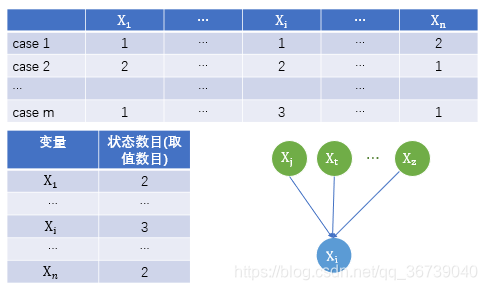
m i j k : m_{ijk}: mijk:表示节点 X i X_i Xi 取值为 v i k v_{ik} vik ,并且 X i X_i Xi 的父节点为第j个取值时候,对应的case记录数目;(NOTE:i:第i个变量,j:第i个变量 X i X_i Xi对应的父节点第j个取值,k: X i X_i Xi的第k个取值)
m i j ∗ = ∑ k = 1 r i log ( m i j k ) m_{ij*}=\sum_{k=1}^{r_i} \log (m_{ijk}) mij∗=∑k=1rilog(mijk):包含节点 X i X_i Xi 的所有取值,并且 X i X_i Xi 的父节点第j个取值时,对应的case记录数目例子链接
参考文章(知乎_抓好污水治理)
这句话很内核了:
对于每一种结构,统计所有可能组合的观测值在数据集中出现的次数,如结构2:x1=0, x3=0出现了10次,x1=1, x3=2出现了2次等等。然后利用这些统计信息计算这种结构的得分(一大堆推导公式,最后得出此得分与P(贝叶斯网络结构|数据集)正相关)。这个得分的含义就是得分越高,这个数据集下出现此结构的概率越高。然后挑选最大得分的结构作为此变量的结构。用此方法得出了每个变量的父节点,这样就得出了整体的贝叶斯网络结构。
参考文章(CSDN_jbb0523)
贝叶斯网络结构学习之K2算法(基于FullBNT-1.0.4的MATLAB实现)
[参考文献]
Cooper, G. F., & Herskovits, A Bayesian Method for the Induction of Probabilistic Networks from Data. E. (1992). Machine Learning, 9(4), 309–347. doi:10.1023/a:1022649401552
Note:网上的信息太乱了,很多参数含义都解释的不同,最好看原文
BD(Bayesian Dirichlet)评分
假设数据集D是关于样本变量 { X 1 , X 2 , . . . , X n } \{X_1, X_2,..., X_n\} {X1,X2,...,Xn} 完整独立同分布数据。G是关于变量集 { X 1 , X 2 , . . . , X n } \{X_1, X_2,..., X_n\} {X1,X2,...,Xn}的BN结构,并且 p ( θ G ∣ G ) p(\theta_G|G) p(θG∣G)服从Dirichlet分布。
p ( θ G ∣ G ) ∝ ∏ i = 1 n ∏ j = 1 q i ∏ k = 1 r i θ i j k α i j k − 1 p(\theta_G|G) \propto \prod^n_{i=1} \prod^{q_i}_{j=1} \prod^{r_i}_{k=1}\theta_{ijk}^{\alpha_{ijk}-1} p(θG∣G)∝i=1∏nj=1∏qik=1∏riθijkαijk−1
可知如下BD评分:
F B D ( G ∣ D ) = log P ( G ) + ∑ i = 1 n { ∑ j = 1 q i { log Γ ( α i j ∗ ) Γ ( α i j ∗ + m i j ∗ ) + ∑ k = 1 r i log Γ ( α i j k + m i j k ) Γ ( α i j ∗ ) } F_{BD}(G|D)=\log P(G) + \sum_{i=1}^n\{\sum_{j=1}^{q_i}\{\log\frac{\Gamma(\alpha_{ij*})}{\Gamma(\alpha_{ij*}+m_{ij*})}+\sum_{k=1}^{r_i} \log \frac{\Gamma(\alpha_{ijk}+m_{ijk})}{\Gamma(\alpha_{ij*})}\} FBD(G∣D)=logP(G)+i=1∑n{j=1∑qi{logΓ(αij∗+mij∗)Γ(αij∗)+k=1∑rilogΓ(αij∗)Γ(αijk+mijk)}
D:数据集
G:关于变量集 { X 1 , X 2 , . . . , X n } \{X_1, X_2,..., X_n\} {X1,X2,...,Xn}的BN结构
n:样本变量数目
q i : q_i: qi:节点 X i X_i Xi 的父节点的取值数目
r i : X i r_i:X_i ri:Xi 取值数目, ( v i 1 , v i 1 , . . . , v i r i ) (v_{i1}, v_{i1}, ..., v_{ir_i}) (vi1,vi1,...,viri)
α i j k : \alpha_{ijk}: αijk:Dirichlet分布中的超参数取值
α i j ∗ = ∑ k = 1 r i α i j k \alpha_{ij*} = \sum_{k=1}^{r_i}\alpha_{ijk} αij∗=∑k=1riαijk
m i j k : m_{ijk}: mijk:表示节点 X i X_i Xi 取值为 v i k v_{ik} vik ,并且 X i X_i Xi 的父节点为第j个取值时候,对应的case记录数目;(NOTE:i:第i个变量,j:第i个变量 X i X_i Xi对应的父节点第j个取值,k: X i X_i Xi的第k个取值)
m i j ∗ = ∑ k = 1 r i log ( m i j k ) m_{ij*}=\sum_{k=1}^{r_i} \log (m_{ijk}) mij∗=∑k=1rilog(mijk):包含节点 X i X_i Xi 的所有取值,并且 X i X_i Xi 的父节点第j个取值时,对应的case记录数目
p a ( X i ) pa(X_i) pa(Xi): X i X_i Xi的父节点集合
θ i j k : \theta_{ijk}: θijk:???
Γ : \Gamma: Γ:gamma函数
迪利克雷分布介绍_知乎
所有的超参数值 α i j k = 1 \alpha_{ijk}=1 αijk=1时,BD评分退化为K2评分。
通常情况下,我们说的分布都是关于某个参数的函数,把对应的参数换成一个函数(函数也可以理解成某分布的概率密度)就变成了关于函数的函数
BDeu(Bayesian Dirichlet eu)评分
BD公式中的超参数 α i j k = α P ( X i = k , p a ( X i ) = j ∣ G ) \alpha_{ijk}=\alpha P(X_i=k,pa(X_i)=j | G) αijk=αP(Xi=k,pa(Xi)=j∣G)时候, P ( . ∣ G ) P(.|G) P(.∣G)表示网络G的先验分布, α \alpha α 表示先验样本等价量。
P ( X i = k , p a ( X i ) = j ∣ G ) = 1 r i q i P(X_i=k,pa(X_i)=j | G) = \frac{1}{r_iq_i} P(Xi=k,pa(Xi)=j∣G)=riqi1,即结构先验信息服从均匀分布。
可知如下BDeu评分:
F B D e u ( G ∣ D ) = log P ( G ) + ∑ i = 1 n ∑ j = 1 q i { log Γ ( α q i ) Γ ( m i j ∗ + α q i ) } + ∑ k = 1 r i log Γ ( m i j k + α r i q i ) Γ ( α r i q i ) F_{BDeu}(G|D)=\log P(G) + \sum_{i=1}^n\sum_{j=1}^{q_i}\{\log\frac{\Gamma(\frac{\alpha}{q_i})}{\Gamma(m_{ij*}+\frac{\alpha}{q_i})}\}+\sum_{k=1}^{r_i} \log \frac{\Gamma(m_{ijk}+\frac{\alpha}{r_iq_i})}{\Gamma(\frac{\alpha}{r_iq_i})} FBDeu(G∣D)=logP(G)+i=1∑nj=1∑qi{logΓ(mij∗+qiα)Γ(qiα)}+k=1∑rilogΓ(riqiα)Γ(mijk+riqiα)
基于信息理论的评分
基于信息理论的评分函数主要是利用编码理论和信息论中的最小描述长度(Minimum Description Length, MDL)原理来实现的.其基本思想源自对数据的存储。
假设D是一组给定的实例数据,如果要对其进行保存,为了节省存储空间,一般采用某种模型对其进行编码压缩,然后再保存压缩后的数据;另外,为了在需要的时候可以完全恢复这些实例数据,要求对所使用的模型进行保存;
因此,需要保存的数据长度=压缩后的数据长度+模型的描述长度,该长度称为总的描述长度。
MDL原理就是要求选择总描述长度最小的模型。按照MDL原理,BN结构学习就是要找到使得网络的描述长度和样本的编码长度之和最小的图模型。
这意味着MDL评分准则趋向于寻找一个结构较简单的网络,实现网络精度与复杂度之间的均衡。一般利用参数个数作为网络结构复杂度的惩罚函数:
2-1:
C ( G ) = 1 2 log m ∑ i = 1 n ( r i − 1 ) q i C(G) = \frac{1}{2}\log m\sum^n_{i=1}(r_i-1)q_i C(G)=21logmi=1∑n(ri−1)qi
m:数据集D中的样本总量;
∑ i = 1 n ( r i − 1 ) q i \sum^n_{i=1}(r_i-1)q_i ∑i=1n(ri−1)qi:网络中包含的参数总量
采用海明码表示压缩后的数据长度,就是关于数据D和模型的对数似然:
2-2:
L L D ( G ) = ∑ j = 1 n ∑ j = 1 q i ∑ k = 1 r i m i j k log ( m i j k m i j ∗ ) LL_D(G)=\sum^n_{j=1}\sum^{q_i}_{j=1}\sum^{r_i}_{k=1}m_{ijk}\log(\frac{m_{ijk}}{m_{ij*}}) LLD(G)=j=1∑nj=1∑qik=1∑rimijklog(mij∗mijk)
MDL评分函数
则由2-1、2-2可知,得到相应的MDL评分函数
2-3
F M D L ( G ∣ D ) = L L D ( G ) − C ( G ) F_{MDL}(G|D)=LL_D(G)-C(G) FMDL(G∣D)=LLD(G)−C(G)
2-4
F M D L ( G ∣ D ) = ∑ i = 1 n ∑ j = 1 q i ∑ k = 1 r i m i j k log ( m i j k m i j ∗ ) − 1 2 log m ∑ i = 1 n ( r i − 1 ) q i F_{MDL}(G|D)=\sum^n_{i=1}\sum^{q_i}_{j=1}\sum^{r_i}_{k=1}m_{ijk}\log(\frac{m_{ijk}}{m_{ij*}})- \frac{1}{2}\log m\sum^n_{i=1}(r_i-1)q_i FMDL(G∣D)=i=1∑nj=1∑qik=1∑rimijklog(mij∗mijk)−21logmi=1∑n(ri−1)qi
m:数据集D中的样本总量;
∑ i = 1 n ( r i − 1 ) q i \sum^n_{i=1}(r_i-1)q_i ∑i=1n(ri−1)qi:网络中包含的参数总量
AIC评分函数
MDL评分函数不依赖于先验概率;对给定的充分大的独立样本而言,具有最大MDL分值的网络可以任意接近于抽样分布;当实例数据D服从多项分布时,MDL评分函数等于BIC评分函数.因此对公式(2-4)做进一步的简化,得到AIC评分函数:
2-5
F A I C ( G ∣ D ) = ∑ i = 1 n ∑ j = 1 q i ∑ k = 1 r i m i j k log ( m i j k m i j ∗ ) − ∑ i = 1 n ( r i − 1 ) q i F_{AIC}(G|D)=\sum^n_{i=1}\sum^{q_i}_{j=1}\sum^{r_i}_{k=1}m_{ijk}\log(\frac{m_{ijk}}{m_{ij*}})- \sum^n_{i=1}(r_i-1)q_i FAIC(G∣D)=i=1∑nj=1∑qik=1∑rimijklog(mij∗mijk)−i=1∑n(ri−1)qi
MIT评分函数
MDL评分函数中,对网络的惩罚项用整个网络包含的参数以及样本数据量来表示,Campos结合贝叶斯网络的可分解性,用网络的局部结构复杂度作为惩罚项,提出一种基于互信息和卡方分布 的 MIT ( Mutual Information Tests) 评分函数.
2-6
F M I T ( G ∣ D ) = ∑ i = 1 , P a ( X − i ) ! = ∅ n ( 2 m M I D ( X i , P a ( X i ) ) − max σ i ∑ j = 1 S i χ α , l i σ i ( j ) ) F_{MIT}(G|D)=\sum^n_{i=1,Pa(X-i)!=\empty}(2mMI_D(X_i,Pa(X_i))-\max_{\sigma_i }\sum^{S_i}_{j=1}\chi_{\alpha,l_{i\sigma_i(j)}}) FMIT(G∣D)=i=1,Pa(X−i)!=∅∑n(2mMID(Xi,Pa(Xi))−σimaxj=1∑Siχα,liσi(j))
M I D ( X i , P a ( X i ) ) MI_D(X_i,Pa(X_i)) MID(Xi,Pa(Xi)): X i X_i Xi与其父变量之间互信息
p a ( X i ) pa(X_i) pa(Xi): X i X_i Xi的父节点集合
S i S_i Si: X i X_i Xi父节点的个数
χ α , l i σ i ( j ) \chi_{\alpha,l_{i\sigma_i(j)}} χα,liσi(j):表示置信度为 α \alpha α,自由度为 l i σ i ( j ) l_{i\sigma_i(j)} liσi(j)的卡方分布值。
搜索方法
求出每个变量评分函数最大的父变量集。
- K2算法
- 爬山算法
- GES算法
- 基于进化计算的方法
K2算法
K2算法使用贪心搜索去获取最大值。首先假设随机变量是有顺序的,如果 X i X_i Xi在 X j X_j Xj之前,那么不能存在从 X j X_j Xj到 X i X_i Xi的边。同时假设每个变量最多的父变量个数为u。每次挑选使评分函数最大的父变量放入集合,当无法使评分函数增大时,停止循环,具体算法如下,其中Pred(Xi)表示顺序在Xi之前的变量。
- 贪婪搜索
- CH评分衡量结构优劣性
- 利用结点序 ρ \rho ρ 以及正整数 μ \mu μ 来限制搜索空间的大小
结点序 ρ \rho ρ怎么确定?

P r e d ( V i ) Pred(V_i) Pred(Vi):根据节点顺序(node ordering)排在 V i V_i Vi前面的节点
K2算法由Kutato进化而来
爬山(hillclimbing)算法
爬山算法是一种简单的贪心搜索算法,该算法每次从当前解的临近解空间中选择一个最优解作为当前解,直到达到一个局部最优解。爬山算法实现很简单,其主要缺点是会陷入局部最优解,而不一定能搜索到全局最优解。假设C点为当前解,爬山算法搜索到A点这个局部最优解就会停止搜索,因为在A点无论向那个方向小幅度移动都不能得到更优的解。
- 局部操作(加边,减边,删边),评分高低作为是否选择该操作的标准。
- 通过贪婪选择来判断是否对模型结构进行更新。
# 爬山法伪代码
Procedure HillClimbing():old = getInitial() # get initial feasible solution xwhile(the stopping condition is not reached):for 加边,减边,删边 操作后的 newG: new= localSearch(N(x)); # select the optimal solution from the neighborhood of x as x'if(old <= new)old = newelsereturn oldend

爬山法
GES (greedy equivalent search)算法
- 从一个空图出发,采用两个不同的搜索阶段来寻找评分最高的结构。
- 采用贪心前向搜索法( GFS )来不断地在空图中加边,直至评分值无法提高为止;
- 利用贪心反向搜索法( greedy backward search, GBS)在图中不断地删除边,直至评分值不能提高为止。
基于约束|依赖统计
基于依赖统计分析的方法通常利用统计或信息论的方法分析变量间的依赖关系,从而获得最优的网络结构。而节点之间的依赖关系通常由两点的互信息或者条件互信息决定。
互信息
设 X i X_i Xi 、 X j X_j Xj 为 X 上的两个变量, x i x_i xi 、 x j x_j xj分别为变量 X i X_i Xi 、 X j X_j Xj 的取值,设 C 是 X 中非 X i X_i Xi 、 X j X_j Xj 变量组成的集合,则 X i X_i Xi 、 X j X_j Xj 关于 C 的条件互信息可以表示为:
3-1
I ( X i , X j ∣ C ) = ∑ x i , x j , c P ( x i , x j , c ) log P ( x i , x j , c ) P ( c ) P ( x i , c ) P ( x j , c ) I(X_i,X_j|C)=\sum_{x_i,x_j,c}P(x_i,x_j,c)\log\frac{P(x_i,x_j,c)P(c)}{P(x_i,c)P(x_j,c)} I(Xi,Xj∣C)=xi,xj,c∑P(xi,xj,c)logP(xi,c)P(xj,c)P(xi,xj,c)P(c)
I ( X i , X j ∣ C ) I(X_i,X_j|C) I(Xi,Xj∣C)的值越大,表示变量 X i X_i Xi 、 X j X_j Xj 关于C的依赖关系越大
I ( X i , X j ∣ C ) I(X_i,X_j|C) I(Xi,Xj∣C)小于设定的阈值 ξ \xi ξ,则表示 X i X_i Xi 、 X j X_j Xj 关于C条件独立,故3-1也可以表示节点之间的条件独立性测试
SGS 算法
是由 Spirtes 等人提出的一种典型的利用节点间条件独立性来确定网络结构的方法,算法利用特定的因果模型解决了统计意义的独立性不能适用于非测量性变量关系的问题,最终得出整个网络结构。
PC 算法
是在 SGS 算法的基础上,利用 稀疏网络 中节点不需要高阶独立性检验的特点,提出了一种削减策略:
依次由 0 阶独立性检验开始到高阶独立性检验,对初始网络中节点之间的连接进行削减。
此种策略有效地从稀疏模型中建立贝叶斯网络,解决了 SGS 算法随着网络中节点数的增长复杂度呈指数倍增长的问题。
TPDA 算法
为了进一步减少计算的复杂度,把结构学习过程分三个阶段进行:
- 起草(
drafting)网络结构,利用节点之间的互信息得到一个初始的网络结构; - 增厚(
thickening)网络结构,在 步骤1 网络结构的基础上计算网络中不存在连接节点间的条件互信息,对满足条件的两节点之间添加边; - 削减(
thinning)网络结构,计算 步骤2 网络结构中边的条件互信息,删除不满足条件的边。
现阶段对于基于依赖统计的方法的研究可分为基于分解的方法、基于 Markov blanket 的方法和基于结构空间限制的方法三种
基于分解
基于Markov blanket
基于空间结构限制
2. 不完备数据结构学习
- 所有评分函数无法分解成只与局部结构相关的因式
- 需要执行非线性的优化过程
- 为评判当前网络结构必须评估其所有的“邻居”
EM算法
- 高效地从不完整数据条件下学习网络参数,具有较高的精度。
- 一般般是收敛到局部最优结构。
SEM算法
- 只对当前选中的网络结构使用EM算法,进行概率分布评估;对于未被选中的网络并不使用EM算法。
- 每评价一个当前网络的“邻居”集,只调用一次EM算法,节省了计算开销
参考
贝叶斯网络结构学习(知乎)
2013 贝叶斯网络结构学习与推理研究 朱明敏
2015 贝叶斯网络结构学习综述 李硕豪
2017 贝叶斯网络结构学习与应用研究 曹杰